Lecture 2
1 Sampling
1.1 Sampling
- Sampling is widely used as a means of gathering useful information about a population.
- Data are gathered from samples and conclusions are drawn about the population as a part of the inferential statistics process.
- Often, a sample provides a reasonable means for gathering such useful decision-making information that might be otherwise unattainable and unaffordable.
- Sampling error occurs when the sample is not representative of the population.
1.2 Random versus non-random sampling
In random sampling every unit of the population has the same probability of being selected into the sample.
- Simple random sampling
- Stratified sampling
- Cluster sampling
- Multistage sampling
In non-random sampling not every unit of the population has the same probability of being selected into the sample.
- Convenience sampling
- Judgement sampling
- Quota sampling
1.3 Simple random sampling
Simple random sampling: is the basic sampling technique where we select a group of subjects (a sample) from a larger group (a population). Each individual is chosen entirely by chance and each member of the population has an equal chance of being included in the sample.
1.4 Central limit theorem
Let \(X_1, X_2, \ldots\) be independent and identically distributed (i.i.d.) random variables with mean \(\mu\) and variance \(\sigma^2\). Then as \(n\) increases indefinitely (i.e. \(n\rightarrow\infty\)), \(\overline{X}_n=\sum_{i=1}^{n}X_i/n\) approaches the normal distribution with mean \(\mu\) and variance \(\sigma^2/n\). That is \[\overline{X}_n \underset{n\rightarrow\infty}{\sim} N(\mu, \sigma^2/n)\]
Note that this result holds true regardless of the form of the underlying distribution. As a result, it follows that \[Z=\frac{\overline{X}_n-\mu}{\sigma/\sqrt{n}}\underset{n\rightarrow\infty}{\sim} N(0,1)\] That is, \(Z\) is a standardized normal variable.
1.5 Sampling distribution of the sample mean \(\bar{x}\)
The sampling distribution of a statistic is the probability distribution of that statistic.

There are two cases:
Sampling is from a normally distributed population with a known population variance: \[\bar{x}\sim N\left(\mu, \frac{\sigma^2}{n}\right) \] That is, the sampling distribution of the sample mean is normal with mean \(\mu_{\bar{x}}=\mu\) and standard deviation \(\sigma_{\bar{x}}=\sigma/\sqrt{n}\).
Sampling is from a non-normally distributed population with known population variance and \(n\) is large, then the mean of \(\bar{x}\), \[\mu_{\bar{x}}=\mu\] and the variance, \[\sigma^2_{\bar{x}}=\left\{\begin{array}{ll} \frac{\sigma^2}{n} & \text{with replacement (infinite population)}\\ &\\ \frac{\sigma^2}{n}\frac{N-n}{N-1} & \text{without replacement (finite population)} \end{array}\right.\]
If the sample size is large, the central limit theorem applies and the sampling distribution of \(\bar{x}\) will be approximately normal.
The standard deviation of the sampling distribution of the sample mean, \(\sigma_{\bar{x}}\), is called the standard error of the mean or, simply, the standard error
If \(\bar{x}\) is a normal distributed (or approximately normal distributed), we can use the following formula to transform \(\bar{x}\) to a \(Z\)-score.
\[Z=\frac{\bar{x}-\mu_{\bar{x}}}{\sigma_{\bar{x}}}\] where \(Z \sim N(0,1)\).
1.6 Sampling distribution of the sample proportion
When the sample size \(n\) is large, the distribution of the sample proportion, \(\hat{\pi}\), is approximately normally distributed by the use of the central limit theorem, \[\hat{\pi}\thickapprox N\left(\pi,\frac{\pi(1-\pi)}{n}\right)\] then \[Z=\frac{\hat{\pi}-\pi}{\sqrt{\frac{\pi(1-\pi)}{n}}}\thickapprox N(0,1)\] where \(\hat{\pi}=x/n\), \(x\) is the number in the sample with the characteristic of interest.
A widely used criterion is that both \(n\pi\) and \(n(1-\pi)\) must be greater than 5 for this approximation to be reasonable.
1.7 Sampling distribution of the sample variance
Sampling is from a normally distributed population with mean \(\mu\) and variance \(\sigma^2\). The sample variance is \[s^2=\frac{1}{n-1}\sum_{i=1}^{n} (x_i-\bar{x})^2\] and \[E(s^2)=\sigma^2\] \[Var(s^2)= 2\sigma^4/(n-1)\] Then \[\frac{(n-1)s^2}{\sigma^2}\sim \chi^2_{n-1}\]
1.8 Example
Suppose that during any hour in a large department store, the average number of shoppers is 448, with a standard deviation of 21 shoppers. What is the probability that a random sample of 49 different shopping hours will yield a sample mean between 441 and 446 shoppers?
\[\mu =448, \sigma=21, n=49\] \[\begin{align*} P(441\leq \bar{x} \leq 446)=&\left( \frac{441-448}{21/\sqrt{49}}\leq \frac{\bar{x}-\mu}{\sigma/\sqrt{n}}\leq \frac{446-448}{21/\sqrt{49}}\right)\\ P(-2.33 \leq Z \leq -0.67)=&P(Z \leq -0.67)-P(Z \leq -2.33)\\ =&0.2514-0.0099=0.2415 \end{align*}\]
 That is there is a 24.15% chance of randomly selecting 49 hourly periods for which the sample mean is between 441 and 446 shoppers.
That is there is a 24.15% chance of randomly selecting 49 hourly periods for which the sample mean is between 441 and 446 shoppers.
We used the standard normal table to obtain these probabilities. We can also use R.
pnorm(-0.67)-pnorm(-2.33)## [1] 0.24152582 Estimation
2.1 Estimation
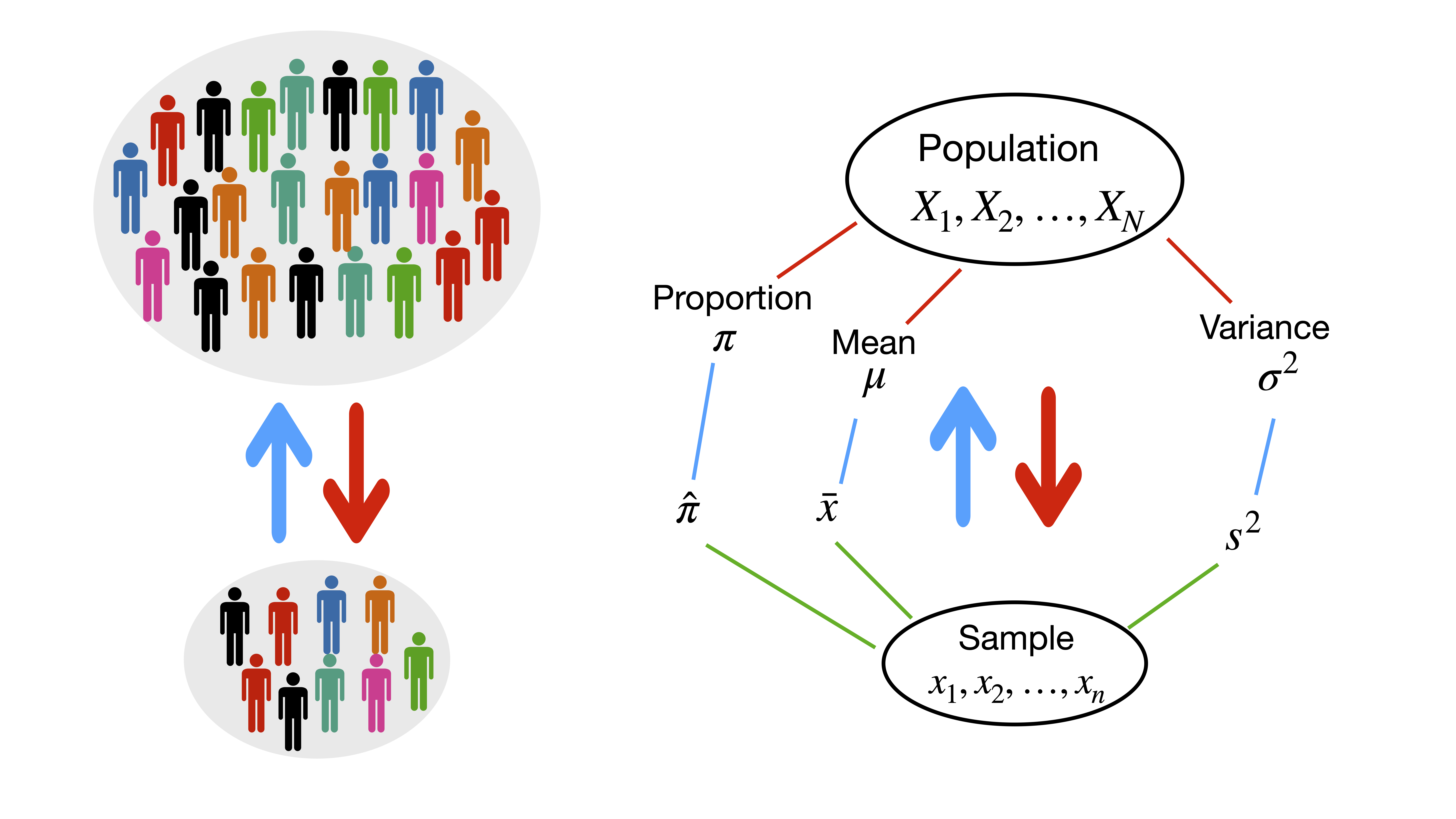
- The values of population parameters are often unknown.
- We use a representative sample of the population to estimate the population parameters.
There are two types of estimation:
- Point Estimation
- Interval Estimation
2.2 Point estimation
A point estimate is a single numerical value used to estimate the corresponding population parameter. A point estimate is obtained by selecting a suitable statistic (a suitable function of the data) and computing its value from the given sample data. The selected statistic is called the point estimator.
The point estimator is a random variable, so it has a distribution, mean, variance etc.
e.g. the sample mean \(\overline{X}=(1/n)\sum_{i=1}^{n}X_i\) is one possible point {} of the population mean \(\mu\), and the point estimate is \(\bar{x}=(1/n)\sum_{i=1}^{n}x_i\).
Properties:
Let \(\theta\) be the unknown population parameter and \(\hat{\theta}\) be its estimator. The parameter space is denoted by \(\Theta\).
An estimator \(\hat{\theta}\) is called unbiased estimator of \(\theta\) if \(E( \hat{\theta}) = \theta\).
The bias of the estimator \(\hat{\theta}\) is defined as \(Bias(\hat{\theta})=E(\hat{\theta})-\theta\)
Mean Square Error (MSE) is a measure of how close \(\hat{\theta}\) is, on average, to the true \(\theta\), \[MSE=E[(\hat{\theta}-\theta)^2]= Var(\hat{\theta}) + [Bias (\hat{\theta})]^2\]
2.3 Interval estimation
An interval estimate (confidence interval) is an interval, or range of values, used to estimate a population parameter.
The level of confidence \((1-\alpha)100\%\) is the probability that the interval estimate contains the population parameter.
Interval estimate components:
\[\text{point estimate}\; \pm \; (\text{critical value}\; \times\; \text{standard error})\]
2.4 Confidence intervals for the population mean
When sampling is from a normal distribution with known variance \(\sigma^2\), then a \(100(1-\alpha)\%\) confidence interval for the population mean \(\mu\) is \[ \bar{x}\pm z_{\alpha/2} \; (\sigma/\sqrt{n} )\] where \(z_{\alpha/2}\) can be obtained from the standard normal distribution table.
\(100(1-\alpha)\%\) \(\alpha\) \(z_{\alpha/2}\) \(90\%\) 0.10 1.645 \(95\%\) 0.05 1.96 \(99\%\) 0.01 2.58 If \(\sigma\) is unknown and \(n \geq 30\), the sample standard deviation \(s=\sqrt{\sum(x_i-\bar{x})^2/(n-1)}\) can be used in place of \(\sigma\).


If the sampling is from a non-normal distribution and \(n \geq 30\), then the sampling distribution of \(\bar{x}\) is approximately normally distributed (central limit theorem) and we can use the same formula, \(\bar{x}\pm z_{\alpha /2} \; (\sigma /\sqrt{n} )\), to construct the approximate confidence interval for population mean.
When sampling is from a normal distribution whose standard deviation \(\sigma\) is unknown and the sample size is small, the \(100(1-\alpha)\%\) confidence interval for the population mean \(\mu\) is \[ \bar{x}\pm t_{\alpha /2} \; (s /\sqrt{n} )\] where \(t_{\alpha/2}\) can be obtained from the \(t\) distribution table with \(df=n-1\) and \(s\) is the sample standard deviation which is given by \[s=\sqrt{\frac{\sum(x_i-\bar{x})^2}{n-1}}\]
If \(\sigma\) is unknown, and we neither have normal population nor large sample, then we should use nonparametric statistics (not cover in this course).
2.5 Interpreting confidence intervals
Probabilistic interpretation: In repeated sampling, from some population, \(100(1-\alpha)\%\) of all intervals which we constructed will in the long run include the population parameter.
Practical interpretation: When sampling is from some population, we have \(100(1-\alpha)\%\) confidence that the single computed interval contains the population parameter.
2.6 Confidence interval for a population proportion
The \(100(1-\alpha)\%\) confidence interval for a population proportion \(\pi\) is given by \[\hat{\pi}\pm z_{\alpha/2} \sqrt{\frac{\hat{\pi}(1-\hat{\pi})}{n}} \] where \(\hat{\pi}\) is the sample proportion.
2.7 Confidence interval for a population variance
The \(100(1-\alpha)\%\) confidence interval for the variance, \(\sigma^2\), of a normally distributed population is given by \[\left(\frac{(n-1)s^2}{\chi^2_{\frac{\alpha}{2}, n-1}}, \frac{(n-1)s^2}{\chi^2_{1-\frac{\alpha}{2}, n-1}}\right)\] where \(s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2\) is the sample variance.
2.8 Example
Suppose a car rental firm wants to estimate the average number of kilometres travelled per day by each of its cars rented in London. A random sample of 20 cars rented in London reveals that the sample mean travel distance per day is 85.5 kilometres, with a population standard deviation of 19.3 kilometres. Compute a 99% confidence interval to estimate \(\mu\).
For a 99% level of confidence, a \(z\) value of 2.58 is obtained (from the standard normal table). Assume that number of kilometres travelled per day is normally distributed.% in the population. \[\bar{x}\pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\] \[85.5 \pm 2.58 \frac{19.3}{\sqrt{20}}\] \[85.5 \pm 11.1\] \[\text{thus}\;\; 74.4 \leq \mu \leq 96.6\]
qnorm((1-0.99)/2)## [1] -2.5758293 Hypothesis Testing One Sample
3.1 Hypothesis testing: Motivation
We often encounter such statements or claims:
A newspaper claims that the average starting salary of MBA graduates is over 50K. (one sample test)
A claim about the efficiency of a particular diet program, the average weight after the program is less than the average weight before the program. (two paired samples test)
On average female managers earn less than male managers, given that they have the same qualifications and skills. (two independent samples test)
So we have claims about the populations’ means (averages) and we would like to verify or examine these claims.
This is a kind of problem that hypothesis testing is designed to solve.
3.2 The nature of hypothesis testing
We often use inferential statistics to make decisions or judgments about the value of a parameter, such as a population mean.
Typically, a hypothesis test involves two hypotheses:
- Null hypothesis: a hypothesis to be tested, denoted by \(H_0\).
- Alternative hypothesis (or research hypothesis): a hypothesis to be considered as an alternate to the null hypothesis, denoted by \(H_1\) or \(H_a\).
The problem in a hypothesis test is to decide whether or not the null hypothesis should be rejected in favour of the alternative hypothesis.
The choice of the alternative hypothesis should reflect the purpose of performing the hypothesis test.
How do we decide whether or not to reject the null hypothesis in favour of the alternative hypothesis?
Very roughly, the procedure for deciding is the following:
- Take a random sample from the population.
- If the sample data are consistent with the null hypothesis, then do not reject the null hypothesis; if the sample data are inconsistent with the null hypothesis, then reject the null hypothesis and conclude that the alternative hypothesis is true.
Test statistic: the statistic used as a basis for deciding whether the null hypothesis should be rejected.
The test statistic is a random variable which therefore has a sampling distribution with mean and standard deviation (so-called standard error).
3.3 Type I and Type II Errors

Type I error: rejecting the null hypothesis when it is in fact true.
Type II error: not rejecting the null hypothesis when it is fact false.
The significance level, \(\alpha\), of a hypothesis test is defined as the probability of making a Type I error, that is, the probability of rejecting a true null hypothesis.
Relation between Type I and II error probabilities: For a fixed sample size, the smaller the Type I error probability, \(\alpha\), of rejecting a true null hypothesis, the larger the Type II error probability of not rejecting a false null hypothesis and vice versa.
Possible conclusions for a hypothesis test: If the null hypothesis is rejected, we conclude that the alternative hypothesis is probably true. If the null hypothesis is not rejected, we conclude that the data do not provide sufficient evidence to support the alternative hypothesis.
When the null hypothesis is rejected in a hypothesis test performed at the significance level \(\alpha\), we say that the results are statistically significant at level \(\alpha\).
3.4 Hypothesis tests for one population mean
In order to test the hypothesis that the population mean \(\mu\) is equal to a particular value \(\mu_0\), we are going to test the null hypothesis
\[H_0:\mu=\mu_0\]
against one of the following alternatives:
- \(H_1:\mu\neq\mu_0\) (Two-tailed)
- \(H_1:\mu<\mu_0\) (Left-tailed)
- \(H_1:\mu>\mu_0\) (Right-tailed)
In order to test \(H_0\), we need to use one of the following test statistics, we should choose the one that satisfies the assumptions.
- If \(\sigma\) is known, and we have a normally distributed population or large sample (\(n\geq 30\)), then the test statistic, so-called \(z\)-test, is \[z=\frac{\bar{x}-\mu_0}{\sigma / \sqrt{n}}\] where \(\sigma\) is the standard deviation of the population.
- If \(\sigma\) is unknown, and we have a normally distributed population or large sample (\(n \geq 30\)), then the test statistic, so-called \(t\)-test, is \[t=\frac{\bar{x}-\mu_0}{s/\sqrt{n}}\;\;\text{with}\;\; df=n-1.\] where \(s\) is the standard deviation of the sample.
3.5 The \(p\)-value approach to hypothesis testing
The \(p\text{-value}\) is the smallest significance level at which the null hypothesis would be rejected. The \(p\)-value is also known as the observed significance level.
The \(p\text{-value}\) measures how well the observed sample agrees with the null hypothesis. A small \(p\text{-value}\) (close to zero) indicates that the sample is not consistent with the null hypothesis and the null hypothesis should be rejected. On the other hand, a large \(p\text{-value}\) (larger than 0.10) generally indicates a reasonable level of agreement between the sample and the null hypothesis.
As a rule of thumb, if \(p \text{-value} \leq \alpha\) then reject \(H_0\); otherwise do not reject \(H_0\).
3.6 Critical-value approach to hypothesis testing
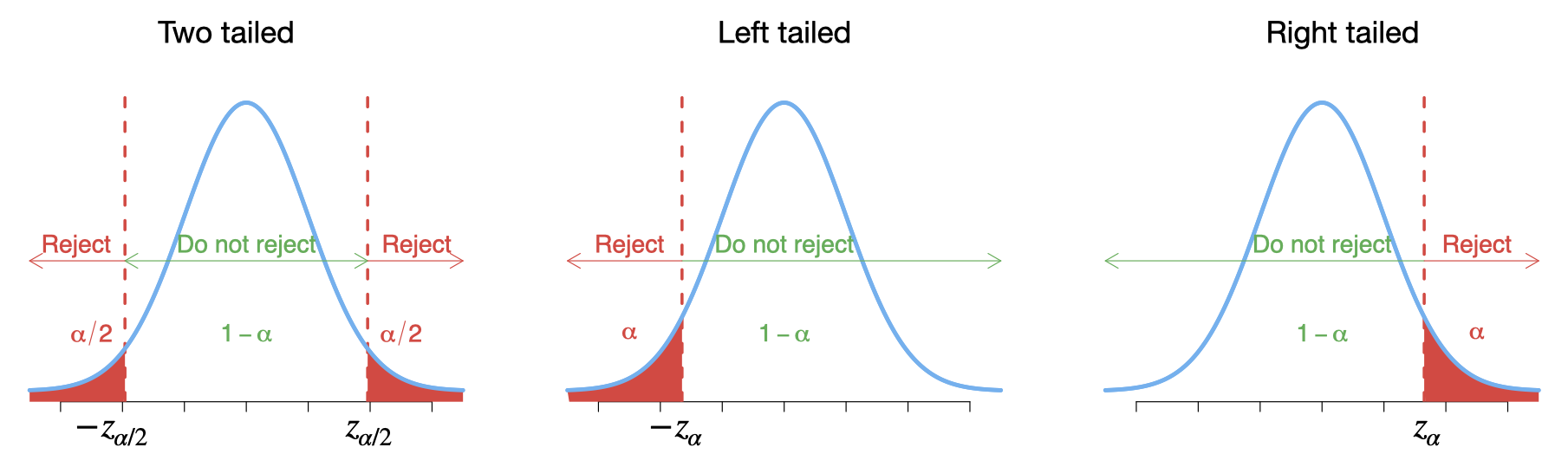
For any specific significance level \(\alpha\), one can obtain these critical values \(\pm z_{\alpha/2}\) and \(\pm z_{\alpha}\) from the standard normal table.
| 1.282 | 1.645 | 1.960 | 2.326 | 2.576 |
|---|---|---|---|---|
| \(z_{0.10}\) | \(z_{0.05}\) | \(z_{0.025}\) | \(z_{0.01}\) | \(z_{0.005}\) |
If the value of the test statistic falls in the rejection region, reject \(H_0\); otherwise do not reject \(H_0\).
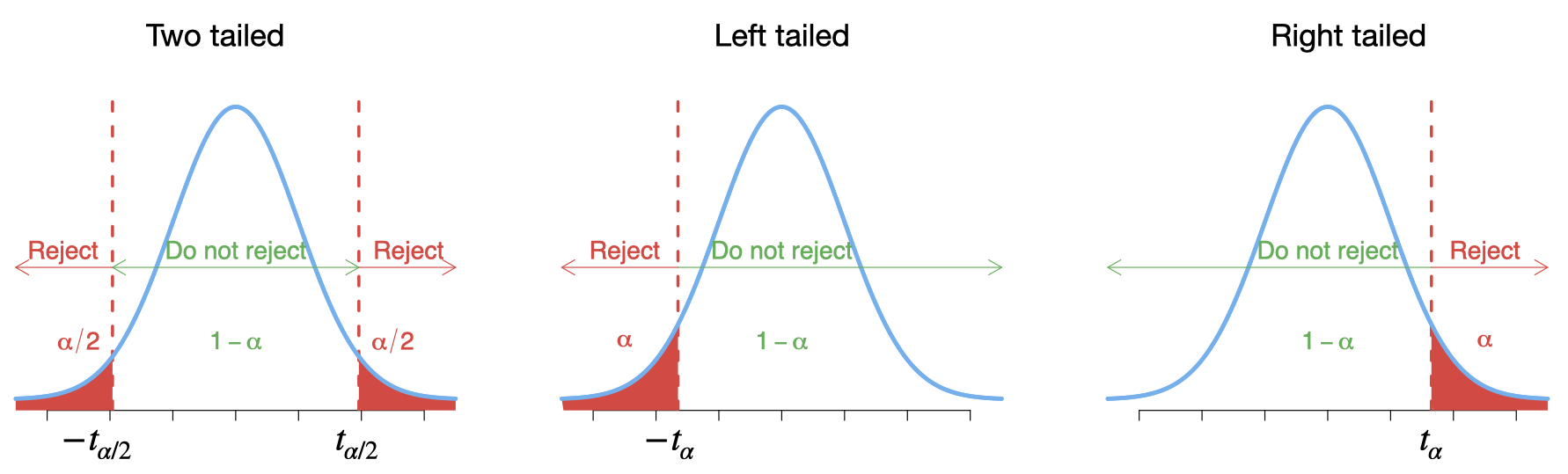
For any specific significance level \(\alpha\), one can obtain these critical values \(\pm t_{\alpha/2}\) and \(\pm t_{\alpha}\) from the T distribution table. For example, for \(df=9\) and \(\alpha=.05\), the critical values are \(\pm t_{0.025}=\pm 2.262\) and \(\pm t_{0.05}=\pm 1.833\).
3.7 Hypothesis testing and confidence intervals
Hypothesis tests and confidence intervals are closely related. Consider, for instance, a two tailed hypothesis test for a population mean at the significance level \(\alpha\). It can be shown that the null hypothesis will be rejected if and only if the value \(\mu_0\) given for the mean in the null hypothesis lies outside the 100(\(1-\alpha\))-level confidence interval for \(\mu\).
Example:
- At significance level \(\alpha=0.05\), we want to test \(H_0: \mu = 40\) against \(H_1: \mu \neq 40\) (so here \(\mu_0=40\)).
- Suppose that the 95% confidence interval for \(\mu\) is \(35<\hspace{-1mm}\mu\hspace{-1mm}<38\).
- As \(\mu_0=40\) lies outside this confidence intervals, we reject \(H_0\).
3.8 Test of Normality
One of the assumptions in order to use \(z\)-test or \(t\)-test is that the population which we sampled from is normally distributed. However we did not yet test this assumption, we should perform a so-called test of normality. In order to do so:
We can plot our data sample, e.g. histogram, boxplot, stem-and-leaf and normal Q-Q plot
Use normality tests such as Kolmogorov-Smirnov test or Shapiro-Wilk test. The null and alternative hypotheses are:
- \(H_0\): the population being sampled is normally distributed.
- \(H_1\): the population being sampled is nonnormally distributed.
If \(\sigma\) is unknown, and we neither have normal population nor large sample, then we should use nonparametric tests instead of \(z\)-test or \(t\)-test (not cover in this course).
3.9 Example
A company reported that a new car model equipped with an enhanced manual transmission averaged 29 mpg on the highway. Suppose the Environmental Protection Agency tested 15 of the cars and obtained the following gas mileages.
| 27.3 | 30.9 | 25.9 | 31.2 | 29.7 |
| 28.8 | 29.4 | 28.5 | 28.9 | 31.6 |
| 27.8 | 27.8 | 28.6 | 27.3 | 27.6 |
What decision would you make regarding the company’s claim on the gas mileage of the car? Perform the required hypothesis test at the 5% significance level.
Solution:
The null and alternative hypotheses: \[H_0: \mu =29 \;\text{mpg vs.}\;\;\; H_1: \mu \neq 29\; \text{mpg} \] The value of the test statistic, \[ t=\frac{\bar{x}-\mu _{0} }{s/\sqrt{n} }=\frac{28.753-29}{1.595/\sqrt{15}} =-0.599\] As \(p\)-value \(= 0.559 > \alpha = 0.05\). So, we cannot reject \(H_0\). At the \(5\%\) significance level, the data do not provide sufficient evidence to conclude that the company’s report was incorrect.

R output:
# Data
mlg<-c(27.3, 30.9, 25.9, 31.2, 29.7,
28.8, 29.4, 28.5, 28.9, 31.6,
27.8, 27.8, 28.6, 27.3, 27.6)
# t-test
t.test(mlg,alternative = "two.sided", mu = 29, conf.level = 0.95)##
## One Sample t-test
##
## data: mlg
## t = -0.59878, df = 14, p-value = 0.5589
## alternative hypothesis: true mean is not equal to 29
## 95 percent confidence interval:
## 27.86979 29.63688
## sample estimates:
## mean of x
## 28.75333# Normality test
# Kolmogorov Smirnov Test
ks.test(mlg,"pnorm", mean=mean(mlg), sd=sd(mlg))## Warning in ks.test(mlg, "pnorm", mean = mean(mlg), sd = sd(mlg)): ties should
## not be present for the Kolmogorov-Smirnov test##
## One-sample Kolmogorov-Smirnov test
##
## data: mlg
## D = 0.13004, p-value = 0.9616
## alternative hypothesis: two-sided# Shapiro-Wilk test
shapiro.test(mlg) ##
## Shapiro-Wilk normality test
##
## data: mlg
## W = 0.95817, p-value = 0.6606par(mfrow=c(1,2))
qqnorm(mlg)
qqline(mlg, col = "red")
hist(mlg)
4 Hypothesis Testing Two Samples (Workshop 3)
4.1 Motivation
We often encounter such statements or claims:
A newspaper claims that the average starting salary of MBA graduates is over 50K. (one sample test)
A claim about the efficiency of a particular diet program, the average weight after the program is less than the average weight before the program. (two paired samples test)
On average female managers earn less than male managers, given that they have the same qualifications and skills. (two independent samples test)
So we have claims about the populations’ means (averages) and we would like to verify or examine these claims.
This is a kind of problem that hypothesis testing is designed to solve.
4.2 Hypothesis tests for two population means
We have two types of samples here:
Paired samples: each case must have scores on two variables and it is applicable to two types of studies, repeated-measures (e.g. weights before and after a diet plan) and matched-subjects designs (e.g. measurements on twins or child/parent pairs).
Independent samples: two samples are called independent samples if the sample selected from one of the populations has no effect on (holds no information about) the sample selected from the other population.
4.3 Hypothesis tests for two population means
In order to compare two population means, we are going to test the null hypothesis \[H_{0} :\mu _{1} =\mu _{2} \]
against one of the following alternatives:
\(H_1:\mu_1\neq\mu_2\;\) or \(\;\mu_1-\mu_2\neq 0\) (Two-tailed)
\(H_1:\mu_1<\mu_2\;\) or \(\;\mu_1-\mu_2< 0\) (Left-tailed)
\(H_1:\mu_1>\mu_2\;\) or \(\;\mu_1-\mu_2> 0\) (Right-tailed)
4.5 Comparing two means: Independent samples
In order to test \(H_0:\mu_1=\mu_2\) for two independent samples, we need to use one of the following test statistics, we should choose the one that satisfies the assumptions. Let \(\sigma_1\) and \(\sigma_2\) be the standard deviations of population 1 and population 2, respectively.
4.5.1 z-test
Assumptions: \(\sigma_1\) and \(\sigma_2\) are known and we have large samples (\(n_1\geq30\), \(n_2\geq30\))
Test statistic: z-test \[z=\frac{\bar{x}_{1} -\bar{x}_{2} }{\sqrt{(\sigma_1^2 /n_1 )+(\sigma_2^2 /n_2 )} } \]
\(100(1- \alpha)\%\) confidence intervals for the difference between two population means \(\mu_{1} -\mu_{2}\) are \[(\bar{x}_{1} -\bar{x}_{2} )\pm z_{\alpha /2} \; \sqrt{(\sigma_{1}^{2} /n_{1} )+(\sigma_{2}^{2} /n_{2} )} \]
where \(z_{\alpha/2}\) is the \(\alpha/2\) critical value from the standard normal distribution.
4.5.2 Pooled t-test
Assumptions: Normal populations, \(\sigma_1\) and \(\sigma_2\) are unknown but equal (\(\sigma_1 = \sigma_2\))
Test statistic: Pooled t-test \[t=\frac{\bar{x}_{1} -\bar{x}_{2} }{s_{p} \; \sqrt{(1/n_{1} )+(1/n_{2} )} } \] has a t-distribution with \(df=n_{1} +n_{2} -2\), where \(s_{p} =\sqrt{\frac{(n_{1} -1)s_{1}^{2} +(n_{2} -1)s_{2}^{2} }{n_{1} +n_{2} -2} }\).
\(100(1- \alpha)\%\) confidence intervals for the difference between two population means \(\mu_{1} -\mu_{2}\) are \[(\bar{x}_{1} -\bar{x}_{2} )\pm t_{\alpha /2} \; s_{p} \sqrt{(1/n_{1} )+(1/n_{2} )} \] where \(t_{\alpha/2}\) is the \(\alpha/2\) critical value from the t-distribution with \(df=n_{1} +n_{2} -2\).
4.5.3 Non-Pooled t-test
Assumptions: Normal populations, \(\sigma_1\) and \(\sigma_2\) are unknown and unequal (\(\sigma_1 \neq \sigma_2\))
Test statistic: Non-Pooled t-test \[t=\frac{\bar{x}_{1} -\bar{x}_{2} }{\sqrt{(s_{1}^{2} /n_{1} )+(s_{2}^{2} /n_{2} )} } \] has a t-distribution with \(\displaystyle df=\Delta=\frac{[(s_{1}^{2} /n_{1} )+(s_{2}^{2} /n_{2} )]^{2} }{\left[\frac{(s_{1}^{2} /n_{1} )^{2} }{n_{1} -1} +\frac{(s_{2}^{2} /n_{2} )^{2} }{n_{2} -1} \right]}\)
100(1- \(\alpha\))% confidence intervals for the difference between two population means \(\mu_{1} -\mu_{2}\) are \[(\bar{x}_{1} -\bar{x}_{2} )\pm t_{\alpha /2} \; \sqrt{(s_{1}^{2} /n_{1} )+(s_{2}^{2} /n_{2} )} \] where \(t_{\alpha/2}\) is the \(\alpha/2\) critical value from the t-distribution with \(df =\Delta\).
4.5.4 Levene’s Test for Equality of Variances
In order to choose between Pooled t-test and Non-Pooled t-test, we need to check the assumption that the two populations have equal (but unknown) variances. That is, test the null hypothesis that \(H_0:\sigma^2_1=\sigma^2_2\) against the alternative that \(H_1:\sigma^2_1\neq \sigma^2_2\).
The test statistic of Levene’s test follows \(F\) distribution with \(1\) and \(n_1+n_2-2\) degrees of freedoms.

4.6 Critical-value approach to hypothesis testing

For any specific significance level \(\alpha\), one can obtain these critical values \(\pm z_{\alpha/2}\) and \(\pm z_{\alpha}\) from the standard normal distribution table. If the value of the test statistic falls in the rejection region, reject \(H_0\); otherwise do not reject \(H_0\).
| \(z_{0.10}\) | \(z_{0.05}\) | \(z_{0.025}\) | \(z_{0.01}\) | \(z_{0.005}\) |
|---|---|---|---|---|
| 1.282 | 1.645 | 1.96 | 0 | 2.326 2.576 |
4.7 Critical-value approach to hypothesis testing

For any specific significance level \(\alpha\), one can obtain these critical values \(\pm t_{\alpha/2}\) and \(\pm t_{\alpha}\) from the T distribution table. For example, for \(df=9\) and \(\alpha=.05\), the critical values are \(\pm t_{0.025}=\pm 2.262\) and \(\pm t_{0.05}=\pm 1.833\).
4.8 Critical-value approach to hypothesis testing
State the null and alternative hypotheses
Decide on the significance level \(\alpha\)
Compute the value of the test statistic
Determine the critical value(s)
If the value of the test statistic falls in the rejection region, reject \(H_0\); otherwise do not reject \(H_0\).
Interpret the result of the hypothesis test.
We can replace Steps 4 and 5 by using the p-value. A common rule of thumb is that we reject the null hypothesis if the p-value is less than or equal to the significance level \(\alpha\).
4.9 Example
In a study of the effect of cigarette smoking on blood clotting, blood samples were gathered from 11 individuals before and after smoking a cigarette and the level of platelet aggregation in the blood was measured. Does smoking affect platelet aggregation?
| before | after | d |
|---|---|---|
| 25 | 27 | 2 |
| 25 | 29 | 4 |
| 27 | 37 | 10 |
| 44 | 56 | 12 |
| 30 | 46 | 16 |
| 67 | 82 | 15 |
| 53 | 57 | 4 |
| 53 | 80 | 27 |
| 52 | 61 | 9 |
| 60 | 59 | -1 |
| 28 | 43 | 15 |
\[\bar{d}=\frac{1}{n}\sum_{i=1}^nd_i=10.27\] \[s_d=7.98\] \[s_{\bar{d}}=\frac{s_d}{\sqrt{n}}=\frac{7.98}{\sqrt{11}}=2.40\]
At the 90% level (\(\alpha=0.10\)), the critical value \(t_{10,0.05}=1.812\), and so a 90% confidence interval is
\[\bar{d}\pm 1.812\;(s_d/\sqrt{n})=10.27\pm1.812\times 2.40=[5.19,14.63]\]
which clearly excludes 0.
To test the null hypothesis that the means before and after are the sample: that is \(H_0:\mu_{before}=\mu_{after}\) against \(H_1:\mu_{before}\neq\mu_{after}\) \[t=\frac{\bar{d}}{s_d/\sqrt{n}}=\frac{10.27}{2.40}=4.28\] since \(|t|>1.812\) then we reject \(H_0\).

before<-c(25,25,27,44,30,67,53,53,52,60,28)
after<-c(27,29,37,56,46,82,57,80,61,59,43)
d<-after-before
qt(0.1/2, df=10)## [1] -1.812461t.test(after, before, "two.sided", paired = TRUE,conf.level = 0.90)##
## Paired t-test
##
## data: after and before
## t = 4.2716, df = 10, p-value = 0.001633
## alternative hypothesis: true difference in means is not equal to 0
## 90 percent confidence interval:
## 5.913967 14.631488
## sample estimates:
## mean of the differences
## 10.27273hist(d,main="",col = '#61B2F2')
qqnorm(d, pch = 1)
qqline(d, col = "steelblue", lwd = 2)