Workshop 6
This workshop is based on Chapters 2 and 3 from the ISL book. James, Witten, Hastie, and Tibshirani (2013). An Introduction to Statistical Learning: with Applications in R.
To start, create a new R script by clicking on the corresponding menu button (in the top left); and save it somewhere in your computer. You can now write all your code into this file, and then execute it in R using the menu button Run or by simple pressing ctrl \(+\) enter.
1 Boston Housing Data
In this workshop, we will use the Boston data set (from the MASS package), which consists of 506 observations concerning housing values in the area of Boston. We are interested in predicting the median house value medv using the 13 predictor variables; such as crim (per capita crime rate by town), rm (average number of rooms per house), age (average age of houses), and lstat (percent of households with low socioeconomic status).
\(~\)
First, we need to install the MASS package, using the command install.packages("MASS"). We only need to do this once.
Now, load the package and the data set:
library(MASS)
data("Boston")
attach(Boston)1.1 Exploratory data analysis
To get more information about the data set:
names(Boston)## [1] "crim" "zn" "indus" "chas" "nox" "rm" "age"
## [8] "dis" "rad" "tax" "ptratio" "black" "lstat" "medv"?Boston
str(Boston)## 'data.frame': 506 obs. of 14 variables:
## $ crim : num 0.00632 0.02731 0.02729 0.03237 0.06905 ...
## $ zn : num 18 0 0 0 0 0 12.5 12.5 12.5 12.5 ...
## $ indus : num 2.31 7.07 7.07 2.18 2.18 2.18 7.87 7.87 7.87 7.87 ...
## $ chas : int 0 0 0 0 0 0 0 0 0 0 ...
## $ nox : num 0.538 0.469 0.469 0.458 0.458 0.458 0.524 0.524 0.524 0.524 ...
## $ rm : num 6.58 6.42 7.18 7 7.15 ...
## $ age : num 65.2 78.9 61.1 45.8 54.2 58.7 66.6 96.1 100 85.9 ...
## $ dis : num 4.09 4.97 4.97 6.06 6.06 ...
## $ rad : int 1 2 2 3 3 3 5 5 5 5 ...
## $ tax : num 296 242 242 222 222 222 311 311 311 311 ...
## $ ptratio: num 15.3 17.8 17.8 18.7 18.7 18.7 15.2 15.2 15.2 15.2 ...
## $ black : num 397 397 393 395 397 ...
## $ lstat : num 4.98 9.14 4.03 2.94 5.33 ...
## $ medv : num 24 21.6 34.7 33.4 36.2 28.7 22.9 27.1 16.5 18.9 ...# Look at the first few rows
head(Boston)## crim zn indus chas nox rm age dis rad tax ptratio black lstat
## 1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
## 2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
## 3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
## 4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
## 5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33
## 6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21
## medv
## 1 24.0
## 2 21.6
## 3 34.7
## 4 33.4
## 5 36.2
## 6 28.7# Summary statistics
summary(Boston)## crim zn indus chas
## Min. : 0.00632 Min. : 0.00 Min. : 0.46 Min. :0.00000
## 1st Qu.: 0.08205 1st Qu.: 0.00 1st Qu.: 5.19 1st Qu.:0.00000
## Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.00000
## Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.06917
## 3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.00000
## Max. :88.97620 Max. :100.00 Max. :27.74 Max. :1.00000
## nox rm age dis
## Min. :0.3850 Min. :3.561 Min. : 2.90 Min. : 1.130
## 1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100
## Median :0.5380 Median :6.208 Median : 77.50 Median : 3.207
## Mean :0.5547 Mean :6.285 Mean : 68.57 Mean : 3.795
## 3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188
## Max. :0.8710 Max. :8.780 Max. :100.00 Max. :12.127
## rad tax ptratio black
## Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
## 1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38
## Median : 5.000 Median :330.0 Median :19.05 Median :391.44
## Mean : 9.549 Mean :408.2 Mean :18.46 Mean :356.67
## 3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23
## Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
## lstat medv
## Min. : 1.73 Min. : 5.00
## 1st Qu.: 6.95 1st Qu.:17.02
## Median :11.36 Median :21.20
## Mean :12.65 Mean :22.53
## 3rd Qu.:16.95 3rd Qu.:25.00
## Max. :37.97 Max. :50.00# Check for missing values
sum(is.na(Boston))## [1] 0# zero here, so no missing values\(~\)
The following exercise is Question 10, Chapter 2, from the ISL book.
- How many rows are in this data set? How many columns? What do the rows and columns represent?
- Make some pairwise scatterplots of the predictors (columns) in this data set. Describe your findings.
- Are any of the predictors associated with per capita crime rate? If so, explain the relationship.
Click for solution
## SOLUTION
# (a)
dim(Boston)## [1] 506 14# 506 observations and 14 variables
# (b)
pairs(Boston)
# A nicer plot using the corrplot package.
#install.packages("corrplot")
library(corrplot)## corrplot 0.84 loaded#checking correlation between variables
corrplot(cor(Boston), method = "number", type = "upper", diag = FALSE)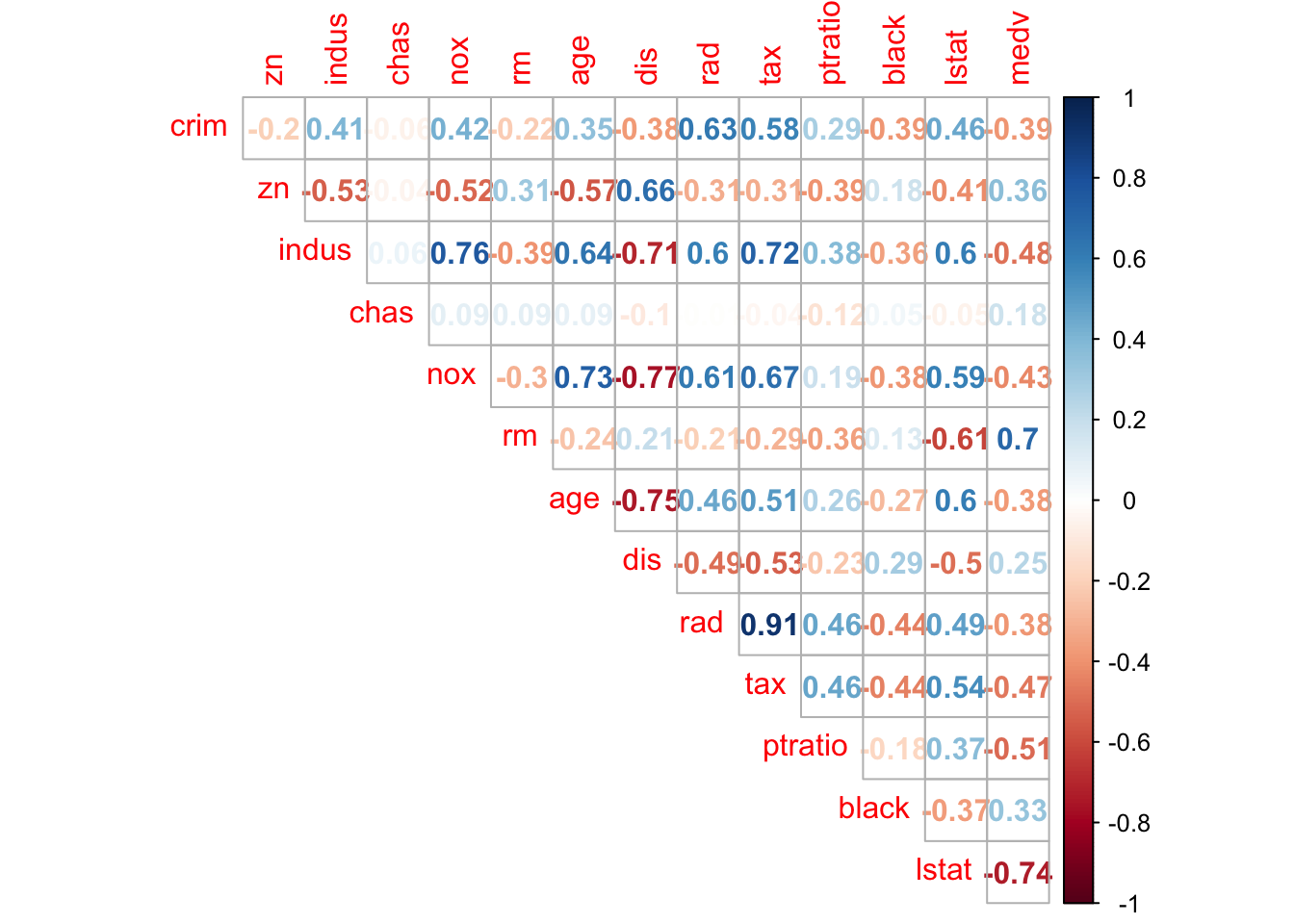
corrplot.mixed(cor(Boston), upper = "ellipse", lower = "number",number.cex = .7)
\(~\)
2 Simple Linear Regression
This section is based on Lab 3.6, pages 109-119, from the ISL book. For more information, see Workshop 5 or Linear regression.
2.1 Linear regression model fitting
- Use the
lm()function to fit a simple linear regression model, withmedvas the response variable andlstatas the predictor variable. Save the result of the regression function toreg1. - Use
summary(reg1)command to get information about the model. This gives us the estimated coefficients, t-tests, p-values and standard errors as well as the R-square and F-statistic for the model. - Use
names(reg1)function to find what types of information are stored inreg1. For example, we can get or extract the estimated coefficients using the functioncoef(reg1)orreg1$coefficients.
Click for solution
## SOLUTION
# (a)
reg1 <- lm(medv~lstat,data=Boston)
# (b)
summary(reg1)##
## Call:
## lm(formula = medv ~ lstat, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.168 -3.990 -1.318 2.034 24.500
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.55384 0.56263 61.41 <0.0000000000000002 ***
## lstat -0.95005 0.03873 -24.53 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.216 on 504 degrees of freedom
## Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
## F-statistic: 601.6 on 1 and 504 DF, p-value: < 0.00000000000000022# (c)
names(reg1)## [1] "coefficients" "residuals" "effects" "rank"
## [5] "fitted.values" "assign" "qr" "df.residual"
## [9] "xlevels" "call" "terms" "model"coef(reg1)## (Intercept) lstat
## 34.5538409 -0.9500494reg1$coefficients## (Intercept) lstat
## 34.5538409 -0.9500494\(~\)
2.2 Confidence and prediction intervals
- Obtain a 95% confidence interval for the coefficient estimates. Hint: use the
confint()command. - Obtain a 95% confidence and prediction intervals of
medvfor a given value oflstat. Assume this given value oflstatis equal to 10.
Click for solution
## SOLUTION
# (a)
confint(reg1, level = 0.95)## 2.5 % 97.5 %
## (Intercept) 33.448457 35.6592247
## lstat -1.026148 -0.8739505# (b)
newdata= data.frame(lstat=10)
predict(reg1,newdata=newdata, interval="confidence", level = 0.95)## fit lwr upr
## 1 25.05335 24.47413 25.63256predict(reg1,data.frame(lstat=10), interval="prediction", level = 0.95)## fit lwr upr
## 1 25.05335 12.82763 37.27907\(~\)
2.3 Regression diagnostics
- Create a scatterplot of
lstatandmedv. Is there a relationship between the two variables? - Plot
medvandlstatalong with the least squares regression line using theplot()andabline()functions. - Use residual plots to check the assumptions of the model.
Click for solution
## SOLUTION
# (a) & (b)
plot(lstat,medv, pch=16, col="cornflowerblue")
abline(reg1,lwd=3,col="red")
# (c)
par(mfrow=c(1,2)) # to have two plots side-by-side
plot(reg1, which=1, pch=16, col="cornflowerblue")
plot(reg1, which=2, pch=16, col="cornflowerblue")
par(mfrow=c(1,1)) # to return to one plot per window
par(mfrow=c(2,2))
plot(reg1, pch=16, col="green")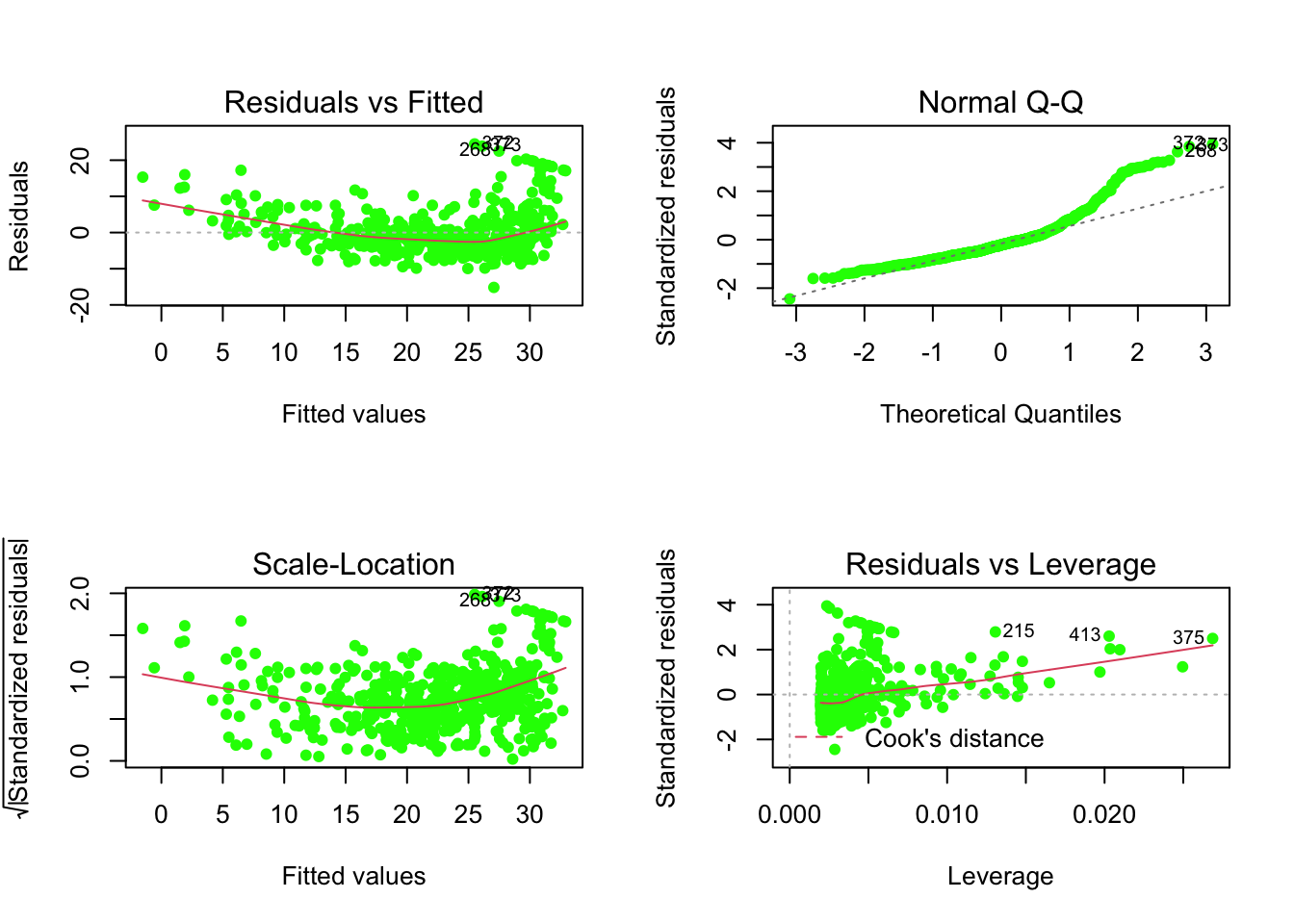
par(mfrow=c(1,1))\(~\)
3 Multiple Linear Regression
3.1 Linear regression model fitting
- Use the
lm()function again to fit a linear regression model, withmedvas the response variable and bothlstatandageas predictors. Save the result of the regression function toreg2. - Now use the
lm()function again to fit a linear regression model, withmedvas the response variable and all other 13 variables as predictors. Save the result of the regression function toreg3. Hint: Uselm(medv~., data=Boston). - Fit the same linear regression as in (b) but now exclude the age. Save the result of the regression function to
reg4. Hint: Uselm(medv~.-age, data=Boston). - Compare the R-squares of these models. Notice we can extract the R-square value from the summary object as
summary(reg)$r.sq. Type?summary.lmto see what else is available. - Use Variance Inflation Factor (VIF) to assess if there is any relationship between the independent variables. Hint: use the
vif()function from thecarpackage.
Click for solution
## SOLUTION
# (a)
reg2 <- lm(medv~lstat+age,data=Boston)
summary(reg2)##
## Call:
## lm(formula = medv ~ lstat + age, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.981 -3.978 -1.283 1.968 23.158
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 33.22276 0.73085 45.458 < 0.0000000000000002 ***
## lstat -1.03207 0.04819 -21.416 < 0.0000000000000002 ***
## age 0.03454 0.01223 2.826 0.00491 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.173 on 503 degrees of freedom
## Multiple R-squared: 0.5513, Adjusted R-squared: 0.5495
## F-statistic: 309 on 2 and 503 DF, p-value: < 0.00000000000000022# (b)
reg3 <- lm(medv~.,data=Boston)
summary(reg3)##
## Call:
## lm(formula = medv ~ ., data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.595 -2.730 -0.518 1.777 26.199
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.4594884 5.1034588 7.144 0.000000000003283 ***
## crim -0.1080114 0.0328650 -3.287 0.001087 **
## zn 0.0464205 0.0137275 3.382 0.000778 ***
## indus 0.0205586 0.0614957 0.334 0.738288
## chas 2.6867338 0.8615798 3.118 0.001925 **
## nox -17.7666112 3.8197437 -4.651 0.000004245643808 ***
## rm 3.8098652 0.4179253 9.116 < 0.0000000000000002 ***
## age 0.0006922 0.0132098 0.052 0.958229
## dis -1.4755668 0.1994547 -7.398 0.000000000000601 ***
## rad 0.3060495 0.0663464 4.613 0.000005070529023 ***
## tax -0.0123346 0.0037605 -3.280 0.001112 **
## ptratio -0.9527472 0.1308268 -7.283 0.000000000001309 ***
## black 0.0093117 0.0026860 3.467 0.000573 ***
## lstat -0.5247584 0.0507153 -10.347 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.745 on 492 degrees of freedom
## Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
## F-statistic: 108.1 on 13 and 492 DF, p-value: < 0.00000000000000022# (c)
reg4 <- lm(medv~.-age,data=Boston)
summary(reg4)##
## Call:
## lm(formula = medv ~ . - age, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.6054 -2.7313 -0.5188 1.7601 26.2243
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.436927 5.080119 7.172 0.0000000000027155 ***
## crim -0.108006 0.032832 -3.290 0.001075 **
## zn 0.046334 0.013613 3.404 0.000719 ***
## indus 0.020562 0.061433 0.335 0.737989
## chas 2.689026 0.859598 3.128 0.001863 **
## nox -17.713540 3.679308 -4.814 0.0000019671100076 ***
## rm 3.814394 0.408480 9.338 < 0.0000000000000002 ***
## dis -1.478612 0.190611 -7.757 0.0000000000000503 ***
## rad 0.305786 0.066089 4.627 0.0000047505389684 ***
## tax -0.012329 0.003755 -3.283 0.001099 **
## ptratio -0.952211 0.130294 -7.308 0.0000000000010992 ***
## black 0.009321 0.002678 3.481 0.000544 ***
## lstat -0.523852 0.047625 -10.999 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.74 on 493 degrees of freedom
## Multiple R-squared: 0.7406, Adjusted R-squared: 0.7343
## F-statistic: 117.3 on 12 and 493 DF, p-value: < 0.00000000000000022# (d)
summary(reg1)$r.sq## [1] 0.5441463summary(reg2)$r.sq## [1] 0.5512689summary(reg3)$r.sq## [1] 0.7406427summary(reg4)$r.sq## [1] 0.7406412summary(reg4)$r.squared## [1] 0.7406412# or the adjusted R Squared
summary(reg4)$adj.r.squared## [1] 0.7343282# (e)
#install.packages("car") # you need to do this once
library(car)
vif(reg3)## crim zn indus chas nox rm age dis
## 1.792192 2.298758 3.991596 1.073995 4.393720 1.933744 3.100826 3.955945
## rad tax ptratio black lstat
## 7.484496 9.008554 1.799084 1.348521 2.941491\(~\)
If you have time left, you can try the following:
\(~\)
3.2 Interaction between variables
It is straightforward to include the interaction between variables in the linear model using the lm() function. For example, the syntax lstat*age will include lstat, age and the interaction term lstat x age as predictors.
summary(lm(medv~lstat*age, data=Boston))##
## Call:
## lm(formula = medv ~ lstat * age, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.806 -4.045 -1.333 2.085 27.552
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.0885359 1.4698355 24.553 < 0.0000000000000002 ***
## lstat -1.3921168 0.1674555 -8.313 0.000000000000000878 ***
## age -0.0007209 0.0198792 -0.036 0.9711
## lstat:age 0.0041560 0.0018518 2.244 0.0252 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.149 on 502 degrees of freedom
## Multiple R-squared: 0.5557, Adjusted R-squared: 0.5531
## F-statistic: 209.3 on 3 and 502 DF, p-value: < 0.00000000000000022We can also include a non-linear transformation of the predictors, using the function I(). For example, we can regress the response variable medv on both lstat and lstat^2 as follows.
summary(lm(medv~lstat+I(lstat^2), data=Boston))##
## Call:
## lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.2834 -3.8313 -0.5295 2.3095 25.4148
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 42.862007 0.872084 49.15 <0.0000000000000002 ***
## lstat -2.332821 0.123803 -18.84 <0.0000000000000002 ***
## I(lstat^2) 0.043547 0.003745 11.63 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.524 on 503 degrees of freedom
## Multiple R-squared: 0.6407, Adjusted R-squared: 0.6393
## F-statistic: 448.5 on 2 and 503 DF, p-value: < 0.00000000000000022If we are interested in a higher-order polynomial then it is best to use the poly() function within the lm() function. For example, we use the command below if we are interested in the fifth-order polynomial fit of the lstat, where again the medv is the response variable.
summary(lm(medv~poly(lstat,5), data=Boston))##
## Call:
## lm(formula = medv ~ poly(lstat, 5), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.5433 -3.1039 -0.7052 2.0844 27.1153
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.5328 0.2318 97.197 < 0.0000000000000002 ***
## poly(lstat, 5)1 -152.4595 5.2148 -29.236 < 0.0000000000000002 ***
## poly(lstat, 5)2 64.2272 5.2148 12.316 < 0.0000000000000002 ***
## poly(lstat, 5)3 -27.0511 5.2148 -5.187 0.00000031 ***
## poly(lstat, 5)4 25.4517 5.2148 4.881 0.00000142 ***
## poly(lstat, 5)5 -19.2524 5.2148 -3.692 0.000247 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.215 on 500 degrees of freedom
## Multiple R-squared: 0.6817, Adjusted R-squared: 0.6785
## F-statistic: 214.2 on 5 and 500 DF, p-value: < 0.00000000000000022Finally, we can also apply other transformations, e.g. taking the log of rm (average number of rooms per dwelling).
summary(lm(medv~I(log(rm)), data=Boston))##
## Call:
## lm(formula = medv ~ I(log(rm)), data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.487 -2.875 -0.104 2.837 39.816
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -76.488 5.028 -15.21 <0.0000000000000002 ***
## I(log(rm)) 54.055 2.739 19.73 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.915 on 504 degrees of freedom
## Multiple R-squared: 0.4358, Adjusted R-squared: 0.4347
## F-statistic: 389.3 on 1 and 504 DF, p-value: < 0.00000000000000022\(~\)
3.3 Variable Selection for Boston data
null.boston<-lm(medv~ 1, data=Boston) # the intercept only model
summary(null.boston)##
## Call:
## lm(formula = medv ~ 1, data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.533 -5.508 -1.333 2.467 27.467
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.5328 0.4089 55.11 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 9.197 on 505 degrees of freedomfull.boston<-lm(medv~ ., data=Boston) # include all predictors
summary(full.boston)##
## Call:
## lm(formula = medv ~ ., data = Boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.595 -2.730 -0.518 1.777 26.199
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 36.4594884 5.1034588 7.144 0.000000000003283 ***
## crim -0.1080114 0.0328650 -3.287 0.001087 **
## zn 0.0464205 0.0137275 3.382 0.000778 ***
## indus 0.0205586 0.0614957 0.334 0.738288
## chas 2.6867338 0.8615798 3.118 0.001925 **
## nox -17.7666112 3.8197437 -4.651 0.000004245643808 ***
## rm 3.8098652 0.4179253 9.116 < 0.0000000000000002 ***
## age 0.0006922 0.0132098 0.052 0.958229
## dis -1.4755668 0.1994547 -7.398 0.000000000000601 ***
## rad 0.3060495 0.0663464 4.613 0.000005070529023 ***
## tax -0.0123346 0.0037605 -3.280 0.001112 **
## ptratio -0.9527472 0.1308268 -7.283 0.000000000001309 ***
## black 0.0093117 0.0026860 3.467 0.000573 ***
## lstat -0.5247584 0.0507153 -10.347 < 0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.745 on 492 degrees of freedom
## Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
## F-statistic: 108.1 on 13 and 492 DF, p-value: < 0.00000000000000022## Compress the R output
### Forward selection
step(null.boston, scope=list(lower=null.boston, upper=full.boston), direction="forward", trace=0)##
## Call:
## lm(formula = medv ~ lstat + rm + ptratio + dis + nox + chas +
## black + zn + crim + rad + tax, data = Boston)
##
## Coefficients:
## (Intercept) lstat rm ptratio dis nox
## 36.341145 -0.522553 3.801579 -0.946525 -1.492711 -17.376023
## chas black zn crim rad tax
## 2.718716 0.009291 0.045845 -0.108413 0.299608 -0.011778### Backward (elimination) selection
step(full.boston, direction="backward", trace=0)##
## Call:
## lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad +
## tax + ptratio + black + lstat, data = Boston)
##
## Coefficients:
## (Intercept) crim zn chas nox rm
## 36.341145 -0.108413 0.045845 2.718716 -17.376023 3.801579
## dis rad tax ptratio black lstat
## -1.492711 0.299608 -0.011778 -0.946525 0.009291 -0.522553### Stepwise selection
step(null.boston, scope = list(upper=full.boston), direction="both", trace=0)##
## Call:
## lm(formula = medv ~ lstat + rm + ptratio + dis + nox + chas +
## black + zn + crim + rad + tax, data = Boston)
##
## Coefficients:
## (Intercept) lstat rm ptratio dis nox
## 36.341145 -0.522553 3.801579 -0.946525 -1.492711 -17.376023
## chas black zn crim rad tax
## 2.718716 0.009291 0.045845 -0.108413 0.299608 -0.011778\(~\)