Workshop 2
In this session we perform simple simulation exercises in order to investigate the properties of the sample mean introduced in the lectures. In this workshop we will use the loops and write our own functions in R.
To start, create a new R script by clicking on the corresponding menu button (in the top left); and save it somewhere in your computer. You can now write all your code into this file, and then execute it in R using the menu button Run or by simple pressing ctrl \(+\) enter.
1 Sampling without replacement
We’ll be using the hospital data set from the durham library in our sampling experiments. So, before we begin you’ll need to load the data:
- Refer to the worksheet from last time and either:
- Load the
durhamlibrary and thehospitaldata set. - If you have problems loading the library, use the code on this page to create the data set without the library
- Load the
- Create a new vector called
disch(or similar) containing the data for the number of discharges in thehospitaldata.
# solution
library(durham)
data(hospital)
disch <- hospital$dischargesRecall that our general approach to sampling is to sample without replacement, so we don’t repeatedly observe the same individual from the population. We can use R’s sample function to take random samples from a specified population vector, and we can do so either with or without replacement.
The sample function allows us to take a sample of a specified size from a vector of values which is treated as the population.
If we have a population vector pop and we want to take a sample of size n without replacement, then we use the following command:
sample(pop, n)
If we want to sample with replacement, then we can add the additional optional argument replace=TRUE.
Finally, the default is for all of the elements of the population to have equal probability. This can be changed to specified probability weights using the prob argument, but we won’t be looking into that any further. See the help file (by running ?sample) for more details on the sample function.
- Draw a sample (without replacement) of size \(n=4\) from the discharges data.
- Draw another sample of size \(n=4\), do you get the same sample values?
- Let us experiment with changing the sample size. For sample sizes \(n_1=4\), \(n_2=16\), and \(n_3=64\) generate a random sample, and compute its sample
mean. Do this in three lines, one for each sample size. - Compare the three means - what would you expect to see?
Click for solution
# (a)
sample(disch, 4)## [1] 2190 87 1153 1766# (b)
sample(disch, 4) ## unsurprisingly different## [1] 1009 1369 410 1093# (c)
mean(sample(disch,4))## [1] 287.75mean(sample(disch,16))## [1] 939.375mean(sample(disch,64))## [1] 859.2969# (d)
# potentially quite different values.
# We would expect the mean of these means to be mu,
# so the values should be centred about mu but its
# difficult to say more with only a few points\(~\)
We will be performing a repeated sampling experiment where we repeat the sampling many times to generate different samples each time. Then we can use the many samples to produce many different sample means, which we can explore to check their behaviour against what we would expect from the theory seen in lectures.
2 Functions and loops
To simplify the repeated sampling calculation, we will use a loop to repeat the calculations and we will write our own function to take care of the calculations we wish to perform during each iteration.
2.1 Functions
As with other programming languages (such as Python), we can combine multiple commands in R into our own custom functions that perform more complicated tasks or calculations. Throughout this course, we will be writing our own functions to solve specific problems and today we will learn the basic syntax of how to create a function.
When creating a new function, it needs to have a name, probably at least one argument (although it doesn’t have to), and a body of code that does something. At the end it usually should (although doesn’t have to) return a value or object out of the function.
The general syntax for writing your own function is
name.of.function <- function(arg1, arg2, arg3=2) {
# function code to do some useful stuff
return(something) # return value
}name.of.function: is the function’s name. This can be any valid variable name, but you should avoid using names that are used elsewhere in R, such asmean,function,plot, etc.arg1,arg2,arg3: these are the arguments of the function. You can write a function with any number of arguments, or none at all. These can be any R object: numbers, strings, arrays, data frames, or even other functions. Essentially, this is the list of everything that is needed for thename.of.functionfunction to run. Some arguments have default values specified, such asarg3in our example, which is set to2unless otherwise specified. Arguments without a default must have a value supplied for the function to run. You do not need to provide a value for those arguments with a default as they are considered as optional, and when omitted the function will simply use the default value in its definition.- Function body: The function code between the within the
{}brackets is run every time the function is called. Note that unlike Python where the code inside the function is indented, withRthe code inside the function must be enclosed in curly braces{}. This code might be very long or very short. Ideally functions are short and do just one thing – problems are rarely too small to benefit from some abstraction. Sometimes a large function is unavoidable, but usually these can be in turn constructed from a number of small functions. - Return value: The last line of the code is the value that will be returned by the function. It is not necessary that a function return anything, for example a function that makes a plot might not return anything (and so either state
return()or omitting thereturnstatement entirely), whereas a function that does a mathematical operation might return a number, or a vector.
For example, we can write a function to compute the sum of squares of two numbers as
sum.of.squares <- function(x,y) {
return(x^2 + y^2)
}and we can then evaluate
sum.of.squares(3,4)## [1] 25- Create a function called
MyFunthat takes a single argumentxand returns the value of \(1+x+0.1x^2\). - Use your function to evaluate \(1+x+0.1x^2\) when \(x=0\).
- Create a vector of the integers from \(0\) to \(100\), and evaluate \(1+x+0.1x^2\) for \(x=0,\dots,100\). You should do this in one line without resorting to any loops or iterative methods, or temporary variables. Hint: See the previous workshop for how to create vectors of integer sequences, and how to do arithmetic with vectors.
- Create another function called
MyFunPlotter, which takes a single argumentx, and which draws a scatterplotof the points(x, MyFun(x)). Evalate your function for \(x=0,\dots,100\). Hint: See the previous workshop for how to draw scatterplots, and use your function from the previous part of the question.
Click for solution
# (a)
MyFun <- function(x){
return(1+x+0.1*x^2)
}
# (b)
MyFun(0)## [1] 1# (c)
MyFun(0:100)## [1] 1.0 2.1 3.4 4.9 6.6 8.5 10.6 12.9 15.4 18.1
## [11] 21.0 24.1 27.4 30.9 34.6 38.5 42.6 46.9 51.4 56.1
## [21] 61.0 66.1 71.4 76.9 82.6 88.5 94.6 100.9 107.4 114.1
## [31] 121.0 128.1 135.4 142.9 150.6 158.5 166.6 174.9 183.4 192.1
## [41] 201.0 210.1 219.4 228.9 238.6 248.5 258.6 268.9 279.4 290.1
## [51] 301.0 312.1 323.4 334.9 346.6 358.5 370.6 382.9 395.4 408.1
## [61] 421.0 434.1 447.4 460.9 474.6 488.5 502.6 516.9 531.4 546.1
## [71] 561.0 576.1 591.4 606.9 622.6 638.5 654.6 670.9 687.4 704.1
## [81] 721.0 738.1 755.4 772.9 790.6 808.5 826.6 844.9 863.4 882.1
## [91] 901.0 920.1 939.4 958.9 978.6 998.5 1018.6 1038.9 1059.4 1080.1
## [101] 1101.0# (d)
MyFunPlotter <- function(x){
plot(x=x,y=MyFun(x))
}
MyFunPlotter(0:100)
\(~\)
2.2 Simple Loops
A “loop”” is a way to repeat a sequence of instructions under certain conditions. They allow you to automate parts of your code that are in need of repetition. We will look at two ways of creating loops in our code:
- Traditional loops which execute for a prescribed number of times, as controlled by a counter or an index, incremented at each iteration cycle are represented as
forloops in R. - Loops that take a function and apply that function to every element of a vector (or other array) are represented by the various
applyfunctions in R.
In R a for loop takes the following general form:
for (variable in sequence) {
## code to repeat goes here
}where variable is a name given to the iteration variable and which takes each possible value in the vector sequence at each pass through the loop.
Here is a quick trivial example, printing the square root of the integers one to ten:
for (x in 1:10) {
print(sqrt(x))
}- Sometimes big loops aren’t necessary! Write a single line of code that computes the square root of the integers \(1\) to \(10\) without using
for. - Use a
forloop to:- Print the values of the integers \(1\) to \(5\).
- Print the squares of the integers from \(10\) to \(3\).
- Print your first name 10 times.
Click for solution
# (a)
sqrt(1:10) ## use a vector instead## [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751 2.828427
## [9] 3.000000 3.162278# (b)
for(i in 1:5){
print(i)
}## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5for(i in 10:3){
print(i^2)
}## [1] 100
## [1] 81
## [1] 64
## [1] 49
## [1] 36
## [1] 25
## [1] 16
## [1] 9for(i in 1:10){
print("My Name")
}## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"
## [1] "My Name"\(~\)
While for loops are helpful when we need to explictly repeat a block of code, sometimes we just want to apply the same function (or calculations) to all of the elements of a vector. We can use for to do this, but R provides a function which does exactly that - sapply.
sapply applies a specified function to every element of a vector and returns a vector formed from the results.
sapply(X, FUN)
applies the function FUN to every element of the vector X it then returns a vector containing the values of FUN(X[1]), FUN(X[2]), and so on. So, to replicate the square-root example above using sapply, we would write
sapply(1:10, FUN=sqrt)
or alternatively
sapply(1:10, FUN=function(i){sqrt(i)})
which applies the square root function to each of the integers 1 to 10. Unlike a loop, sapply automatically returns its results as a vector without us having to write code for that (our for loop above only printed the values).
There are other variations of apply which work with matrices and other data structures, and we will see those later.
If we combine this technique of looping with the ability to write our own functions, then we have a very flexible way of re-writing a standard loop in a vectorised way. In general, using the sapply function is to be preferred to a for loop particularly when we want to keep the results of the calculations from each iteration. However, for loops are still useful and more natural in certain cases (where we do not want the output values, or where each iteration has a dependency on the calculations at the previous step).
- Use
sapplyto re-write your for-loops. You should write your answers in one line of code for each part:- Return the values of the integers \(1\) to \(5\).
- Return the squares of the integers from \(10\) to \(3\).
- Return a vector of your first name 10 times.
Click for solution
sapply(1:5, FUN=function(i) { i })## [1] 1 2 3 4 5sapply(10:3, FUN=function(i) { i^2 })## [1] 100 81 64 49 36 25 16 9sapply(1:10, FUN=function(i) { 'My Name' })## [1] "My Name" "My Name" "My Name" "My Name" "My Name" "My Name" "My Name"
## [8] "My Name" "My Name" "My Name"\(~\)
3 The Sampling Experiment
- Make a vector of the means of 30 different samples of size 4 from the hospital discharges vector using a combination of
sapplyand the functionssampleandmean. - Create a new function with argument
nthat returns a vector of the means of 1000 samples, each of sizen, from the discharges data. Hint: This is a one line function that places a version of the command used in the previous question within the function. - Using your new function, create three vectors containing the means for 1000 samples of sizes \(n_1=4\), \(n_2=16\) and \(n_3=64\) from the discharges data (giving each a name).
Click for solution
sapply(1:30, FUN=function(i) { mean(sample(disch, 4)) } )## [1] 541.50 987.50 729.75 1188.50 860.75 583.50 1613.00 1074.00 814.50
## [10] 860.25 1078.00 1176.00 1031.25 816.00 623.00 339.25 1231.00 967.00
## [19] 795.00 1282.50 777.75 820.50 580.50 545.00 770.75 641.75 857.50
## [28] 892.75 951.50 672.75dischSample <- function(n){
return(sapply(1:1000, FUN=function(i) { mean(sample(disch, n)) } ))
}
means4 <- dischSample(4)
means16 <- dischSample(16)
means64 <- dischSample(64)We now have samples of size 1000 from each of three sampling distributions of \(\bar{X}\), for when \(n=4\), \(n=16\), \(n=64\). As our samples of \(\bar{X}\) values are quite large in size, we might expect that each of these distributions is quite similar to the distribution of the underlying theoretical population of sample means.
- Find the mean and standard deviation for each collection of sample means. Do the results agree with what you would expect?
- Draw a
boxplotcomparing each of the three samples on the same scale. (Hint: see the previous workshop for how to draw a boxplot.)
Click for solution
mean(means4)## [1] 808.1368sd(means4)## [1] 293.6133mean(means16)## [1] 816.885sd(means16)## [1] 139.8785mean(means64)## [1] 818.0686sd(means64)## [1] 64.11728boxplot(means4, means16, means64, names = c("means4", "means16", "means64"))
\(~\)
R makes it easy to combine multiple plots into one overall graph, using either the par or layout functions.
With the par function, we specify the argument mfrow=c(nr, nc) to split the plot window into a grid of nr x nc plots that are filled in by row. For example, to divide the plot window into a 2x2 grid we call
par(mfrow=c(2,2))
This has no immediate effect, but the next four plots drawn (using plot, hist, boxplot, etc) will be drawn in the 2x2 grid.
To revert to a single plot layout, we ask for a 1x1 grid via par(mfrow=c(1,1)).
- Use the
parfunction with themfrowargument to configure to plot window for a column of three vertical plots. Note: this function will have no effect until you start drawing new plots. - Plot the samples of \(\bar{X}\) as separate histograms, one on top of the other. Make sure the horizontal axes are the same (Hint: use the
xlimargument to specify the horizontal axis limits, andrangewill determine the min and max of a vector).
Click for solution
par(mfrow=c(3,1))
hist(means4, xlim=range(means4))
hist(means16, xlim=range(means4))
hist(means64, xlim=range(means4))
It is often useful to add simple straight lines to lines to plots, which can be achieved using the abline function. abline can be used in three different ways:
- Draw a horizontal line: pass a value to the
hargument,abline(h=3)draws a horizontal line at \(y=3\) - Draw a vertical line: pass a value to the
vargument,abline(v=5)draws a vertical line at \(x=5\) - Draw a line with given intercept and slope: pass value to the
aandbarguments representing the intercept and slope respectively;abline(a=1,b=2)draws the line at \(y=1+2x\)
abline can be customised using any of the usual colour and line modifications using colour (col), line types and widths (lty, and lwd).
- Redraw your histograms, this time adding a vertical line showing the population mean.
Click for solution
par(mfrow=c(3,1))
hist(means4, xlim=range(means4))
abline(v=mean(disch),col='red')
hist(means16, xlim=range(means4))
abline(v=mean(disch),col='red')
hist(means64, xlim=range(means4))
abline(v=mean(disch),col='red')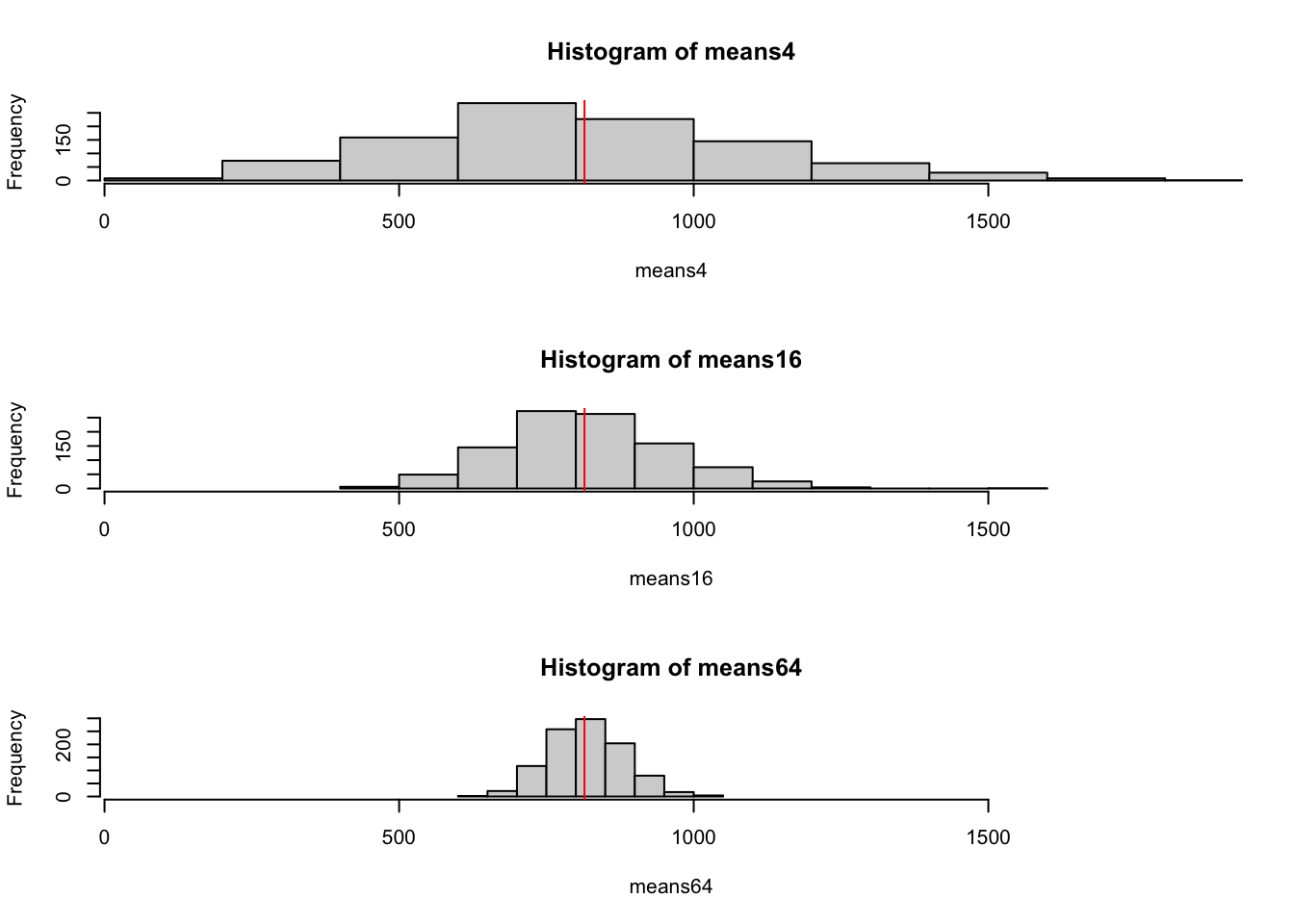
\(~\) According to theory seen in lectures, the sample mean is an unbiased estimator of the population mean, \(\mu\), and has variance denoted \(\sigma^2_{\bar{X}}\). For Normal data or large sample sizes, the sampling distribution is either exactly or approximately Normal with the above mean and variance.
- What do you observe about the three distributions? Does the picture correspond to the theory?
- What do you notice about the mean and standard deviation of your samples relative to the population for the three different sample sizes.
Click for solution
## distributions are all centred about mu (as they should be since Xbar is unbiased)
## spread decreases with sample size (due primarily to the 1/n term in the variance of Xbar)
## the distribution looks "more Normal" as n gets bigger (central limit theorem)\(~\)
If you finish, you can investigate some of the additional problems below.
4 The variance of the sample mean
We can use R to investigate the properties of the distribution of the sample mean more closely. The theory tells us that the variance of the sample mean, \(\bar{X}\), for a sample of size \(n\) from a finite population of size \(N\) is given by:
\[ \text{Var}[\bar{X}] = \sigma^2_{\bar{X}} = \left(\frac{N-n}{N-1}\right)\frac{\sigma^2}{n}, \sigma^2 = \frac{1}{N} \sum_{i=1}^{N}(X_i-E(X_i))^2 \] where \(\sigma^2\) is the population variance of the original data, \(X_i\). An unbiased estimator of this variance is the estimated variance, given by \[ S^2_{\bar{X}} = \left(1-\frac{n}{N}\right)\frac{s^2}{n}, \] where \(s^2\) is the sample variance.
- Calculate the true variance of the sample mean, \(\sigma^2_{\bar{X}}\) for the samples of size 4, 16 and 64.
- Write a new function with argument
nthat returns a vector of 1000 realisations of \(S^2_{\bar{X}}\) for samples ofnfrom the discharges data. - Evaluate your function for \(n=4\), \(n=16\), and \(n=64\) and store the result to three variables.
- Display each of these three samples as histograms, one on top of the other in the same plot. Make sure the horizontal axes are the same.
- Draw a vertical line on each one showing the location of the true variance of the sample mean in each case.
- Is the result of this experiment consistent with the theory? Why?
Click for solution
## Careful with this step, as using `var` on the discharges vector uses the sample variance formula which
## assumes the sample mean is not mu and which divides by (c-1). We need the population variance as
## mean(disch)=mu since this is our population, and we want to divide by N. So either we need to correct the
## output from var or compute directly.
# (a)
N <- length(disch)
sigma2 <- sum((disch-mean(disch))^2)/N
## or
sigma2 <- (N-1)/N * var(disch)
## compute sigma_xbar for n=4,16,64 - we should probably do this with a function!
trueV4 <- (N-4)/(N-1) * sigma2/4
trueV16 <- (N-16)/(N-1) * sigma2/16
trueV64 <- (N-64)/(N-1) * sigma2/64
# (b)
## easiest to do this with a new function to compute S^2_Xbar for a given sample
S2Xbar <- function(x){
n <- length(x)
return( (1-n/N)*var(x)/n)
}
## then just swap `mean` for `S2Xbar` from our previous sampling function
dischVariances <- function(n){
return(sapply(1:1000, FUN=function(i) { S2Xbar(sample(disch, n)) } ))
}
# (c)
vars4 <- dischVariances(4)
vars16 <- dischVariances(16)
vars64 <- dischVariances(64)
# (d), (e), and (f)
par(mfrow=c(3,1))
hist(vars4, xlim=range(vars4))
abline(v=trueV4,col='red')
hist(vars16, xlim=range(vars4))
abline(v=trueV16,col='red')
hist(vars64, xlim=range(vars4))
abline(v=trueV64,col='red')