Labs on Variable Selection and Resampling Methods

This worksheet covers variable selection and resampling methods in the context of linear regression; the idea is for you to work through it over the course of the three computer labs in the third week of the module. You will receive direction as to which sections to focus on in each lab depending on our progress through the material in the lecture-workshops. The worksheet is designed to give you some experience working with best subset selection in R and in writing your own R code to perform cross-validation. Some of the R functions that we write and use in the main text are beyond what I would expect you to be able to write from scratch at this stage in your studies. However, try to understand how they work; if you have any questions, please just ask in the lab or send me an email.

1 Background

The data we will use in this series of labs were collected in a study concerning patients with diabetes. The response variable of interest was disease progression one year after taking baseline measurements on various clinical variables. For each of \(n=442\) patients, the data comprise a quantitative measure of disease progression (dis) and measurements on \(p=10\) baseline (predictor) variables: age (age), sex (sex), body mass index (bmi), average blood pressure (map) and six blood serum measurements (tc, ldl, hdl, tch, ltg, glu). We will use multiple linear regression to develop a model for predicting disease progression on the basis of one or more of the baseline variables.

The data can be found in the diabetes data set which is part of the durhamSLR package. Like the ElemStatLearn package from the Lecture-Workshops, the package must be installed from source. After downloading the file durhamSLR_0.2.0.tar.gz from Ultra, save it in a directory of your choice. The package can then be installed in RStudio by going to Tools then Install Packages. In the pop-up box that appears, change the drop-down option for “Install from:” to “Package Archive File (.tar.gz)”. Then navigate to the file durhamSLR_0.2.0.tar.gz and click Open. Finally click Install. Note that you may get an error referring to the plyr package. If so, you need to install the package plyr before installing the durhamSLR package. You can install plyr directly from CRAN via:

install.packages("plyr")

Once it is installed, the durhamSLR package and data can then be loaded into R and inspected in the usual way:

## Load the  durhamSLR package
library( durhamSLR)
## Load the data
data(diabetes)
## Check size
dim(diabetes)

## [1] 442  11

## Store n and p:
(n = nrow(diabetes))

## [1] 442

(p = ncol(diabetes) - 1)

## [1] 10

## Print first few rows
head(diabetes)

##            age         sex         bmi          map           tc         ldl          hdl          tch          ltg
## 1  0.038075906  0.05068012  0.06169621  0.021872355 -0.044223498 -0.03482076 -0.043400846 -0.002592262  0.019908421
## 2 -0.001882017 -0.04464164 -0.05147406 -0.026327835 -0.008448724 -0.01916334  0.074411564 -0.039493383 -0.068329744
## 3  0.085298906  0.05068012  0.04445121 -0.005670611 -0.045599451 -0.03419447 -0.032355932 -0.002592262  0.002863771
## 4 -0.089062939 -0.04464164 -0.01159501 -0.036656447  0.012190569  0.02499059 -0.036037570  0.034308859  0.022692023
## 5  0.005383060 -0.04464164 -0.03638469  0.021872355  0.003934852  0.01559614  0.008142084 -0.002592262 -0.031991445
## 6 -0.092695478 -0.04464164 -0.04069594 -0.019442093 -0.068990650 -0.07928784  0.041276824 -0.076394504 -0.041180385
##            glu dis
## 1 -0.017646125 151
## 2 -0.092204050  75
## 3 -0.025930339 141
## 4 -0.009361911 206
## 5 -0.046640874 135
## 6 -0.096346157  97

We see that the response variable (dis) is stored in column 11 and that the predictor variables appear in columns 1–10. It appears that the predictor variables are not in their “raw” form, i.e. they seem to have been transformed. To investigate we can check the means and standard deviations of the predictor variables:

colMeans(diabetes[,1:10])

##                        age                        sex                        bmi                        map 
## -0.00000000000000036531922  0.00000000000000012880911 -0.00000000000000080087230  0.00000000000000012899111 
##                         tc                        ldl                        hdl                        tch 
## -0.00000000000000009112498  0.00000000000000013015258 -0.00000000000000045576818  0.00000000000000038659215 
##                        ltg                        glu 
## -0.00000000000000038614792 -0.00000000000000034022264

## These numbers are tiny; this is easier to see if we round them:
round(colMeans(diabetes[,1:10]), 4)

## age sex bmi map  tc ldl hdl tch ltg glu 
##   0   0   0   0   0   0   0   0   0   0

apply(diabetes[,1:10], 2, sd)

##        age        sex        bmi        map         tc        ldl        hdl        tch        ltg        glu 
## 0.04761905 0.04761905 0.04761905 0.04761905 0.04761905 0.04761905 0.04761905 0.04761905 0.04761905 0.04761905

Although the predictor variables have been transformed to have mean zero, the standard deviations are not equal to one. It turns out that, instead, each variable has been transformed so that the sum of the squared values is equal to one.

• Write some R code to verify that the sum of the squared values in each of the first ten columns of the prostate data frame is equal to one.
• Please have a go by yourself before uncovering the solution.

Click for solution

## Function to compute the sum of squares
sumofsquares = function(x) sum(x^2)
## Loop over columns
ss = numeric(10)
for(i in 1:10) {
  ss[i] = sumofsquares(diabetes[,i])
}
ss

##  [1] 1 1 1 1 1 1 1 1 1 1

## This can be done more efficiently by using the apply function:
apply(diabetes[,1:10], 2, sumofsquares)

## age sex bmi map  tc ldl hdl tch ltg glu 
##   1   1   1   1   1   1   1   1   1   1

2 Exploratory Data Analysis

Before proceeding with our regression analysis, we will perform some exploratory analysis to get a feel for the relationships between the response and predictor variables, and the relationships amongst the predictor variables. We can produce a scatterplot matrix as follows:

pairs(diabetes)

Figure 2.1: Scatterplot matrix for the diabetes data.

A few of the variables seem to show a weak linear relationship with the response, most notably bmi and ltg. For other variables, such as age and sex, there is little evidence of a linear relationship with the response. However, it is also clear that a few of the predictor variables are themselves highly correlated, for example, the blood serum measurements tc and ldl. This immediately suggests that we may be able to omit some predictor variables when we fit our multiple linear regression model.

• By applying the cor function to the diabetes data set, compute the sample correlation matrix and confirm that the observations above are borne out through the sample correlations.
• Please have a go by yourself before uncovering the solution.

Click for solution

## Apply the correlation function
cor(diabetes)

##             age         sex        bmi        map         tc        ldl         hdl        tch        ltg
## age  1.00000000  0.17373710  0.1850847  0.3354267 0.26006082  0.2192431 -0.07518097  0.2038409  0.2707768
## sex  0.17373710  1.00000000  0.0881614  0.2410132 0.03527682  0.1426373 -0.37908963  0.3321151  0.1499176
## bmi  0.18508467  0.08816140  1.0000000  0.3954153 0.24977742  0.2611699 -0.36681098  0.4138066  0.4461586
## map  0.33542671  0.24101317  0.3954153  1.0000000 0.24246971  0.1855578 -0.17876121  0.2576534  0.3934781
## tc   0.26006082  0.03527682  0.2497774  0.2424697 1.00000000  0.8966630  0.05151936  0.5422073  0.5155008
## ldl  0.21924314  0.14263726  0.2611699  0.1855578 0.89666296  1.0000000 -0.19645512  0.6598169  0.3183534
## hdl -0.07518097 -0.37908963 -0.3668110 -0.1787612 0.05151936 -0.1964551  1.00000000 -0.7384927 -0.3985770
## tch  0.20384090  0.33211509  0.4138066  0.2576534 0.54220728  0.6598169 -0.73849273  1.0000000  0.6178574
## ltg  0.27077678  0.14991756  0.4461586  0.3934781 0.51550076  0.3183534 -0.39857700  0.6178574  1.0000000
## glu  0.30173101  0.20813322  0.3886800  0.3904294 0.32571675  0.2906004 -0.27369730  0.4172121  0.4646705
## dis  0.18788875  0.04306200  0.5864501  0.4414838 0.21202248  0.1740536 -0.39478925  0.4304529  0.5658834
##            glu        dis
## age  0.3017310  0.1878888
## sex  0.2081332  0.0430620
## bmi  0.3886800  0.5864501
## map  0.3904294  0.4414838
## tc   0.3257168  0.2120225
## ldl  0.2906004  0.1740536
## hdl -0.2736973 -0.3947893
## tch  0.4172121  0.4304529
## ltg  0.4646705  0.5658834
## glu  1.0000000  0.3824835
## dis  0.3824835  1.0000000

We see that the predictor variables that have the strongest linear association with the response (dis) are bmi, with a correlation of 0.5864501, and ltg, with a correlation of 0.5658834. These suggest moderate positive linear relationships. The predictor variables that have the weakest linear association with the response (dis) are sex, with a correlation of 0.043062, ldl, with a correlation of 0.1740536 and age, with a correlation of 0.1878888. These all suggest very weak positive linear relationships. The pair of predictor variables with the strongest linear association is ldl and tc which have a correlation of 0.896663 indicating a strong, positive linear relationship.

3 Multiple Linear Regression

3.1 The Full Model

Let \(Y\) denote disease progression and denote by \(x_{j}\) the (standardised) measurement on the \(j\)-th baseline variable. Consider the multiple linear regression model: \[\begin{equation*} Y = \beta_0 + \beta_1 x_1 + \ldots + \beta_p x_p + \epsilon. \end{equation*}\] We will begin by fitting the full model via least squares using the lm function:

## Fit model using least squares
lsq_fit = lm(dis ~ ., data=diabetes)

We can then obtain a summary of the fitted model by passing the returned object to the summary function:

## Summarise fitted model
(lsq_summary = summary(lsq_fit))

## 
## Call:
## lm(formula = dis ~ ., data = diabetes)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -155.829  -38.534   -0.227   37.806  151.355 
## 
## Coefficients:
##             Estimate Std. Error t value             Pr(>|t|)    
## (Intercept)  152.133      2.576  59.061 < 0.0000000000000002 ***
## age          -10.012     59.749  -0.168             0.867000    
## sex         -239.819     61.222  -3.917             0.000104 ***
## bmi          519.840     66.534   7.813    0.000000000000043 ***
## map          324.390     65.422   4.958    0.000001023818915 ***
## tc          -792.184    416.684  -1.901             0.057947 .  
## ldl          476.746    339.035   1.406             0.160389    
## hdl          101.045    212.533   0.475             0.634721    
## tch          177.064    161.476   1.097             0.273456    
## ltg          751.279    171.902   4.370    0.000015560214564 ***
## glu           67.625     65.984   1.025             0.305998    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 54.15 on 431 degrees of freedom
## Multiple R-squared:  0.5177, Adjusted R-squared:  0.5066 
## F-statistic: 46.27 on 10 and 431 DF,  p-value: < 0.00000000000000022

The column of \(p\)-values (i.e. the Pr(>|t|) column) for the \(t\)-tests \[\begin{equation*} H_0: \beta_j = 0 \quad \text{versus} \quad H_1: \beta_j \ne 0 \end{equation*}\] confirms our observations from the exploratory analysis; if we consider the predictor variables one-at-a-time, there are several which would not be needed in a model containing all others. We also see that the coefficient of determination, \(R^2\), is equal to 51.77%.

• How would you interpret this value for \(R^2\).
• Please think about this yourself before uncovering the solution.

Click for solution

The value of \(R^2\) means that 51.77% of the variation in the quantitative measure of disease progression (dis) can be explained by its linear regression on the 10 baseline (predictor) variables.

We can use R to calculate the values \(\hat{y}_1,\ldots,\hat{y}_n\) that our fitted model would predict for the predictor variables on the 1st, \(\ldots\), \(n\)th rows of our matrix of predictor variables by using the predict function. As arguments to the predict function, we simply pass the object returned by the lm function and the data frame containing the predictor variables at which we want predictions. In this case we have:

## Compute the fitted values: 
yhat = predict(lsq_fit, diabetes)
## Print first few elements:
head(yhat)

##         1         2         3         4         5         6 
## 206.11707  68.07235 176.88406 166.91797 128.45984 106.34909

## Compare with actual values:
head(diabetes$dis)

## [1] 151  75 141 206 135  97

• Referring back to your notes from the lecture-workshop if necessary, calculate the training error for this model.
• Please think about this yourself before uncovering the solution.

Click for solution

## Compute the fitted values: did this above and they are stored in yhat
## Compute training error:
(training_error = mean((diabetes$dis - yhat)^2))

## [1] 2859.69

3.2 \(k\)-fold Cross-Validation

To get an assessment of the predictive performance of the full model, we will write some code to estimate the test error. Given a particular split of the data into a training set and a validation set, the following general function estimates the test mean-squared error (MSE):

reg_fold_error = function(X, y, test_data) {
  Xy = data.frame(X, y=y)
  ## Fit the model to the training data
  if(ncol(Xy)>1) tmp_fit = lm(y ~ ., data=Xy[!test_data,])
  else tmp_fit = lm(y ~ 1, data=Xy[!test_data,,drop=FALSE])
  ## Generate predictions over the test data
  yhat = predict(tmp_fit, Xy[test_data,,drop=FALSE])
  yobs = y[test_data]
  ## Compute the test MSE
  test_error = mean((yobs - yhat)^2)
  return(test_error)
}

The arguments of this function are:

• X: predictor variables in a \(n \times p\) matrix.
• y: response variable in a vector of length \(n\).
• test_data: a logical vector whose \(i\)th element is equal to TRUE if observation \(i\) is in the test set and equal to FALSE if observation \(i\) is in the training set.

Note that the argument drop=FALSE on lines 4 and 6 in the body of the function is simply there to allow it to work even when there are no predictor variables (i.e. when the dimension of X is \(n \times 0\)), which is called the null model. In this case Xy, created on line 1, would be \(n \times 1\) and the argument drop=FALSE prevents R from converting the two-dimensional object Xy into a 1-dimensional object (i.e. from “dropping” a dimension) when we pick out a subset of the rows. If we omitted the drop=FALSE arguments, the lm and predict functions would terminate with errors for this special case. The following code illustrates the basic idea:

df = data.frame(y=rnorm(3))
df

##           y
## 1 0.5452946
## 2 0.2174415
## 3 0.1551941

df[1:3,]

## [1] 0.5452946 0.2174415 0.1551941

df[1:3,,drop=FALSE]

##           y
## 1 0.5452946
## 2 0.2174415
## 3 0.1551941

In this lab, we will focus on estimating the test error using \(k\)-fold cross-validation. Recall that \(k\)-fold cross-validation works by randomly dividing the data into \(k\) folds of approximately equal size. The last \(k-1\) folds are used as the training data then the first fold is used as a test set. We compute the test error rate based on this first fold and call it \(MSE_1\). The process is then repeated using the second fold as the test set to get \(MSE_2\), then the third fold to get \(MSE_3\), and so on. Eventually this procedure gives us \(k\) estimates of the test MSE, \(MSE_1, \ldots, MSE_k\) which are averaged to give the overall test MSE.

Before we randomly divide our data into folds, we will set the seed of R’s random number generator so that repeating the analysis later will produce exactly the same results:

## Set the seed to make the analysis reproducible
set.seed(1)

Now, suppose we wish to carry out 10-fold cross-validation, i.e. \(k=10\). We therefore need to randomly divide the data into 10 folds of approximately equal size. We do this by sampling a fold from \(\{ 1, 2, \ldots, 10 \}\) where each fold has the same probability of being selected. We can do this for each observation \(i=1,\ldots,n\) as follows:

## 10-fold cross validation
k = 10
## Sample fold-assignment index
fold_index = sample(k, n, replace=TRUE)
## Print first few fold-assignments
head(fold_index)

## [1] 9 4 7 1 2 7

So observation 1 is assigned to fold 9, observation 2 is assigned to fold 4, and so on.

We already have a function that can calculate the test error for any particular fold, namely the function reg_fold_error. For example, to use it to calculate the test MSE for fold 1, we would just need to set its third argument (test_data) to be a vector of booleans, with a TRUE in position \(i\) if observation \(i\) is assigned to fold 1 and a FALSE in position \(i\) otherwise. We can construct such a vector using the == relational operator. This can be used to test whether each element in the vector on the left is equal to the number on the right:

c(3, 4, 2, 1, 4, 3, 3, 1) == 1

## [1] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE

## We can also assign the output to a variable so it can be stored:
demo = c(3, 4, 2, 1, 4, 3, 3, 1) == 1
demo

## [1] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE

We can apply these ideas to write a function that uses reg_fold_error to estimate the test MSE using \(k\)-fold cross validation:

regression_cv = function(X, y, fold_ind) {
  p = ncol(X)
  Xy = cbind(X, y=y)
  nfolds = max(fold_ind)
  if(!all.equal(sort(unique(fold_ind)), 1:nfolds)) stop("Invalid fold partition.")
  fold_errors = numeric(nfolds)
  # Compute the test MSE for each fold
  for(fold in 1:nfolds) {
    test_data = fold_ind==fold
    fold_errors[fold] = reg_fold_error(X, y, test_data)
  }
  # Find the fold sizes
  fold_sizes = numeric(nfolds)
  for(fold in 1:nfolds) fold_sizes[fold] = length(which(fold_ind==fold))
  # Compute the average test MSE across folds
  test_error = weighted.mean(fold_errors, w=fold_sizes)
  # Return the test error
  return(test_error)
}

We can now apply the function to calculate the test MSE for our full regression model for the diabetes data:

(test_MSE = regression_cv(diabetes[,1:p], diabetes[,p+1], fold_index))

## [1] 3061.009

• Look at the help file for the weighted.mean function by typing ?weighted.mean in the console.
• Why do we use the weighted.mean function (and not just the mean function) to average \(MSE_1, \ldots, MSE_k\) in the regression_cv function?
• Please think about this yourself before uncovering the solution.

Click for solution

The folds will not have exactly the same size as we can easily verify:

fold_sizes = numeric(k)
for(fold in 1:k) fold_sizes[fold] = length(which(fold_index==fold))
fold_sizes

##  [1] 45 36 47 44 52 42 42 40 47 47

To allow for this, the MSE estimates are weighted by the sizes of the folds.

Before moving on, it is convenient to note that the only line in regression_cv that depends on the supervised learning method (multiple linear regression in this case) is

    fold_errors[fold] = reg_fold_error(X, y, test_data)

because our reg_fold_error function was written to calculate the test error associated with a linear regression model. Now, suppose we wanted to use \(k\)-fold cross-validation to estimate the test error of a classification method, instead of linear regression. To do this, we could simply replace the call to the reg_fold_error function with a call to a function that performed an analogous calculation to compute the test error for that classification method. We can therefore make our function more general, and appropriate for re-use with classification methods, by replacing the line above with

    fold_errors[fold] = fold_error_function(X, y, test_data)

and then making fold_error_function an argument to the parent function. (This works because in R a function can be treated like any other object, e.g. we can pass a function as an argument to another function, write functions which return other functions, and so on). In other words, we write:

general_cv = function(X, y, fold_ind, fold_error_function) {
  p = ncol(X)
  Xy = cbind(X, y=y)
  nfolds = max(fold_ind)
  if(!all.equal(sort(unique(fold_ind)), 1:nfolds)) stop("Invalid fold partition.")
  fold_errors = numeric(nfolds)
  # Compute the test error for each fold
  for(fold in 1:nfolds) {
    test_data = fold_ind==fold
    fold_errors[fold] = fold_error_function(X, y, test_data)
  }
  # Find the fold sizes
  fold_sizes = numeric(nfolds)
  for(fold in 1:nfolds) fold_sizes[fold] = length(which(fold_ind==fold))
  # Compute the average test error across folds
  test_error = weighted.mean(fold_errors, w=fold_sizes)
  # Return the test error
  return(test_error)
}

And then apply it to linear regression by setting the fourth argument equal to reg_fold_error:

(test_MSE = general_cv(diabetes[,1:p], diabetes[,p+1], fold_index, reg_fold_error))

## [1] 3061.009

Of course, we get exactly the same estimate of the test MSE as before because the two function calls are equivalent. We will use our general_cv function again next week when we study classification methods.

3.3 Best Subset Selection

Both our exploratory data analysis and the hypothesis tests that individual coefficients are equal to zero suggest that we do not need to include all the predictor variables in our fitted model. If we can eliminate some of the predictor variables we might be able to estimate the effects of those that remain more precisely, thereby improving the predictive performance of the model. To this end, we will consider best subset selection.

3.3.1 Model fitting

We can perform best subset selection using the regsubsets function from the leaps R package. We begin by loading the package

library(leaps)

Next we use the regsubsets function to apply the algorithm, specifying method="exhaustive" to indicate that we want to perform best subset selection and nvmax=p to indicate that we want to consider models with \(1, 2, \ldots, p\) predictor variables. The function identifies the best model that contains each number of predictors. Denote these models by \(\mathcal{M}_1,\ldots,\mathcal{M}_p\). Again, we can summarise the results of the model fitting exercise using the summary function which prints the predictor variables in \(\mathcal{M}_1,\ldots,\mathcal{M}_p\).

## Apply the best subset selection algorithm
bss_fit = regsubsets(dis ~ ., data=diabetes, method="exhaustive", nvmax=p)
## Summarise the results
(bss_summary = summary(bss_fit))

## Subset selection object
## Call: regsubsets.formula(dis ~ ., data = diabetes, method = "exhaustive", 
##     nvmax = p)
## 10 Variables  (and intercept)
##     Forced in Forced out
## age     FALSE      FALSE
## sex     FALSE      FALSE
## bmi     FALSE      FALSE
## map     FALSE      FALSE
## tc      FALSE      FALSE
## ldl     FALSE      FALSE
## hdl     FALSE      FALSE
## tch     FALSE      FALSE
## ltg     FALSE      FALSE
## glu     FALSE      FALSE
## 1 subsets of each size up to 10
## Selection Algorithm: exhaustive
##           age sex bmi map tc  ldl hdl tch ltg glu
## 1  ( 1 )  " " " " "*" " " " " " " " " " " " " " "
## 2  ( 1 )  " " " " "*" " " " " " " " " " " "*" " "
## 3  ( 1 )  " " " " "*" "*" " " " " " " " " "*" " "
## 4  ( 1 )  " " " " "*" "*" "*" " " " " " " "*" " "
## 5  ( 1 )  " " "*" "*" "*" " " " " "*" " " "*" " "
## 6  ( 1 )  " " "*" "*" "*" "*" "*" " " " " "*" " "
## 7  ( 1 )  " " "*" "*" "*" "*" "*" " " "*" "*" " "
## 8  ( 1 )  " " "*" "*" "*" "*" "*" " " "*" "*" "*"
## 9  ( 1 )  " " "*" "*" "*" "*" "*" "*" "*" "*" "*"
## 10  ( 1 ) "*" "*" "*" "*" "*" "*" "*" "*" "*" "*"

The bss_summary object contains a lot of useful information. We can examine its structure by executing the R expression

str(bss_summary)

## List of 8
##  $ which : logi [1:10, 1:11] TRUE TRUE TRUE TRUE TRUE TRUE ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:10] "1" "2" "3" "4" ...
##   .. ..$ : chr [1:11] "(Intercept)" "age" "sex" "bmi" ...
##  $ rsq   : num [1:10] 0.344 0.459 0.48 0.492 0.509 ...
##  $ rss   : num [1:10] 1719582 1416694 1362708 1331430 1287879 ...
##  $ adjr2 : num [1:10] 0.342 0.457 0.477 0.487 0.503 ...
##  $ cp    : num [1:10] 148.35 47.07 30.66 22 9.15 ...
##  $ bic   : num [1:10] -174 -254 -265 -269 -278 ...
##  $ outmat: chr [1:10, 1:10] " " " " " " " " ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : chr [1:10] "1  ( 1 )" "2  ( 1 )" "3  ( 1 )" "4  ( 1 )" ...
##   .. ..$ : chr [1:10] "age" "sex" "bmi" "map" ...
##  $ obj   :List of 28
##   ..$ np       : int 11
##   ..$ nrbar    : int 55
##   ..$ d        : num [1:11] 442 1 0.455 0.823 0.379 ...
##   ..$ rbar     : num [1:55] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ thetab   : num [1:11] 152 697 -274 410 -253 ...
##   ..$ first    : int 2
##   ..$ last     : int 11
##   ..$ vorder   : int [1:11] 1 9 8 11 7 6 5 3 10 4 ...
##   ..$ tol      : num [1:11] 0.000000010512 0.000000001273 0.000000001064 0.000000001149 0.000000000917 ...
##   ..$ rss      : num [1:11] 2621009 2135363 2101268 1962593 1938429 ...
##   ..$ bound    : num [1:11] 2621009 1719582 1416694 1362708 1331430 ...
##   ..$ nvmax    : int 11
##   ..$ ress     : num [1:11, 1] 2621009 1719582 1416694 1362708 1331430 ...
##   ..$ ir       : int 11
##   ..$ nbest    : int 1
##   ..$ lopt     : int [1:66, 1] 1 1 4 1 4 10 1 4 5 10 ...
##   ..$ il       : int 66
##   ..$ ier      : int 0
##   ..$ xnames   : chr [1:11] "(Intercept)" "age" "sex" "bmi" ...
##   ..$ method   : chr "exhaustive"
##   ..$ force.in : Named logi [1:11] TRUE FALSE FALSE FALSE FALSE FALSE ...
##   .. ..- attr(*, "names")= chr [1:11] "" "age" "sex" "bmi" ...
##   ..$ force.out: Named logi [1:11] FALSE FALSE FALSE FALSE FALSE FALSE ...
##   .. ..- attr(*, "names")= chr [1:11] "" "age" "sex" "bmi" ...
##   ..$ sserr    : num 1263983
##   ..$ intercept: logi TRUE
##   ..$ lindep   : logi [1:11] FALSE FALSE FALSE FALSE FALSE FALSE ...
##   ..$ nullrss  : num 2621009
##   ..$ nn       : int 442
##   ..$ call     : language regsubsets.formula(dis ~ ., data = diabetes, method = "exhaustive", nvmax = p)
##   ..- attr(*, "class")= chr "regsubsets"
##  - attr(*, "class")= chr "summary.regsubsets"

One component which will be particularly helpful when we come to consider best-subset selection is the which component which indicates which predictors were used in the best-fitting model with \(1,\ldots,p\) predictors. It can be extracted using using the usual $ notation:

bss_summary$which

##    (Intercept)   age   sex  bmi   map    tc   ldl   hdl   tch   ltg   glu
## 1         TRUE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 2         TRUE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
## 3         TRUE FALSE FALSE TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE
## 4         TRUE FALSE FALSE TRUE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE
## 5         TRUE FALSE  TRUE TRUE  TRUE FALSE FALSE  TRUE FALSE  TRUE FALSE
## 6         TRUE FALSE  TRUE TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE FALSE
## 7         TRUE FALSE  TRUE TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE
## 8         TRUE FALSE  TRUE TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE
## 9         TRUE FALSE  TRUE TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## 10        TRUE  TRUE  TRUE TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

Let’s exclude the first column, all of whose entries must be TRUE since all models must have an intercept:

(predictor_indicator = bss_summary$which[,2:(p+1)])

##      age   sex  bmi   map    tc   ldl   hdl   tch   ltg   glu
## 1  FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## 2  FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE
## 3  FALSE FALSE TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE
## 4  FALSE FALSE TRUE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE
## 5  FALSE  TRUE TRUE  TRUE FALSE FALSE  TRUE FALSE  TRUE FALSE
## 6  FALSE  TRUE TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE FALSE
## 7  FALSE  TRUE TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE
## 8  FALSE  TRUE TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE
## 9  FALSE  TRUE TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## 10  TRUE  TRUE TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

As we can see, this is now a \(p \times p\) matrix of booleans whose \((i,j)\)th entry is TRUE if \(\mathcal{M}_i\) uses the \(j\)th predictor and FALSE otherwise. We can use this matrix to pick out only the columns of our matrix of predictors that correspond to \(\mathcal{M}_1,\ldots,\mathcal{M}_p\). To illustrate:

## Pick out the first few observations on the p predictor variables
(demo = diabetes[1:3, 1:p])

##            age         sex         bmi          map           tc         ldl         hdl          tch          ltg
## 1  0.038075906  0.05068012  0.06169621  0.021872355 -0.044223498 -0.03482076 -0.04340085 -0.002592262  0.019908421
## 2 -0.001882017 -0.04464164 -0.05147406 -0.026327835 -0.008448724 -0.01916334  0.07441156 -0.039493383 -0.068329744
## 3  0.085298906  0.05068012  0.04445121 -0.005670611 -0.045599451 -0.03419447 -0.03235593 -0.002592262  0.002863771
##           glu
## 1 -0.01764613
## 2 -0.09220405
## 3 -0.02593034

## Select only the predictor variables that appear in, say, M_2
demo[1:3, predictor_indicator[2,]]

##           bmi          ltg
## 1  0.06169621  0.019908421
## 2 -0.05147406 -0.068329744
## 3  0.04445121  0.002863771

## Select only the predictor variables that appear in, say, M_5
demo[1:3, predictor_indicator[5,]]

##           sex         bmi          map         hdl          ltg
## 1  0.05068012  0.06169621  0.021872355 -0.04340085  0.019908421
## 2 -0.04464164 -0.05147406 -0.026327835  0.07441156 -0.068329744
## 3  0.05068012  0.04445121 -0.005670611 -0.03235593  0.002863771

The other very useful components of the bss_summary object are the various model comparison criteria. To compare the fits of the models \(\mathcal{M}_1,\ldots,\mathcal{M}_p\), we can use adjusted-\(R^2\), Mallow’s \(C_p\) statistic or the BIC, which can be extracted as follows:

bss_summary$adjr2

##  [1] 0.3424327 0.4570228 0.4765217 0.4873665 0.5029975 0.5081936 0.5084895 0.5085563 0.5076705 0.5065603

bss_summary$cp

##  [1] 148.352561  47.072229  30.663634  21.998461   9.148045   5.560162   6.303221   7.248522   9.028080  11.000000

bss_summary$bic

##  [1] -174.1108 -253.6592 -264.7407 -268.9126 -277.5210 -277.0899 -272.2819 -267.2702 -261.4049 -255.3424

The best models, according to each criteria are therefore

(best_adjr2 = which.max(bss_summary$adjr2))

## [1] 8

(best_cp = which.min(bss_summary$cp))

## [1] 6

(best_bic = which.min(bss_summary$bic))

## [1] 5

For instance, adjusted-\(R^2\) suggests we use \(\mathcal{M}_{8}\), i.e. the model with 8 predictor variables.

To reconcile the differences implied by the different model choice criteria, it is helpful to plot how each criterion varies with the number of predictors:

## Create multi-panel plotting device
par(mfrow=c(2,2))
## Produce plots, highlighting optimal value of k
plot(1:p, bss_summary$adjr2, xlab="Number of predictors", ylab="Adjusted Rsq", type="b")
points(best_adjr2, bss_summary$adjr2[best_adjr2], col="red", pch=16)
plot(1:p, bss_summary$cp, xlab="Number of predictors", ylab="Cp", type="b")
points(best_cp, bss_summary$cp[best_cp], col="red", pch=16)
plot(1:p, bss_summary$bic, xlab="Number of predictors", ylab="BIC", type="b")
points(best_bic, bss_summary$bic[best_bic], col="red", pch=16)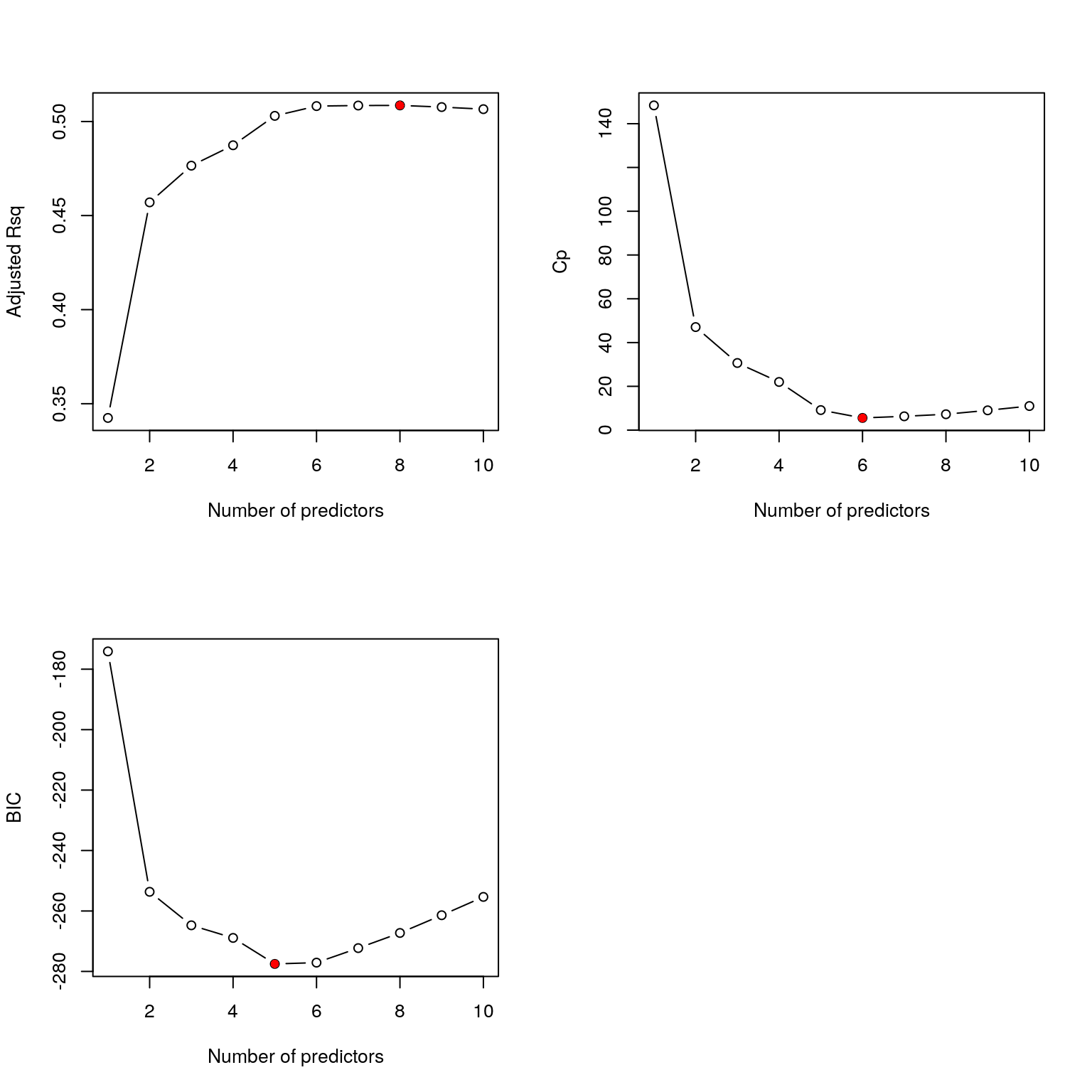

Figure 3.1: Best subset selection for the diabetes data.

In all cases, the optimal point on the graph is at or close to 6 which suggests choosing \(\mathcal{M}_6\). Referring to the output from the summary function, this model uses the variables sex, bmi, map, tc, ldl and ltg. The associated regression coefficients are:

coef(bss_fit, 6)

## (Intercept)         sex         bmi         map          tc         ldl         ltg 
##    152.1335   -226.5106    529.8730    327.2198   -757.9379    538.5859    804.1923

3.3.2 Using \(k\)-fold Cross-Validation to Pick the Number of Predictors

In the previous section, we picked the number of predictors using criteria such as the BIC. An alternative approach is to use the test error estimated using \(k\)-fold cross validation.

To do this, recall that in \(k\)-fold cross validation, each fold defines a split of the data into a validation set (the observations assigned to the fold in question) and a training set (the observations assigned to all other folds). Consider the split implied by fold 1, where the validation data are the observations in fold 1 and the training data are the observations in folds 2 to \(k\). Using these training data, we can apply best-subset selection to identify the best-fitting models with \(1,\ldots,p\) predictors, which we call \(\mathcal{M}_1,\ldots,\mathcal{M}_p\). For each of these \(p\) models, we can then compute the test MSE over the validation data, i.e. the observations in fold 1. We then repeat this procedure for fold 2, then fold 3, and so on. Eventually, we have \(k\) estimates of the test MSE for models with 1 predictor, which we average to get the overall test MSE for models with 1-predictor. Similarly, we have \(k\) estimates of the test MSE for models with 2 predictors, which we average to get the overall test MSE for models with 2-predictors. And so on. This ultimately yields a single estimate of the test MSE for models with \(1,2,\ldots,p\) predictors which we can use as another criterion to choose the number of predictors.

Let us represent these ideas in a function:

reg_bss_cv = function(X, y, fold_ind) {
  p = ncol(X)
  Xy = cbind(X, y=y)
  nfolds = max(fold_ind)
  if(!all.equal(sort(unique(fold_ind)), 1:nfolds)) stop("Invalid fold partition.")
  fold_errors = matrix(NA, nfolds, p)
  for(fold in 1:nfolds) {
    # Using all *but* the fold as training data, find the best-fitting models with 1, ..., p
    # predictors, i.e. M_1, ..., M_p
    tmp_fit = regsubsets(y ~ ., data=Xy[fold_ind!=fold,], method="exhaustive", nvmax=p)
    best_models = summary(tmp_fit)$which[,2:(1+p)]
    # Using the fold as test data, find the test error associated with each of M_1,..., M_p
    for(k in 1:p) {
      fold_errors[fold, k] = reg_fold_error(X[,best_models[k,]], y, fold_ind==fold)
    }
  }
  # Find the fold sizes
  fold_sizes = numeric(nfolds)
  for(fold in 1:nfolds) fold_sizes[fold] = length(which(fold_ind==fold))
  # For each of M_0, M_1, ..., M_p, compute the average test error across folds
  test_errors = numeric(p)
  for(k in 1:p) {
    test_errors[k] = weighted.mean(fold_errors[,k], w=fold_sizes)
  }
  # Return the test error for models M_1, ..., M_p
  return(test_errors)
}

In this function, the trickiest part to understand is likely the chunk:

    best_models = summary(tmp_fit)$which[,2:(1+p)]
    # Using the fold as test data, find the test error associated with each of M_1,..., M_p
    for(k in 1:p) {
      fold_errors[fold, k] = reg_fold_error(X[,best_models[k,]], y, fold_ind==fold)
    }

Referring back to the previous section, it should hopefully be clear that the first line in this chunk extracts our \(p \times p\) matrix of booleans where rows 1 to p indicate which predictors are used in models \(\mathcal{M}_1\) to \(\mathcal{M}_p\), respectively. In the body of the loop over k, X[,best_models[k,]] gives a \(n \times k\) matrix of predictor variables containing only the \(k\) predictors in \(\mathcal{M}_k\).

We can now apply the reg_bss_cv function to our diabetes data. We will use 10-fold cross-validation and apply the same fold assignment index (i.e. fold_index) as before:

## Apply the function to the diabetes data
bss_mse = reg_bss_cv(diabetes[,1:10], diabetes[,11], fold_index)
## Identify model with the lowest error
(best_cv = which.min(bss_mse))

## [1] 6

i.e. the model with 6 predictor variables minimises the test MSE.

We can also visualise how the test error varies with the number of predictor variables and add it to our plots for the other model choice criteria:

## Create multi-panel plotting device
par(mfrow=c(2,2))
## Produce plots, highlighting optimal value of k
plot(1:p, bss_summary$adjr2, xlab="Number of predictors", ylab="Adjusted Rsq", type="b")
points(best_adjr2, bss_summary$adjr2[best_adjr2], col="red", pch=16)
plot(1:p, bss_summary$cp, xlab="Number of predictors", ylab="Cp", type="b")
points(best_cp, bss_summary$cp[best_cp], col="red", pch=16)
plot(1:p, bss_summary$bic, xlab="Number of predictors", ylab="BIC", type="b")
points(best_bic, bss_summary$bic[best_bic], col="red", pch=16)
plot(1:p, bss_mse, xlab="Number of predictors", ylab="10-fold CV Error", type="b")
points(best_cv, bss_mse[best_cv], col="red", pch=16)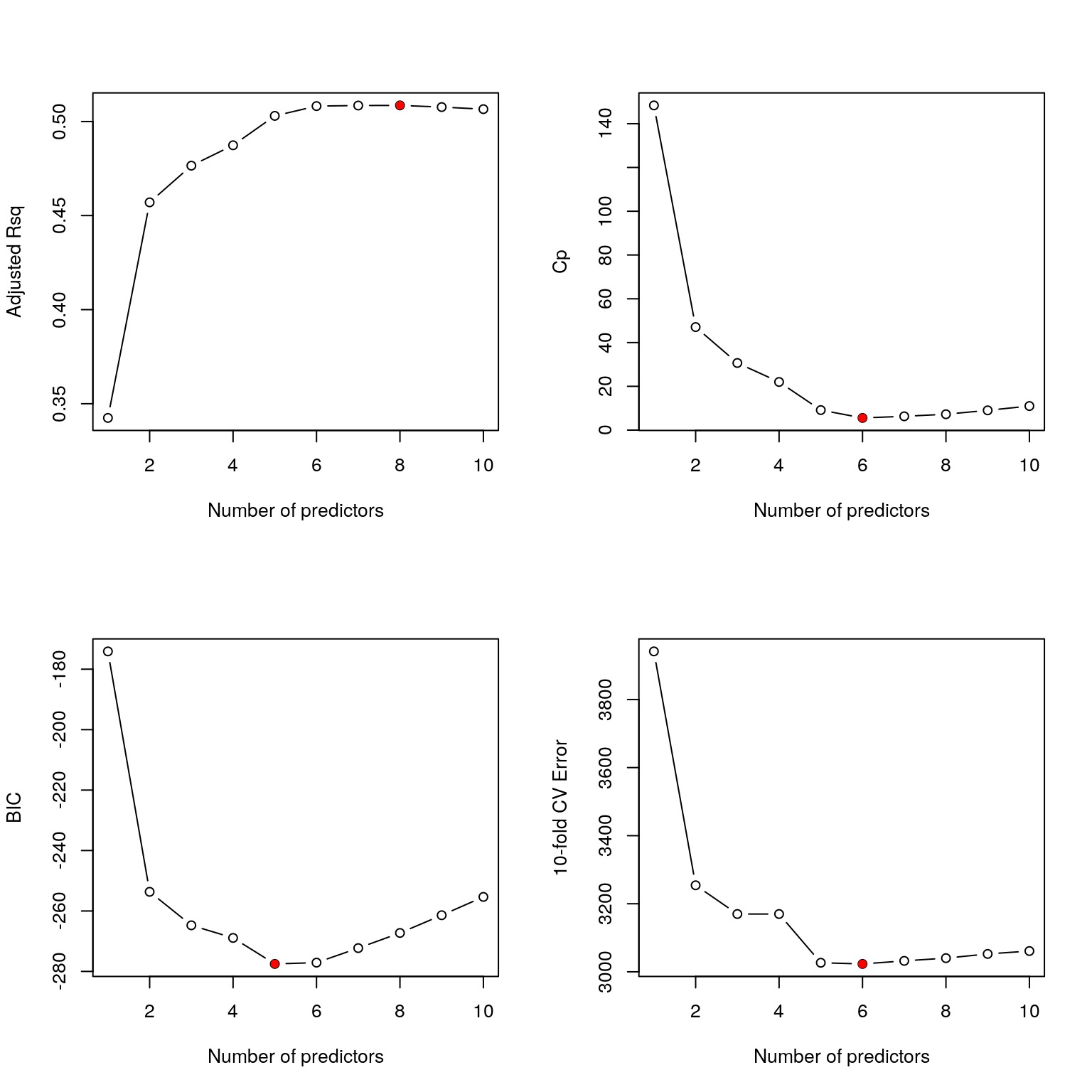

Figure 3.2: Best subset selection for the diabetes data including comparison of 10-fold cross validation errors.

It still seems that a model with 6 predictor variables would be a good choice.

• Repeat the cross-validation exercise above with 8 different randomly sampled fold assignments, i.e. sample the fold_index 8 times, and repeat the calculation of bss_mse each time. You may find it useful to store the results in a \(8 \times 10\) matrix where entry \((i,j)\) is the test MSE for the model with \(j\) predictors based on fold assignment \(i\).
• Plot the estimates of the test error for models with \(1, 2, \ldots,10\) predictors on the same graph, using a different colour for the 8 fold assignments. To this end, remember that you can add points to an existing plot using the points function. Similarly, you can add lines to an existing plot using the lines function.
• Do you see much variation in the estimates of test error across fold assignments?
• Please have a go by yourself before uncovering the solution.

Click for solution

We can sample 8 fold assignments as follows:

## Create matrix to store the fold assignments:
fold_indices = matrix(NA, 8, n)
## Sample the fold assignments:
for(i in 1:8) fold_indices[i,] = sample(k, n, replace=TRUE)

Next we repeat the cross-validation exercise for each fold assignment

## Create a matrix to store the test errors:
bss_mses = matrix(NA, 8, p)
## Calculate the test errors for the p models for each fold assignment:
for(i in 1:8) bss_mses[i,] = reg_bss_cv(diabetes[,1:10], diabetes[,11], fold_indices[i,])
## Identify the best model in each case:
best_cvs = apply(bss_mses, 1, which.min)

Finally, we can plot the results on the same graph:

plot(1:p, bss_mses[1,], xlab="Number of predictors", ylab="10-fold CV Error", type="l")
points(best_cvs[1], bss_mses[1, best_cvs[1]], pch=16)
for(i in 2:8) {
  lines(1:p, bss_mses[i,], col=i)
  points(best_cvs[i], bss_mses[i, best_cvs[i]], pch=16, col=i)
}

We see that there is not a huge amount of variation in the estimates across fold assignments and that most suggest the optimal number of predictors is between 5 and 8, inclusive.