Download Lectures-Workshops-Wk1 Notes

1 Basic Concepts

1.1 Some basic concepts

  • Data consist of information coming from observations, counts, measurements, or responses.

  • Statistics is the science of collecting, organizing, analyzing, and interpreting data in order to make decisions.

  • A population is the collection of all outcomes, responses, measurements, or counts that are of interest. Populations may be finite or infinite. If a population of values consists of a fixed number of these values, the population is said to be finite. If, on the other hand, a population consists of an endless succession of values, the population is an infinite one.

  • A sample is a subset of a population.

  • A parameter is a numerical description of a population characteristic.

  • A statistic is a numerical description of a sample characteristic.

1.2 Branches of statistics

The study of statistics has two major branches - descriptive statistics and inferential statistics:

  • Descriptive statistics is the branch of statistics that involves the organization, summarization, and display of data.

  • Inferential statistics is the branch of statistics that involves using a sample to draw conclusions about a population, e.g. estimation and hypothesis testing.

1.3 What is the idea?

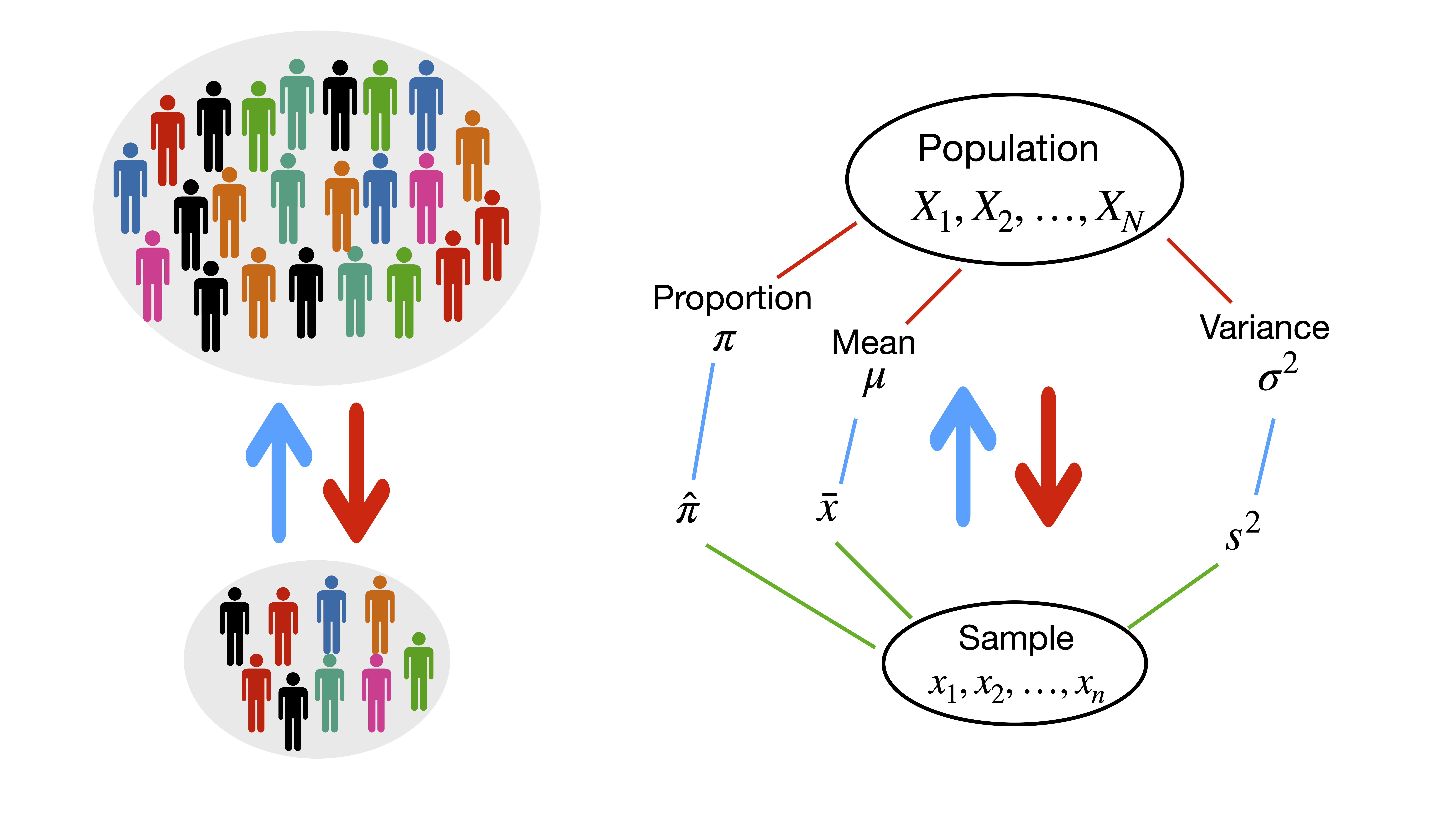
1.4 Notation

  Population Sample
Size \(N\) \(n\)
Parameter Statistic
Mean \(\mu\) \(\bar{x}\)
Variance \(\sigma^2\) \(s^2\)
Standard deviation \(\sigma\) \(s\)
Proportion \(\pi\) \(\hat{\pi}\)
Correlation \(\rho\) \(r\)

2 Data Types in Statistics

2.1 Data collection methods (Traditional data)

There are several ways for collecting data:

  • Take a census: a census is a count or measure of an entire population. Taking a census provides complete information, but it is often costly and difficult to perform.
  • Use sampling: a sample is a count or measure of a part of a population. Statistics calculated from a sample are used to estimate population parameters.
  • Use a simulation: collecting data often involves the use of computers. Simulations allow studying situations that are impractical or even dangerous to create in real life and often save time and money.
  • Perform an experiment: e.g. to test the effect of imposing a new marketing strategy, one could perform an experiment by using the new marketing strategy in a certain region.

2.2 Data collection methods (Big data)

The characteristics of big data (the 4Vs?):

  • Volume: how much data is there?
  • Variety: different types of data?
  • Velocity: at what speed?
  • Veracity: how accurate?

2.3 Types of data

Data sets can consist of two types of data:

  • Qualitative (categorical) data consist of attributes, labels, or nonnumerical entries. e.g. name of cities, gender etc.

  • Quantitative data consist of numerical measurements or counts. e.g. heights, weights, age. Quantitative data can be distinguished as:

    • Discrete data result when the number of possible values is either a finite number or a “countable” number. e.g. the number of phone calls you received in any given day.

    • Continuous data result from infinitely many possible values that correspond to some continuous scale that covers a range of values without gaps, interruptions, or jumps. e.g. height, weight, sales and market shares.

2.4 Types of data (Econometrics)

  • Cross-sectional data: Data on different entities (e.g. workers, consumers, firms, governmental units) for a single time period. For example, data on test scores in different school districts.

  • Time series data: Data for a single entity (e.g. person, firm, country) collected at multiple time periods. For example, the rate of inflation and unemployment for a country over the last 10 years.

  • Panel data: Data for multiple entities in which each entity is observed at two or more time periods. For example, the daily prices of a number of stocks over two years.

2.5 Levels of measurement

  • Nominal: Categories only, data cannot be arranged in an ordering scheme. (e.g. Marital status: single, married etc.)

  • Ordinal: Categories are ordered, but differences cannot be determined or they are meaningless (e.g. poor, average, good)

  • Interval: differences between values are meaningful, but there is no natural starting point, ratios are meaningless (e.g. we cannot say that the temperature 80\(^{\circ}\)F is twice as hot as 40\(^{\circ}\)F)

  • Ratio: Like interval level, but there is a natural zero starting point and rations are meaningful (e.g.  is twice as much as )

3 Descriptive Statistics

3.1 Measures of Central Tendency

Measures of central tendency provide numerical information about a `typical’ observation in the data.

  • The Mean (also called the average) of a data set is the sum of the data values divided by the number of observations.

\[\;\;\;\; \text{Sample mean:}\;\;\; \bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_i\]

  • The Median is the middle observation when the data set is sorted in ascending or descending order. If the data set has an even number of observations, the median is the mean of the two middle observations.
  • The Mode is the data value that occurs with the greatest frequency. If no entry is repeated, the data set has no mode. If two (more than two) values occur with the same greatest frequency, each value is a mode and the data set is called bimodal (multimodal).

3.2 Measure of Variation (Dispersion)

The variation (dispersion) of a set of observations refers to the variability that they exhibit.

  • Range = maximum data value - minimum data value

  • The variance measures the variability or spread of the observations from the mean.

\[\text{Sample variance:}\;\;\;s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2\]

  • Shortcut formula for sample variance is given by \[\text{Sample variance:}\;\;\;s^2=\frac{1}{n-1}\left\{\sum_{i=1}^{n}x^2_i-n\bar{x}^2\right\}\]

  • The standard deviation (\(s\)) of a data set is the square root of the sample variance.

3.3 Shape of a distribution: Skewness

Skewness is a measure of the asymmetry of the distribution.

3.4 Shape of a distribution: Kurtosis

Kurtosis measures the degree of peakedness or flatness of the distribution.

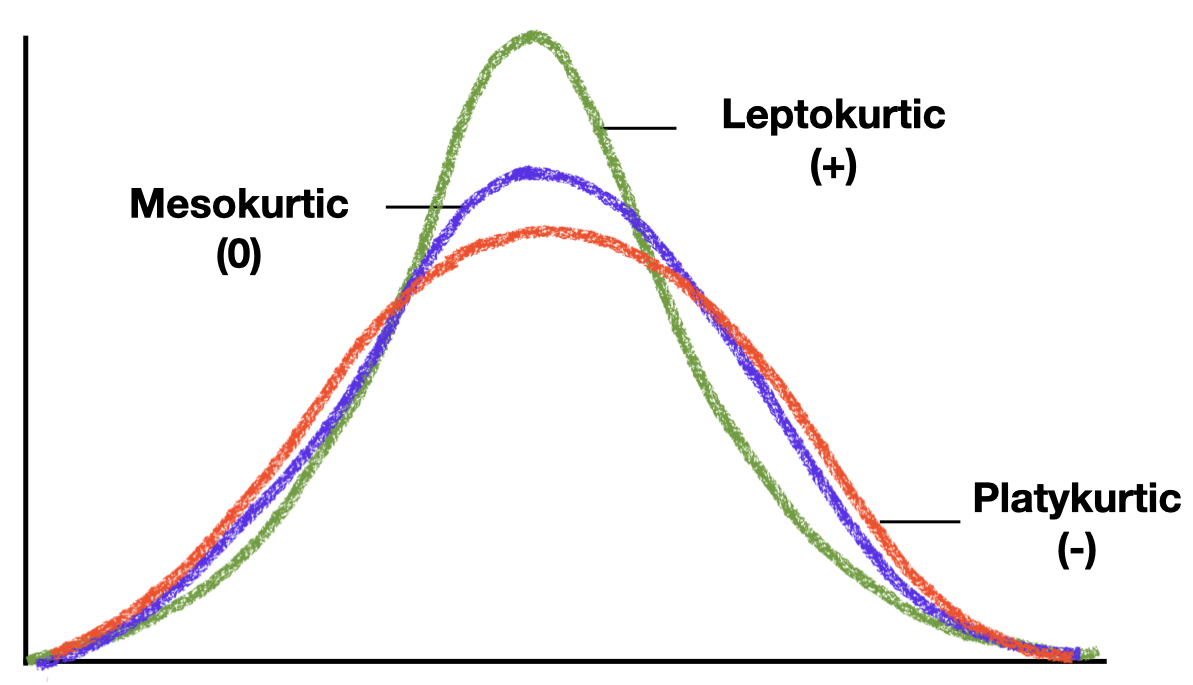
3.5 Modality

3.6 Symmetry

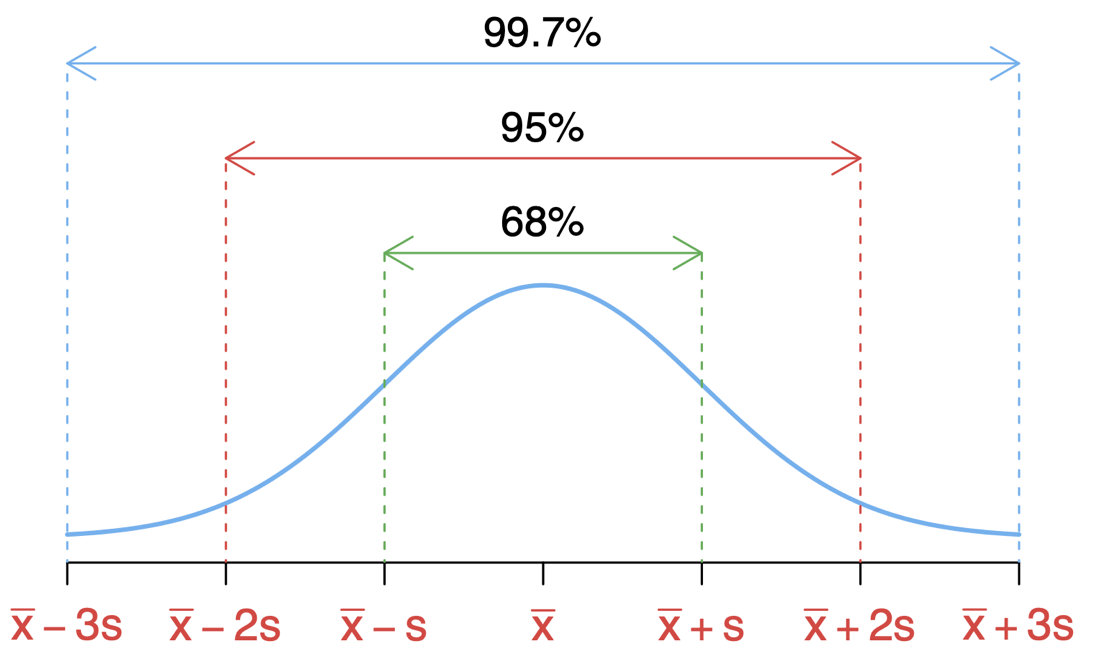
3.7 Empirical Rule

The empirical rule states (for a normally distributed data) that 68% of the data falls within one standard deviation; 95% of the data falls within two standard deviations; 99.7% of the data falls within three standard deviations from the mean.

3.8 Measure of Position: \(z\)-score

The \(z\)-score of an observation tells us the number of standard deviations that the observation is from the mean, that is, how far the observation is from the mean in units of standard deviation.

\[z=\frac{x-\bar{x}}{s}\]

As the \(z\)-score has no unit, it can be used to compare values from different data sets or to compare values within the same data set. The mean of \(z\)-scores is 0 and the standard deviation is 1.

Note that \(s>0\) so if \(z\) is negative, the corresponding \(x\)-value is below the mean. If \(z\) is positive, the corresponding \(x\)-value is above the mean. And if \(z=0\), the corresponding \(x\)-value is equal to the mean.

3.9 Percentiles and Quartiles

  • Given a set of observations, the \(k\)th percentile, \(P_k\) , is the value of \(X\) such that \(k\)% or less of the observations are less than \(P_k\) and \((100-k)\)% or less of the observations are greater than \(P_k\)

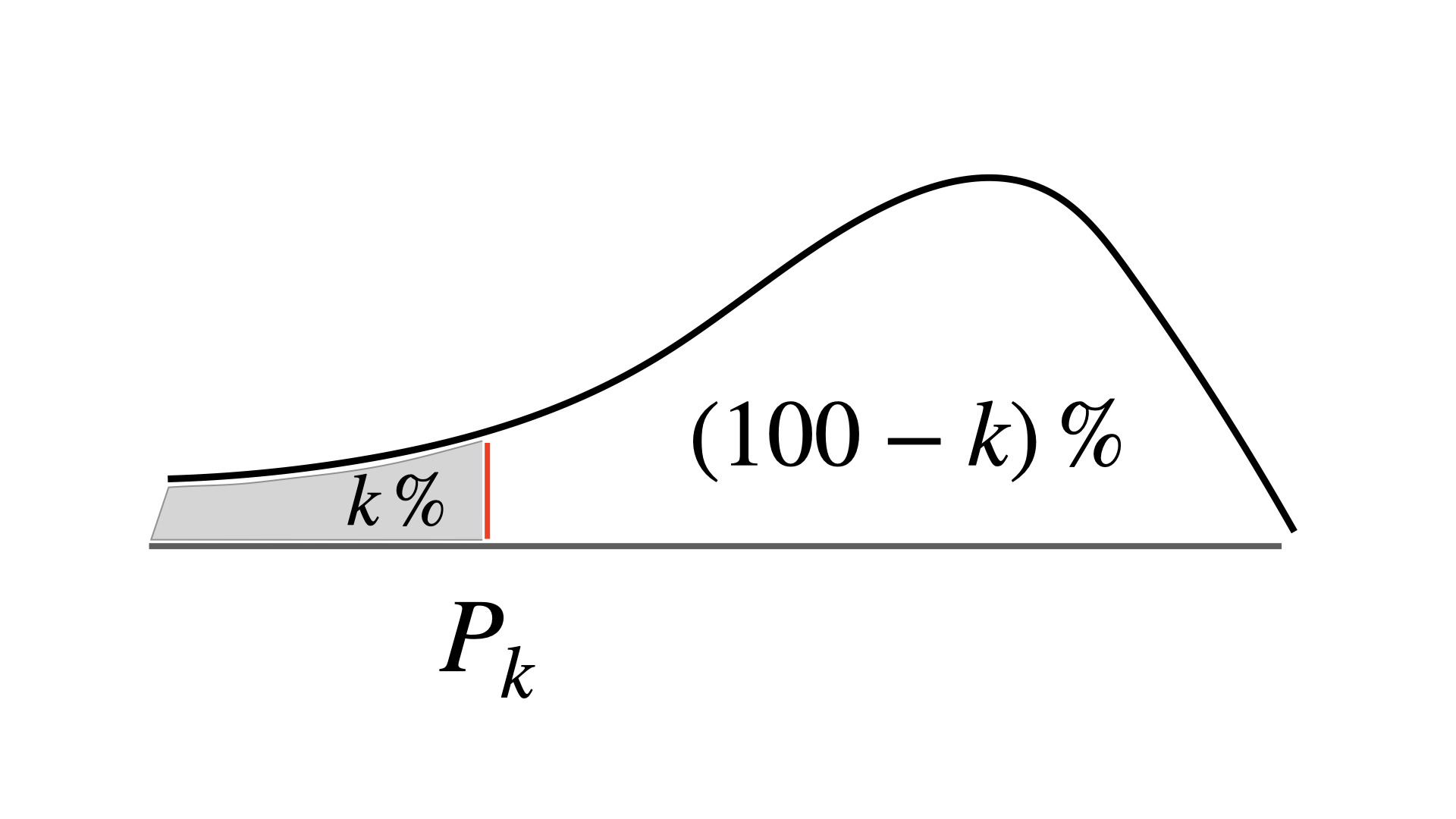
  • The 25th percentile, \(Q_1\), is often referred to as the first quartile.

  • The 50th percentile (the median), \(Q_2\), is referred to as the second or middle quartile.

  • The 75th percentile, \(Q_3\), is referred to as the third quartile

3.9.1 A toy example

3.9.2 The quartiles divide a data set into quarters (four equal parts).

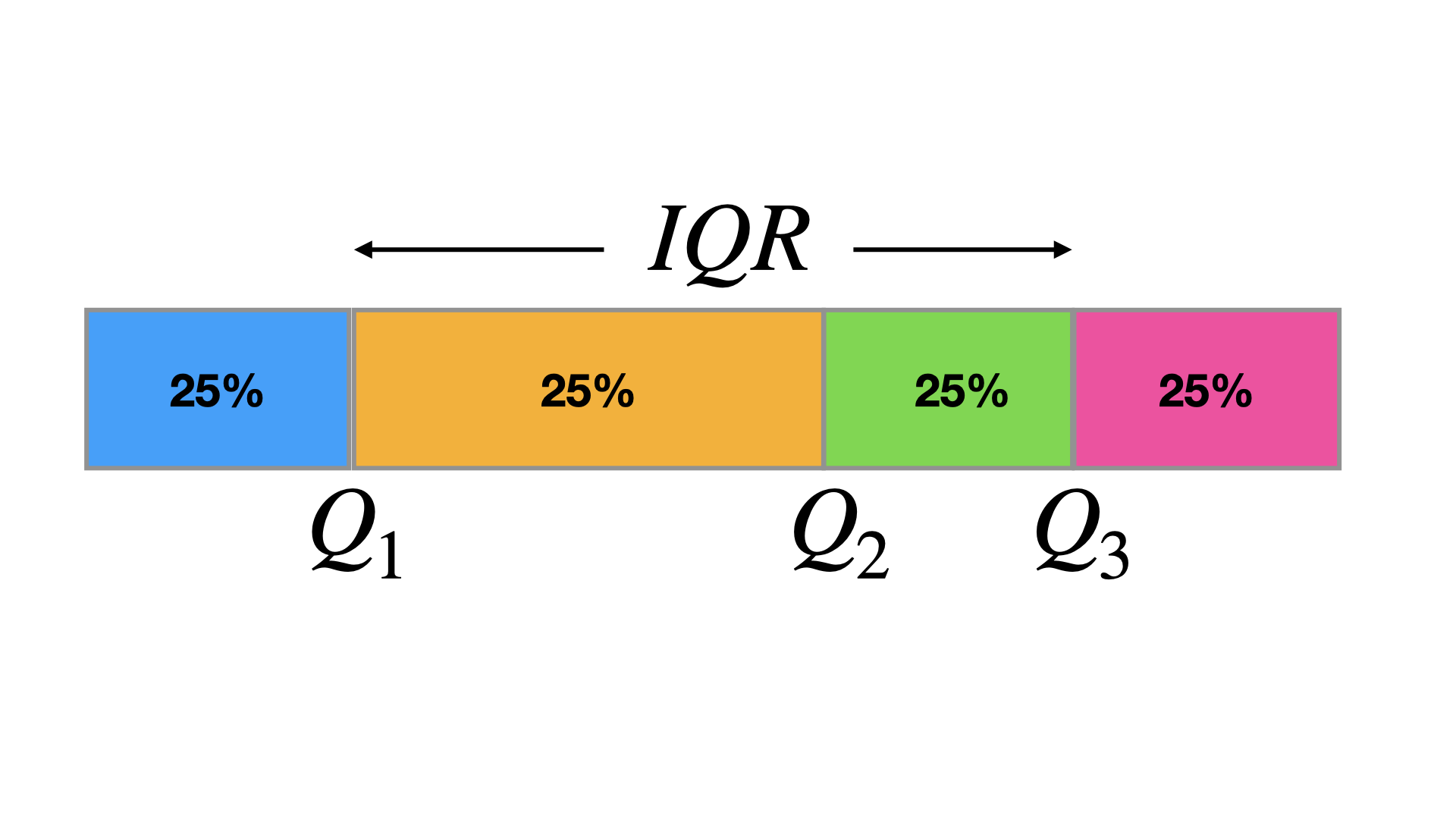
  • The interquartile range (\(IQR\)) of a data set is the difference between the first and third quartiles (\(IQR = Q_3 - Q_1\))

  • The IQR is a measure of variation that gives you an idea of how much the middle 50% of the data varies.

3.10 Five-number summary & Boxplots

To graph a boxplot (a box-and-whisker plot), we need the following values (called the five-number summary):

  • The minimum entry
  • The first quartile \(Q_1\)
  • The median (second quartile ) \(Q_2\)
  • The maximum entry
  • The third quartile \(Q_3\)

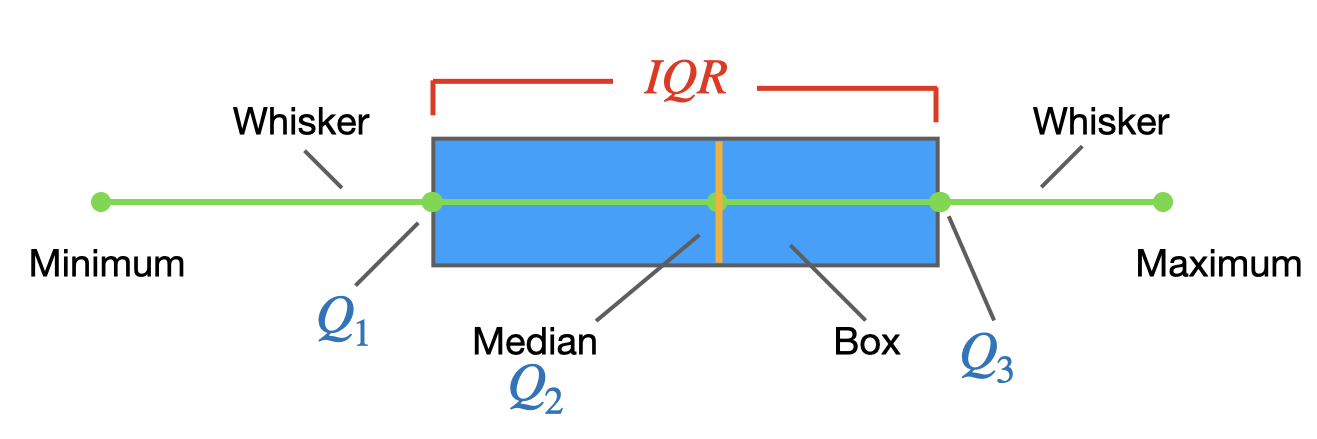The box represents the interquartile range (\(IQR\)), which contains the middle 50% of values.

3.11 Outliers & Extremes values

Some data sets contain outliers or extremes values, observations that fall well outside the overall pattern of the data. Boxplots can help us to identify such values if some rules-of-thumb are used, e.g.:

  • Outlier: Cases with values between 1.5 and 3 box lengths (the box length is the interquartile range) from the upper or lower edge of the box.

  • Extremes: Cases with values more than 3 box lengths from the upper or lower edge of the box.

3.12 Descriptive statistics for qualitative variables

  • Frequency distributions are tabular or graphical presentations of data that show each category for a variable and the frequency of the category’s occurrence in the data set. Percentages for each category are often reported instead of, or in addition to, the frequencies.

  • The Mode can be used in this case as a measure of central tendency.

  • Bar charts and Pie charts are often used to display the results of categorical or qualitative variables. Pie charts are more useful for displaying results of variables that have relatively few categories, in that pie charts become cluttered and difficult to read if variables have many categories.

3.13 Example: Accounting final exam grades

The accounting final exam grades of 10 students are: 88, 51, 63, 85, 79, 65, 79, 70, 73, and 77. Their study programs, respectively, are: MA, MA, MBA, MBA, MBA, MBA, MBA, MSc, MSc, and MSc.

  • The sample mean grade is \[\bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_i=\frac{1}{10}(88+51+\ldots+77)=73\]

  • Next we arrange the data from the lowest to the largest grade: 51, 63, 65, 70, 73, 77, 79, 79, 85, 88. The median grade is 75, which located midway between the 5th and 6th ordered data points \((73+77)/2=75\).

  • The mode is 79 since it appears twice and all other grades appeared only once.

  • The range is \(88-51=37\).

  • The variance \[s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2=\frac{1}{9}((88-73)^2+\ldots+(77-73)^2)=123.78\]

  • The standard deviation: \(s=\sqrt{123.78}=11.13\)

  • The coefficient of variation: \(CV=s/\bar{x}=11.13/73=0.1525\)

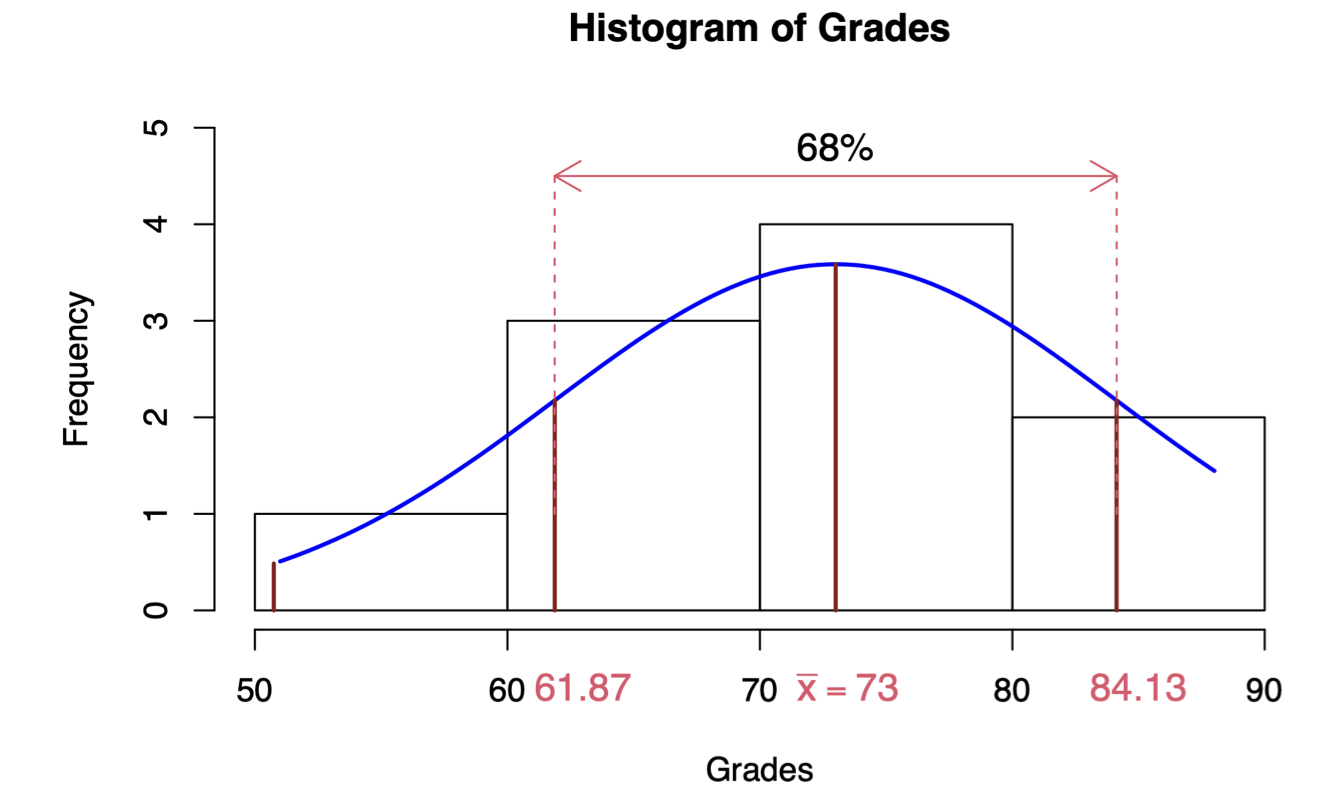
  • Empirical rule: the empirical rule states (for a normally distributed data) that 68% of the data falls within one standard deviation from the mean. In our example, this means that 68% of the grades fall between 61.87 and 84.13 (\(73\pm 11.12555\))

\(~\)

# R codes for "Accounting final exam grades" example
# Data example
grades<-c(88,51,63,85,79,65,79,70,73,77)
program<-factor(c("MA","MA","MBA","MBA","MBA","MBA","MBA","MSc","MSc","MSc"))

# no of observations    
length(grades)
## [1] 10
# Mean, Median, Variance, standard deviation, range, quantile
mean(grades)
## [1] 73
median(grades)
## [1] 75
var(grades)
## [1] 123.7778
sd(grades)
## [1] 11.12555
range(grades)
## [1] 51 88
quantile(grades,probs=c(0,0.25,0.5,0.75,1))
##    0%   25%   50%   75%  100% 
## 51.00 66.25 75.00 79.00 88.00
# Summary
summary(grades)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   51.00   66.25   75.00   73.00   79.00   88.00
# Calculate z-score
(grades-mean(grades))/sd(grades)
##  [1]  1.3482484 -1.9774310 -0.8988323  1.0785987  0.5392994 -0.7190658  0.5392994 -0.2696497  0.0000000  0.3595329
scale(grades)
##             [,1]
##  [1,]  1.3482484
##  [2,] -1.9774310
##  [3,] -0.8988323
##  [4,]  1.0785987
##  [5,]  0.5392994
##  [6,] -0.7190658
##  [7,]  0.5392994
##  [8,] -0.2696497
##  [9,]  0.0000000
## [10,]  0.3595329
## attr(,"scaled:center")
## [1] 73
## attr(,"scaled:scale")
## [1] 11.12555

\(~\)

#  Histograms present frequencies for values grouped into interval.
hist(grades,xlab="grades", main="Histogram of grades")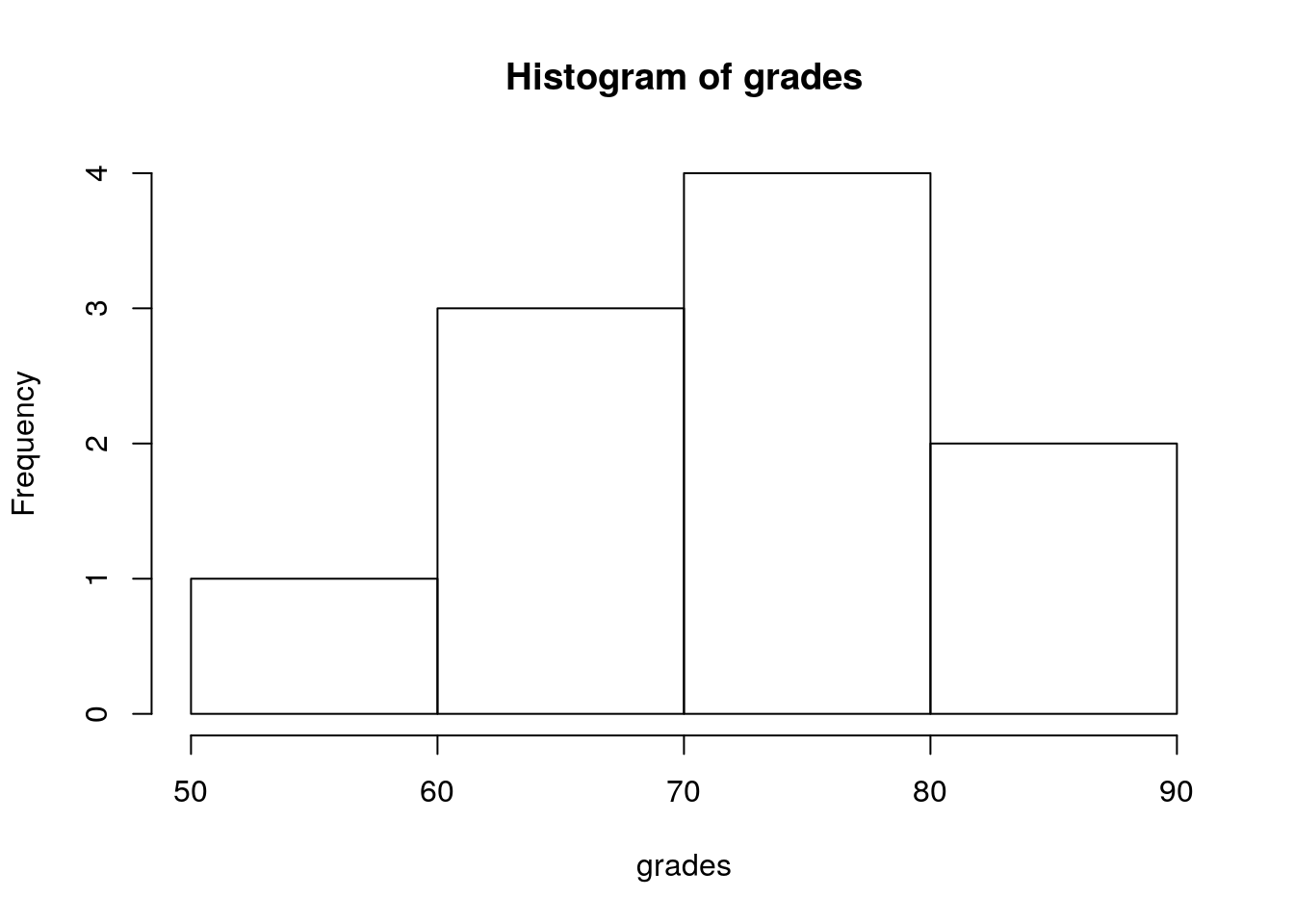

# Boxplot
boxplot(grades,xlab="grades")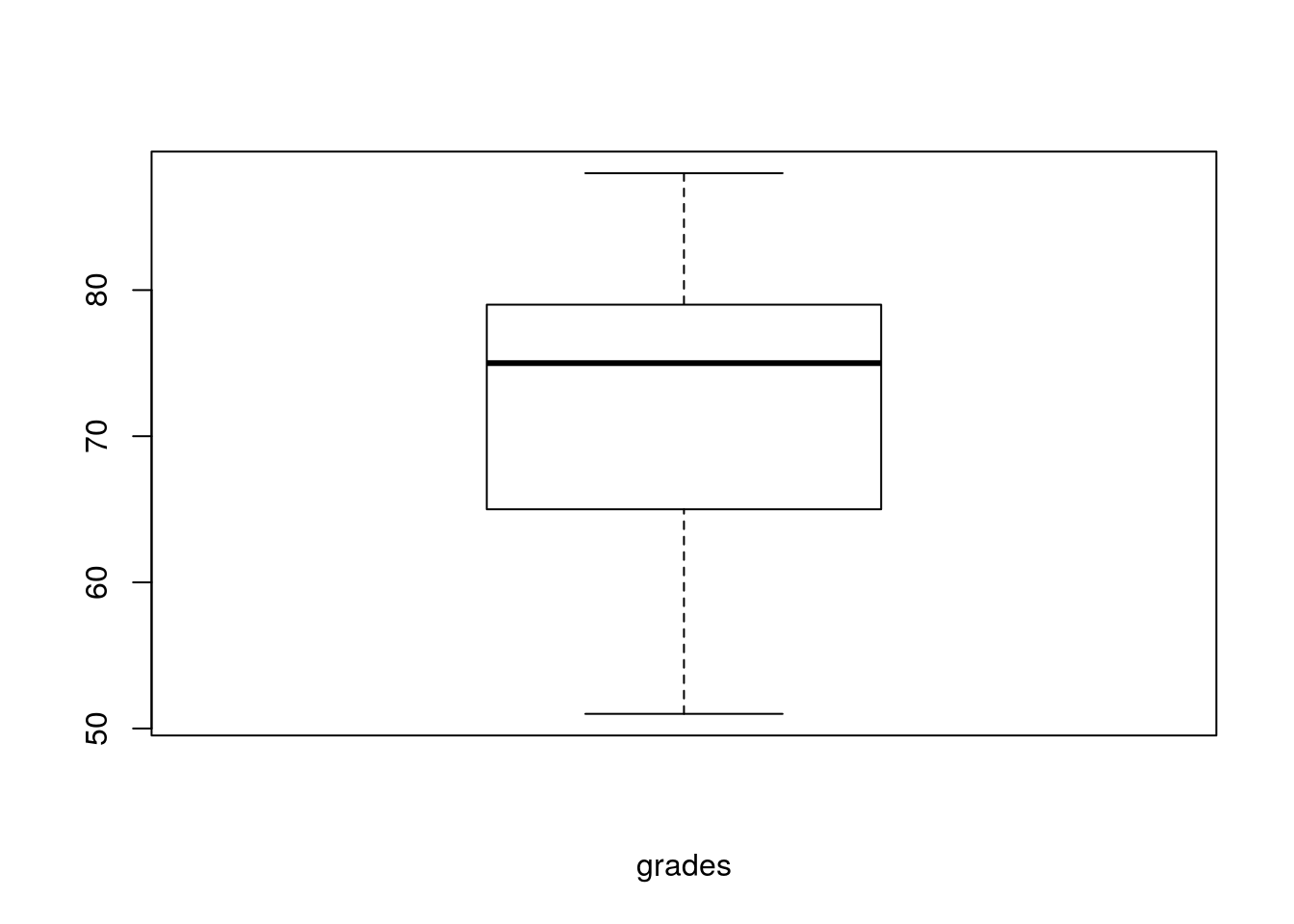

\(~\)

Stem-and-leaf plots: each score on a variable is divided into two parts, the stem gives the leading digits and the leaf shows the trailing digits.

The accounting final exam grades (arranged from the lowest to the largest grade) are: 51, 63, 65, 70, 73, 77, 79, 79, 85, 88.

\(~\)

# Stem-and-leaf plot.
stem(grades)
## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   5 | 1
##   6 | 35
##   7 | 03799
##   8 | 58

Dot plot: is a simple graph to show the relative positions of the data points.

col2<-as.character(factor(program,labels=c("red","blue","orange")))
dotchart(grades, labels=factor(1:10), groups=program, pch=16, col=col2, xlab="Grades",xlim=c(45,100))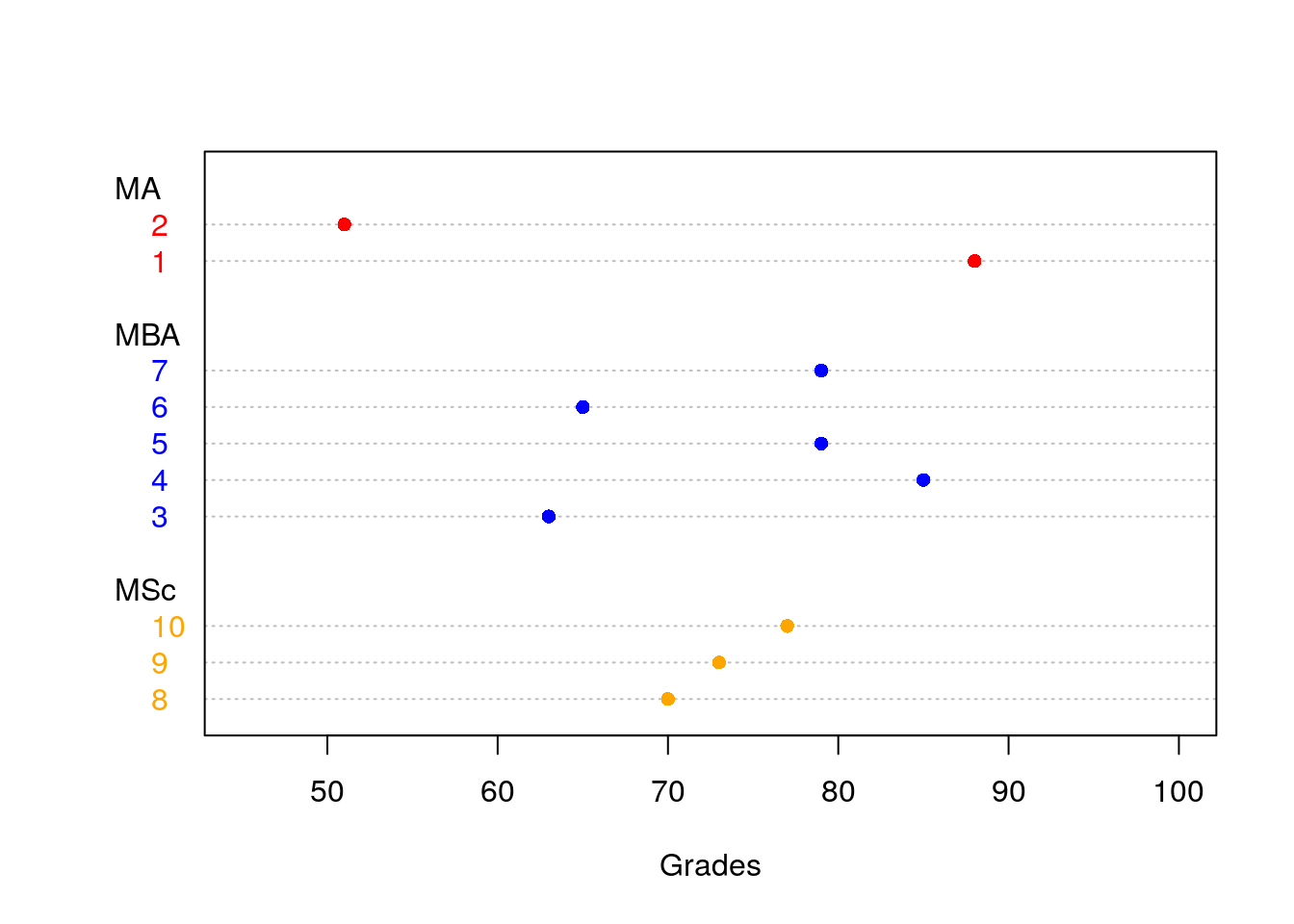

\(~\)

# Frequency table
table(program)
## program
##  MA MBA MSc 
##   2   5   3
# Pie and Bar charts
pie(table(program))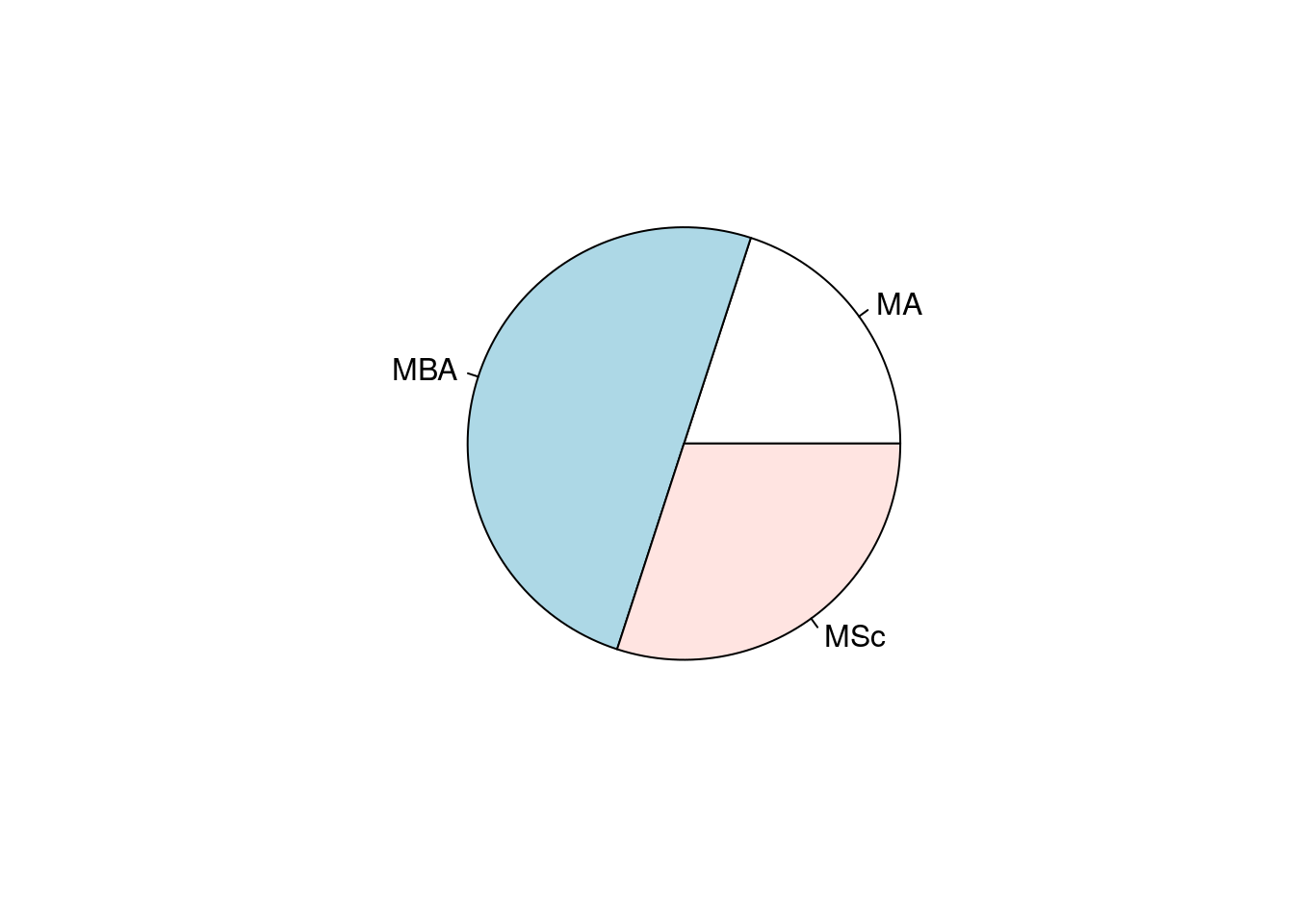

barplot(table(program))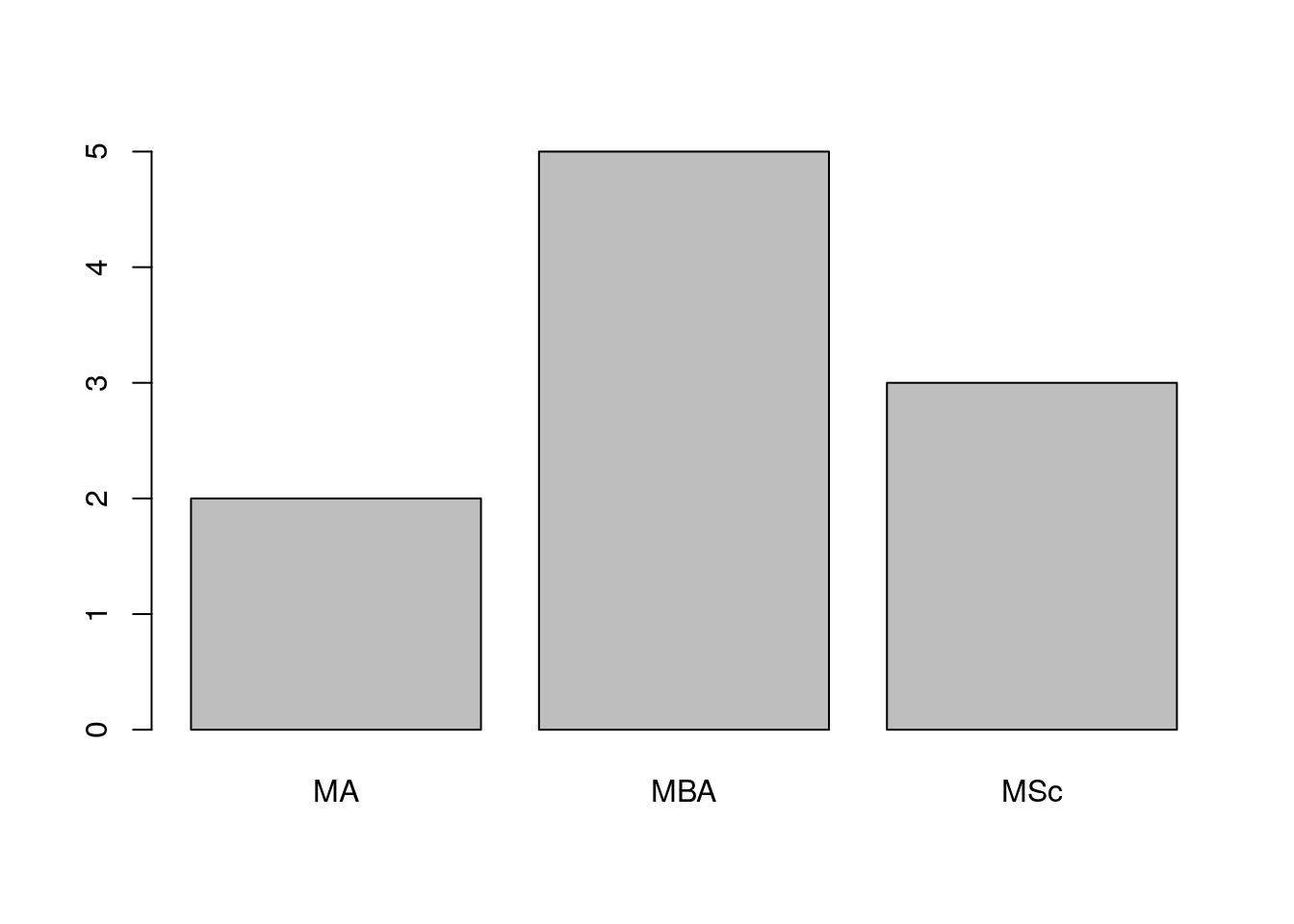

4 Continuous Distributions

4.1 Random Variables

  • A random variable is a variable whose possible values are numerical outcomes of a random experiment.
  • The term `random’ is used here to imply the uncertainty associated with the occurrence of each outcome.
  • Random variables can be either discrete or continuous.
  • A realisation of a random variable is the value that is actually observed.
  • A random variable is often denoted by a capital letter (say \(X\), \(Y\), \(Z\)) and its realisation by a small letter (say \(x\), \(y\), \(z\)).

4.2 Continuous Random Variables

  • For a continuous random variable, the role of the probability mass function is taken by a density function, \(f(x)\), which has the properties that \(f(x) \geq 0\) and \[\int_{-\infty}^{\infty} f (x) dx = 1\]

  • For any \(a < b\), the probability that \(X\) falls in the interval \((a, b)\) is the area under the density function between \(a\) and \(b\): \[P(a < X < b) =\int_{a}^{b} f (x) dx\]

  • Thus the probability that a continuous random variable \(X\) takes on any particular value is 0: \[P(X = c) =\int_c^c f (x) dx = 0\] %Although this may seem strange initially, it is really quite natural. If the uniform random variable of Example A had a positive probability of being any particular number, it should have the same probability for any number in \([0, 1]\), in which case the sum of the probabilities of any countably infinite subset of \([0, 1]\) (for example, the rational numbers) would be infinite.

  • If \(X\) is a continuous random variable, then \[P(a < X < b) = P(a \leq X < b) = P(a < X \leq b)\] Note that this is not true for a discrete random variable.

4.3 Cumulative distribution function

  • The cumulative distribution function (cdf) of a continuous random variable \(X\) is defined as: \[F(x) = P(X \leq x)=\int_{-\infty}^x f (u) du\]

  • The cdf can be used to evaluate the probability that \(X\) falls in an interval: \[P(a \leq X \leq b) = \int_a^b f (x) dx = F(b) - F(a)\]

4.4 Characteristics of probability distributions

  • If X is a continuous random variable with density \(f (x)\), then \[\mu= E(X) =\int_{-\infty}^{\infty}x f (x) dx\] or in general, for any function \(g\), \[E(g(X)) =\int_{-\infty}^{\infty}g(x) f (x) dx\]

  • The variance of \(X\) is \[\sigma^2=Var(X) = E\left\{[X - E(X)]^2\right\}=\int_{-\infty}^{\infty}(x -\mu)^2 f (x) dx\]

  • The variance of \(X\) is the average value of the squared deviation of \(X\) from its mean.

    The variance of \(X\) can also be expressed as \(Var(X)=E(X^2)-[E(X)]^2\) .

4.5 Some useful continuous distributions

4.5.1 Uniform distribution

  • A random variable \(X\) with the density function \[f (x) =\frac{1}{b - a},\; a \leq x \leq b\] is called the uniform distribution on the interval \([a,b]\).

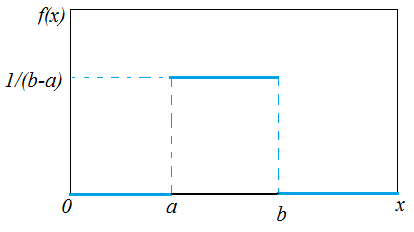
  • The cumulative distribution function is \[F(x)=\left\{\begin{array}{lll}0& \text{for}& x<a\\ \frac{x-a}{b-a}& \text{for}& a\leq x <b \\ 1&\text{for}& x \geq b\end{array}\right.\]

  • A special case, \(f (x) = 1\) and \(0 \leq x \leq 1\).

4.5.2 Exponential distribution

  • The exponential density function is \[f(x)=\lambda e^{-\lambda x},\; x \geq 0 \;\;\text{and}\;\; \lambda >0\]
  • The cumulative distribution function is \[F(x)=\int_{-\infty}^x f(u)du =1-e^{-\lambda x} \]
  • The exponential distribution is often used to model lifetimes or waiting times data.

4.5.3 Normal distribution, \(N(\mu,\sigma^2)\)

  • The normal (Gaussian) distribution plays a central role in probability and statistics, probably the most widely known and used of all distributions
  • The normal distribution fits many natural phenomena, e.g. human’s height, weight, IQ scores. In business, for example, the annual cost of household insurance, among others.
  • The density function of the normal distribution depends on two parameters, \(\mu\) and \(\sigma\) (where \(-\infty < \mu < \infty\), \(\sigma > 0\)): \[f (x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-(x-\mu)^2/2\sigma^2}, -\infty<x<\infty\]
  • The parameters \(\mu\) and \(\sigma\) are the mean and standard deviation of the normal density.
  • We write \(X \sim N(\mu, \sigma^2)\) as short way of saying `\(X\) follows a normal distribution with mean \(\mu\) and variance \(\sigma^2\)’.

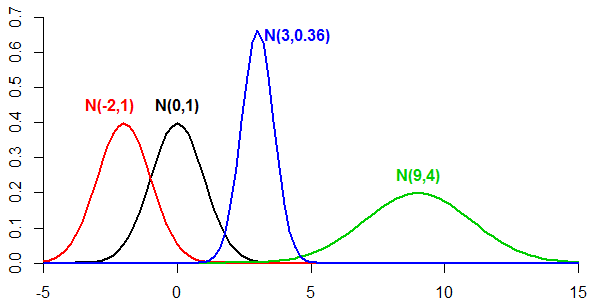
4.5.4 Standard normal distribution \(N(\mu=0,\sigma^2=1)\)

  • The probability density function of the standardized normal distribution is given by:

\[f (z) = \frac{1}{\sqrt{2\pi}} e^{-z^2/2}, -\infty<z<\infty\]

  • We write \(Z \sim N(0,1)\) as short way of saying `\(Z\) follows a standard normal distribution with mean 0 and variance 1’.

  • To standardize any variable \(X\) (into \(Z\)) we calculate \(Z\) as: \[ Z = \frac{X - \mu} { \sigma}\] The \(Z\)-score calculated above indicates how many standard deviations \(X\) is from the mean.

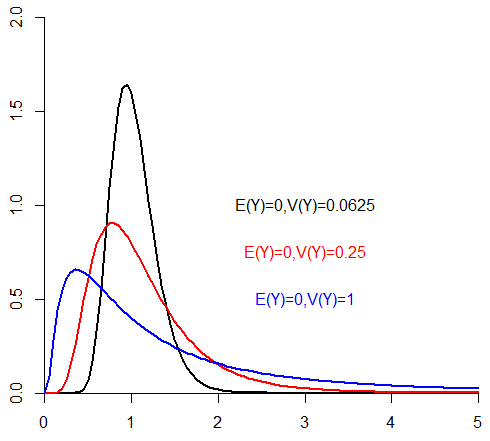
4.5.5 Log-normal distribution and its properties

If \(X\sim N(\mu, \sigma^2)\) then \(Y=e^X\) (\(y \geq 0\)) has a log-normal distribution with mean \(E(Y)=e^{\mu+\sigma^2/2}\) and variance \(V(Y)=(e^{\sigma^2}-1)e^{2\mu+\sigma^2}\).

4.5.6 Distributions derived from the normal distribution

We consider here 3 probability distributions derived from the normal distribution:

  • Chi-square distribution
  • \(T\) or \(t\) distribution
  • \(F\) distribution

These distributions are mainly useful for statistical inference, e.g. hypothesis testing and confidence intervals (to follow).

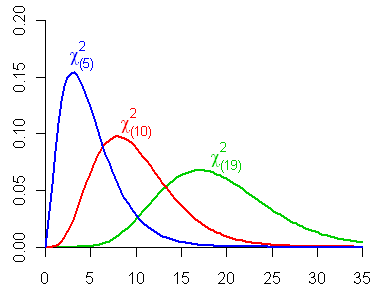
4.5.7 Chi-square distribution, \(\chi^2_{(df)}\)

  • If \(Z\) is a standard normal random variable, the distribution of \(U=Z^2\) is called the chi-square distribution with 1 degree of freedom and is denoted by \(\chi^2_1\).
  • If \(U_1, U_2,\ldots, U_n\) are independent chi-square random variables with 1 degree of freedom, the distribution of \(V=U_1+ U_2+\ldots+ U_n\) is called the chi-square distribution with \(n\) degrees of freedom and is denoted by \(\chi^2_n\).

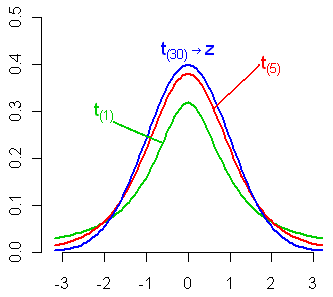
4.5.8 \(T\) distribution, \(t_{(df)}\)

If \(Z \sim N(0,1)\) and \(U \sim \chi^2_n\) and \(Z\) and \(U\) are independent, then the distribution of \(Z/\sqrt{U/n}\) is called the \(t\) distribution with \(n\) degrees of freedom.

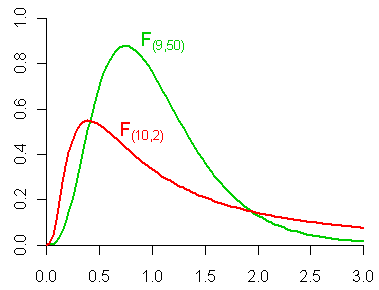
4.5.9 \(F\) distribution, \(F_{(df_1,df_2)}\)

Let \(U\) and \(V\) be independent chi-square random variables with \(m\) and \(n\) degrees of freedom, respectively. The distribution of \[W=\frac{U/m}{V/n}\] is called the \(F\) distribution with \(m\) and \(n\) degrees of freedom and is denoted by \(F_{m,n}\).

4.5.10 Example

  • If \(f_X\) is a normal density function with parameters \(\mu\) and \(\sigma\), then

\[f_Y (y) = \frac{1}{a\sigma\sqrt{2\pi }}exp\left[-\frac{1}{2}\left(\frac{y-b-a\mu}{a\sigma}\right)^2\right]\]

  • Thus, \(Y = aX + b\) follows a normal distribution with parameters \(a \mu + b\) and \(a\sigma\).

  • If \(X \sim N(\mu, \sigma^2)\) and \(Y = aX + b\), then \(Y \sim N(a \mu + b, a^2\sigma^2)\).

  • Can you use this to show that \(Z\sim N(0,1)\)?

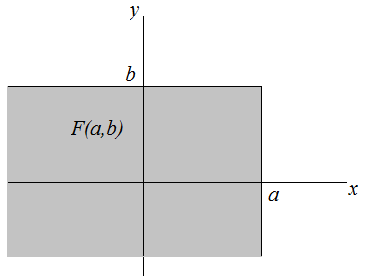
4.6 Joint distribution

  • The joint behaviour of two random variables, \(X\) and \(Y\), is determined by the cumulative distribution function, \[F(x,y)=P(X\leq x, Y \leq y)\] regardless of whether \(X\) and \(Y\) are continuous or discrete. The cdf gives the probability that the point \((X,Y)\) belongs to a semi-infinite rectangle in the plane.

  • The joint density function \(f(x,y)\) of two continuous random variables \(X\) and \(Y\) is such that \[f(x,y) \geq 0\] \[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\;dxdy=1\] \[\int_{c}^{d}\int_{a}^{b}f(x,y)dxdy=P(a \leq X \leq b, c \leq Y \leq d )\] The marginal density function of \(X\) is \[f_X(x)=\int_{-\infty}^{\infty}f(x,y)\;dy\] Similarly, the marginal density function of \(Y\) is \[f_Y(y)=\int_{-\infty}^{\infty}f(x,y)\;dx\]

  • The cdf of two continuous random variables \(X\) and \(Y\) can be obtained as \[F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv\] and \[f(x,y)=\frac{\partial^2}{\partial x \partial y}F(x,y)\] wherever the derivative is defined.

4.7 Conditional probability (density) function, PDF

  • The conditional probability (density) functions may be obtained as follows: \[f_{X|Y}(x|y)=\frac{f(x,y)}{f(y)}\;\;\;\text{conditional PDF of $X$}\] \[f_{Y|X}(y|x)=\frac{f(x,y)}{f(x)}\;\;\;\text{conditional PDF of $Y$}\]
  • Two random variables \(X\) and \(Y\) are statistically independent if and only if \[f(x,y)=f(x)f(y)\] That is, if the joint PDF can be expressed as the product of the marginal PDFs. So, \[f_{X|Y}(x|y)=f(x)\;\;\text{and}\;\;f_{Y|X}(y|x)=f(y)\]

4.8 Properties of Expected values and Variance

  • The expected value of a constant is the constant itself, i.e. if \(c\) is a constant, \(E(c)=c\).

  • The variance of a constant is zero, i.e. if \(c\) is a constant, \(Var(c)=0\).

  • If \(a\) and \(b\) are constants, and \(Y = aX + b\), then \(E(Y)=a E(X)+b\) and \(Var(Y) = a^2Var(X)\) (if \(Var(X)\) exists).

  • If \(X\) and \(Y\) are independent, then \(E(XY) = E(X)E(Y)\) and \[Var(X+ Y)=Var(X) + Var(Y)\] \[Var(X- Y)=Var(X) + Var(Y)\]

  • If \(X\) and \(Y\) are independent random variables and \(g\) and \(h\) are fixed functions, then \[E[g(X)h(Y )] = E[g(X)]E[h(Y )]\]

4.9 Covariance

  • Let \(X\) and \(Y\) be two random variables with means \(\mu_x\) and \(\mu_y\), respectively. Then the covariance between the two variables is defined as \[cov(X,Y)=E\left\{(X-\mu_x)(Y-\mu_y)\right\}=E(XY)-\mu_x\mu_y\]
  • If \(X\) and \(Y\) are independent, then \(cov(X,Y)=0\).
  • If two variables are uncorrelated, that does not in general imply that they are independent.
  • \(Var(X)=cov(X,X)\)
  • \(cov(bX+a, dY+c)=bd\; cov(X,Y)\), where \(a,b,c\), and \(d\) are constants.

4.10 Correlation Coefficient

  • The (population) correlation coefficient \(\rho\) is defined as \[\rho=\frac{cov(X,Y)}{\sqrt{Var(X)Var(Y)}}=\frac{cov(X,Y)}{\sigma_x \sigma_y}\]
  • Thus, \(\rho\) is a measure of linear association between two variables and lies between \(-1\) (indicating perfect negative association) and \(+1\) (indicating perfect positive association).
  • \(cov(X,Y)=\rho \;\sigma_x \sigma_y\)
  • Variances of correlated variables, \[Var(X\pm Y)=Var(X)+Var(Y) \pm 2 cov(X,Y)\] \[Var(X\pm Y)=Var(X)+Var(Y) \pm 2 \rho\; \sigma_x \sigma_y\]

4.11 Conditional expectation and conditional variance

Let \(f(x,y)\) be the joint PDF of random variables \(X\) and \(Y\). The conditional expectation of \(X\), given \(Y=y\), is defined as \[E(X|Y=y)=\sum_x x f_{X|Y}(x|Y=y)\;\;\; \text{if $X$ is discrete}\] \[E(X|Y=y)=\int_{-\infty}^{\infty} x f_{X|Y}(x|Y=y)dx\;\;\; \text{if $X$ is continuous}\] The conditional variance of \(X\) given \(Y=y\) is defined as, if \(X\) is discrete, \[Var(X|Y=y)=\sum_x [X-E(X|Y=y)]^2 f_{X|Y}(x|Y=y)\] and if \(X\) is continuous, \[Var(X|Y=y)=\int_{-\infty}^{\infty} [X-E(X|Y=y)]^2 f_{X|Y}(x|Y=y)dx\]

5 Sampling

5.1 Sampling

  • Sampling is widely used as a means of gathering useful information about a population.
  • Data are gathered from samples and conclusions are drawn about the population as a part of the inferential statistics process.
  • Often, a sample provides a reasonable means for gathering such useful decision-making information that might be otherwise unattainable and unaffordable.
  • Sampling error occurs when the sample is not representative of the population.

5.2 Random versus non-random sampling

  • In random sampling every unit of the population has the same probability of being selected into the sample.

    • Simple random sampling
    • Stratified sampling
    • Cluster sampling
    • Multistage sampling

  • In non-random sampling not every unit of the population has the same probability of being selected into the sample.

    • Convenience sampling
    • Judgement sampling
    • Quota sampling

5.3 Simple random sampling

Simple random sampling: is the basic sampling technique where we select a group of subjects (a sample) from a larger group (a population). Each individual is chosen entirely by chance and each member of the population has an equal chance of being included in the sample.

5.4 Central limit theorem

Let \(X_1, X_2, \ldots\) be independent and identically distributed (i.i.d.) random variables with mean \(\mu\) and variance \(\sigma^2\). Then as \(n\) increases indefinitely (i.e. \(n\rightarrow\infty\)), \(\overline{X}_n=\sum_{i=1}^{n}X_i/n\) approaches the normal distribution with mean \(\mu\) and variance \(\sigma^2/n\). That is \[\overline{X}_n \underset{n\rightarrow\infty}{\sim} N(\mu, \sigma^2/n)\]

Note that this result holds true regardless of the form of the underlying distribution. As a result, it follows that \[Z=\frac{\overline{X}_n-\mu}{\sigma/\sqrt{n}}\underset{n\rightarrow\infty}{\sim} N(0,1)\] That is, \(Z\) is a standardized normal variable.

5.5 Sampling distribution of the sample mean \(\bar{x}\)

The sampling distribution of a statistic is the probability distribution of that statistic.

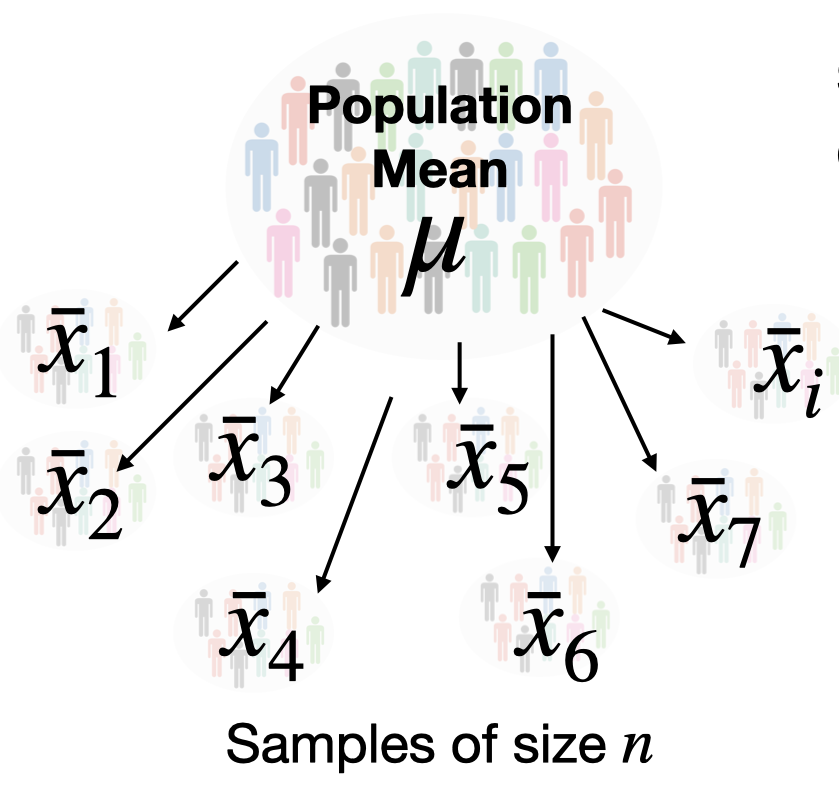
There are two cases:

  1. Sampling is from a normally distributed population with a known population variance: \[\bar{x}\sim N\left(\mu, \frac{\sigma^2}{n}\right) \] That is, the sampling distribution of the sample mean is normal with mean \(\mu_{\bar{x}}=\mu\) and standard deviation \(\sigma_{\bar{x}}=\sigma/\sqrt{n}\).

  2. Sampling is from a non-normally distributed population with known population variance and \(n\) is large, then the mean of \(\bar{x}\), \[\mu_{\bar{x}}=\mu\] and the variance, \[\sigma^2_{\bar{x}}=\left\{\begin{array}{ll} \frac{\sigma^2}{n} & \text{with replacement (infinite population)}\\ &\\ \frac{\sigma^2}{n}\frac{N-n}{N-1} & \text{without replacement (finite population)} \end{array}\right.\]

  • If the sample size is large, the central limit theorem applies and the sampling distribution of \(\bar{x}\) will be approximately normal.

  • The standard deviation of the sampling distribution of the sample mean, \(\sigma_{\bar{x}}\), is called the standard error of the mean or, simply, the standard error

  • If \(\bar{x}\) is a normal distributed (or approximately normal distributed), we can use the following formula to transform \(\bar{x}\) to a \(Z\)-score.

\[Z=\frac{\bar{x}-\mu_{\bar{x}}}{\sigma_{\bar{x}}}\] where \(Z \sim N(0,1)\).

5.6 Sampling distribution of the sample proportion

  • When the sample size \(n\) is large, the distribution of the sample proportion, \(\hat{\pi}\), is approximately normally distributed by the use of the central limit theorem, \[\hat{\pi}\thickapprox N\left(\pi,\frac{\pi(1-\pi)}{n}\right)\] then \[Z=\frac{\hat{\pi}-\pi}{\sqrt{\frac{\pi(1-\pi)}{n}}}\thickapprox N(0,1)\] where \(\hat{\pi}=x/n\), \(x\) is the number in the sample with the characteristic of interest.

  • A widely used criterion is that both \(n\pi\) and \(n(1-\pi)\) must be greater than 5 for this approximation to be reasonable.

5.7 Sampling distribution of the sample variance

Sampling is from a normally distributed population with mean \(\mu\) and variance \(\sigma^2\). The sample variance is \[s^2=\frac{1}{n-1}\sum_{i=1}^{n} (x_i-\bar{x})^2\] and \[E(s^2)=\sigma^2\] \[Var(s^2)= 2\sigma^4/(n-1)\] Then \[\frac{(n-1)s^2}{\sigma^2}\sim \chi^2_{n-1}\]

5.8 Example

Suppose that during any hour in a large department store, the average number of shoppers is 448, with a standard deviation of 21 shoppers. What is the probability that a random sample of 49 different shopping hours will yield a sample mean between 441 and 446 shoppers?

\[\mu =448, \sigma=21, n=49\] \[\begin{align*} P(441\leq \bar{x} \leq 446)=&\left( \frac{441-448}{21/\sqrt{49}}\leq \frac{\bar{x}-\mu}{\sigma/\sqrt{n}}\leq \frac{446-448}{21/\sqrt{49}}\right)\\ P(-2.33 \leq Z \leq -0.67)=&P(Z \leq -0.67)-P(Z \leq -2.33)\\ =&0.2514-0.0099=0.2415 \end{align*}\]

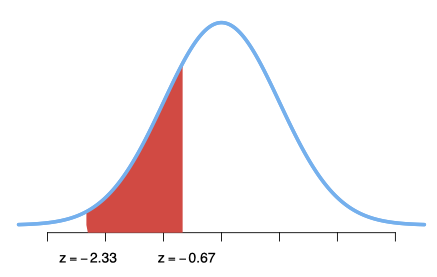That is there is a 24.15% chance of randomly selecting 49 hourly periods for which the sample mean is between 441 and 446 shoppers.

We used the standard normal table to obtain these probabilities. We can also use R.

pnorm(-0.67)-pnorm(-2.33)
## [1] 0.2415258

6 Estimation

6.1 Estimation

  • The values of population parameters are often unknown.
  • We use a representative sample of the population to estimate the population parameters.

There are two types of estimation:

  • Point Estimation
  • Interval Estimation

6.2 Point estimation

  • A point estimate is a single numerical value used to estimate the corresponding population parameter. A point estimate is obtained by selecting a suitable statistic (a suitable function of the data) and computing its value from the given sample data. The selected statistic is called the point estimator.

  • The point estimator is a random variable, so it has a distribution, mean, variance etc.

  • e.g. the sample mean \(\overline{X}=(1/n)\sum_{i=1}^{n}X_i\) is one possible point {} of the population mean \(\mu\), and the point estimate is \(\bar{x}=(1/n)\sum_{i=1}^{n}x_i\).

Properties:

  • Let \(\theta\) be the unknown population parameter and \(\hat{\theta}\) be its estimator. The parameter space is denoted by \(\Theta\).

  • An estimator \(\hat{\theta}\) is called unbiased estimator of \(\theta\) if \(E( \hat{\theta}) = \theta\).

  • The bias of the estimator \(\hat{\theta}\) is defined as \(Bias(\hat{\theta})=E(\hat{\theta})-\theta\)

  • Mean Square Error (MSE) is a measure of how close \(\hat{\theta}\) is, on average, to the true \(\theta\), \[MSE=E[(\hat{\theta}-\theta)^2]= Var(\hat{\theta}) + [Bias (\hat{\theta})]^2\]

6.3 Interval estimation

  • An interval estimate (confidence interval) is an interval, or range of values, used to estimate a population parameter.

  • The level of confidence \((1-\alpha)100\%\) is the probability that the interval estimate contains the population parameter.

  • Interval estimate components:

\[\text{point estimate}\; \pm \; (\text{critical value}\; \times\; \text{standard error})\]

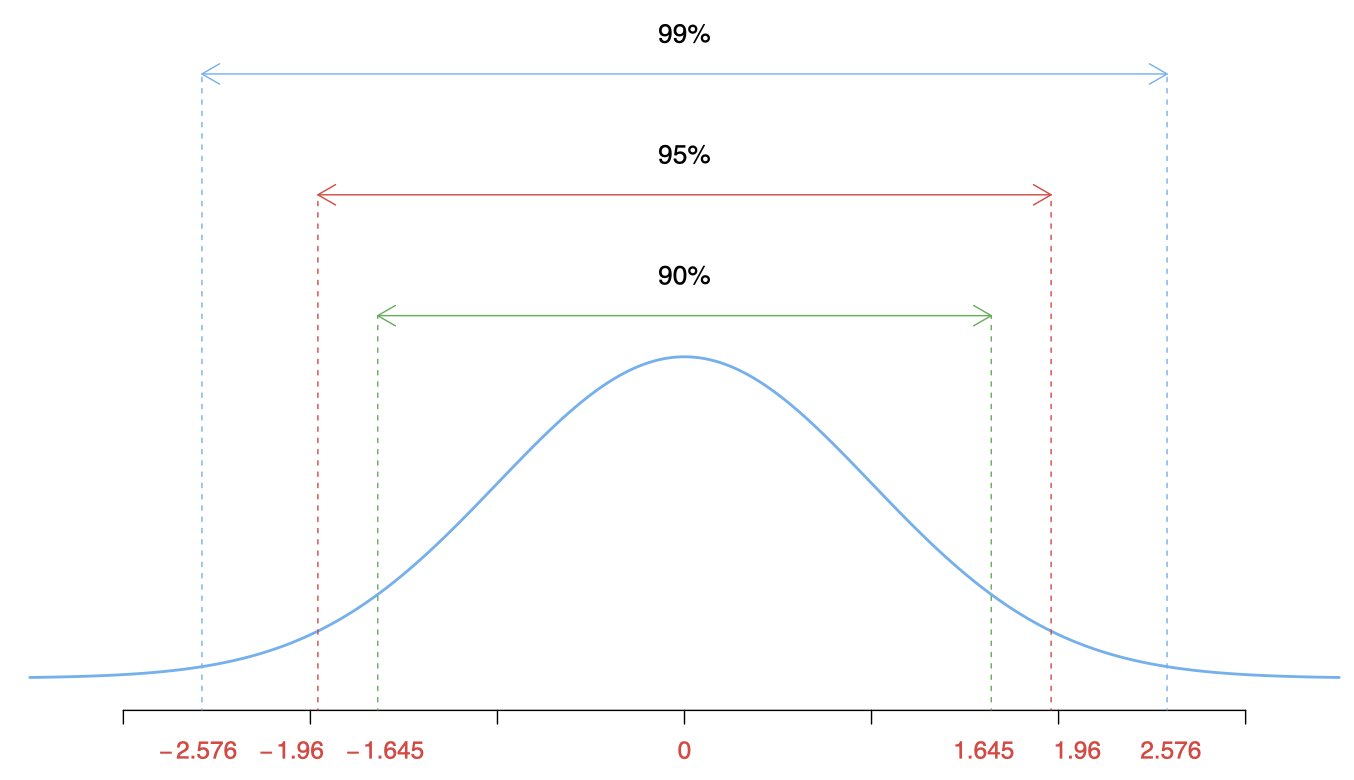
6.4 Confidence intervals for the population mean

  • When sampling is from a normal distribution with known variance \(\sigma^2\), then a \(100(1-\alpha)\%\) confidence interval for the population mean \(\mu\) is \[ \bar{x}\pm z_{\alpha/2} \; (\sigma/\sqrt{n} )\] where \(z_{\alpha/2}\) can be obtained from the standard normal distribution table.

    \(100(1-\alpha)\%\) \(\alpha\) \(z_{\alpha/2}\)
    \(90\%\) 0.10 1.645
    \(95\%\) 0.05 1.96
    \(99\%\) 0.01 2.58

  • If \(\sigma\) is unknown and \(n \geq 30\), the sample standard deviation \(s=\sqrt{\sum(x_i-\bar{x})^2/(n-1)}\) can be used in place of \(\sigma\).

  • If the sampling is from a non-normal distribution and \(n \geq 30\), then the sampling distribution of \(\bar{x}\) is approximately normally distributed (central limit theorem) and we can use the same formula, \(\bar{x}\pm z_{\alpha /2} \; (\sigma /\sqrt{n} )\), to construct the approximate confidence interval for population mean.

  • When sampling is from a normal distribution whose standard deviation \(\sigma\) is unknown and the sample size is small, the \(100(1-\alpha)\%\) confidence interval for the population mean \(\mu\) is \[ \bar{x}\pm t_{\alpha /2} \; (s /\sqrt{n} )\] where \(t_{\alpha/2}\) can be obtained from the \(t\) distribution table with \(df=n-1\) and \(s\) is the sample standard deviation which is given by \[s=\sqrt{\frac{\sum(x_i-\bar{x})^2}{n-1}}\]

  • If \(\sigma\) is unknown, and we neither have normal population nor large sample, then we should use nonparametric statistics (not cover in this course).

6.5 Interpreting confidence intervals

  • Probabilistic interpretation: In repeated sampling, from some population, \(100(1-\alpha)\%\) of all intervals which we constructed will in the long run include the population parameter.

  • Practical interpretation: When sampling is from some population, we have \(100(1-\alpha)\%\) confidence that the single computed interval contains the population parameter.

6.6 Confidence interval for a population proportion

The \(100(1-\alpha)\%\) confidence interval for a population proportion \(\pi\) is given by \[\hat{\pi}\pm z_{\alpha/2} \sqrt{\frac{\hat{\pi}(1-\hat{\pi})}{n}} \] where \(\hat{\pi}\) is the sample proportion.

6.7 Confidence interval for a population variance

The \(100(1-\alpha)\%\) confidence interval for the variance, \(\sigma^2\), of a normally distributed population is given by \[\left(\frac{(n-1)s^2}{\chi^2_{\frac{\alpha}{2}, n-1}}, \frac{(n-1)s^2}{\chi^2_{1-\frac{\alpha}{2}, n-1}}\right)\] where \(s^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar{x})^2\) is the sample variance.

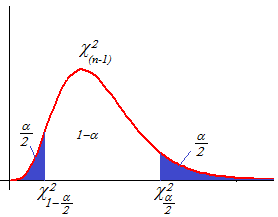
6.8 Example

Suppose a car rental firm wants to estimate the average number of kilometres travelled per day by each of its cars rented in London. A random sample of 20 cars rented in London reveals that the sample mean travel distance per day is 85.5 kilometres, with a population standard deviation of 19.3 kilometres. Compute a 99% confidence interval to estimate \(\mu\).

For a 99% level of confidence, a \(z\) value of 2.58 is obtained (from the standard normal table). Assume that number of kilometres travelled per day is normally distributed.% in the population. \[\bar{x}\pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\] \[85.5 \pm 2.58 \frac{19.3}{\sqrt{20}}\] \[85.5 \pm 11.1\] \[\text{thus}\;\; 74.4 \leq \mu \leq 96.6\]

qnorm((1-0.99)/2)
## [1] -2.575829

7 Hypothesis Testing One Sample

7.1 Hypothesis testing: Motivation

We often encounter such statements or claims:

  • A newspaper claims that the average starting salary of MBA graduates is over 50K. (one sample test)

  • A claim about the efficiency of a particular diet program, the average weight after the program is less than the average weight before the program. (two paired samples test)

  • On average female managers earn less than male managers, given that they have the same qualifications and skills. (two independent samples test)

So we have claims about the populations’ means (averages) and we would like to verify or examine these claims.

This is a kind of problem that hypothesis testing is designed to solve.

7.2 The nature of hypothesis testing

  • We often use inferential statistics to make decisions or judgments about the value of a parameter, such as a population mean.

  • Typically, a hypothesis test involves two hypotheses:

    • Null hypothesis: a hypothesis to be tested, denoted by \(H_0\).
    • Alternative hypothesis (or research hypothesis): a hypothesis to be considered as an alternate to the null hypothesis, denoted by \(H_1\) or \(H_a\).

  • The problem in a hypothesis test is to decide whether or not the null hypothesis should be rejected in favour of the alternative hypothesis.

  • The choice of the alternative hypothesis should reflect the purpose of performing the hypothesis test.

  • How do we decide whether or not to reject the null hypothesis in favour of the alternative hypothesis?

  • Very roughly, the procedure for deciding is the following:

    • Take a random sample from the population.
    • If the sample data are consistent with the null hypothesis, then do not reject the null hypothesis; if the sample data are inconsistent with the null hypothesis, then reject the null hypothesis and conclude that the alternative hypothesis is true.

  • Test statistic: the statistic used as a basis for deciding whether the null hypothesis should be rejected.

  • The test statistic is a random variable which therefore has a sampling distribution with mean and standard deviation (so-called standard error).

7.3 Type I and Type II Errors

  • Type I error: rejecting the null hypothesis when it is in fact true.

  • Type II error: not rejecting the null hypothesis when it is fact false.

  • The significance level, \(\alpha\), of a hypothesis test is defined as the probability of making a Type I error, that is, the probability of rejecting a true null hypothesis.

  • Relation between Type I and II error probabilities: For a fixed sample size, the smaller the Type I error probability, \(\alpha\), of rejecting a true null hypothesis, the larger the Type II error probability of not rejecting a false null hypothesis and vice versa.

  • Possible conclusions for a hypothesis test: If the null hypothesis is rejected, we conclude that the alternative hypothesis is probably true. If the null hypothesis is not rejected, we conclude that the data do not provide sufficient evidence to support the alternative hypothesis.

  • When the null hypothesis is rejected in a hypothesis test performed at the significance level \(\alpha\), we say that the results are statistically significant at level \(\alpha\).

7.4 Hypothesis tests for one population mean

In order to test the hypothesis that the population mean \(\mu\) is equal to a particular value \(\mu_0\), we are going to test the null hypothesis

\[H_0:\mu=\mu_0\]

against one of the following alternatives:

  • \(H_1:\mu\neq\mu_0\) (Two-tailed)
  • \(H_1:\mu<\mu_0\) (Left-tailed)
  • \(H_1:\mu>\mu_0\) (Right-tailed)

In order to test \(H_0\), we need to use one of the following test statistics, we should choose the one that satisfies the assumptions.

  • If \(\sigma\) is known, and we have a normally distributed population or large sample (\(n\geq 30\)), then the test statistic, so-called \(z\)-test, is \[z=\frac{\bar{x}-\mu_0}{\sigma / \sqrt{n}}\] where \(\sigma\) is the standard deviation of the population.
  • If \(\sigma\) is unknown, and we have a normally distributed population or large sample (\(n \geq 30\)), then the test statistic, so-called \(t\)-test, is \[t=\frac{\bar{x}-\mu_0}{s/\sqrt{n}}\;\;\text{with}\;\; df=n-1.\] where \(s\) is the standard deviation of the sample.

7.5 The \(p\)-value approach to hypothesis testing

  • The \(p\text{-value}\) is the smallest significance level at which the null hypothesis would be rejected. The \(p\)-value is also known as the observed significance level.

  • The \(p\text{-value}\) measures how well the observed sample agrees with the null hypothesis. A small \(p\text{-value}\) (close to zero) indicates that the sample is not consistent with the null hypothesis and the null hypothesis should be rejected. On the other hand, a large \(p\text{-value}\) (larger than 0.10) generally indicates a reasonable level of agreement between the sample and the null hypothesis.

  • As a rule of thumb, if \(p \text{-value} \leq \alpha\) then reject \(H_0\); otherwise do not reject \(H_0\).

7.6 Critical-value approach to hypothesis testing

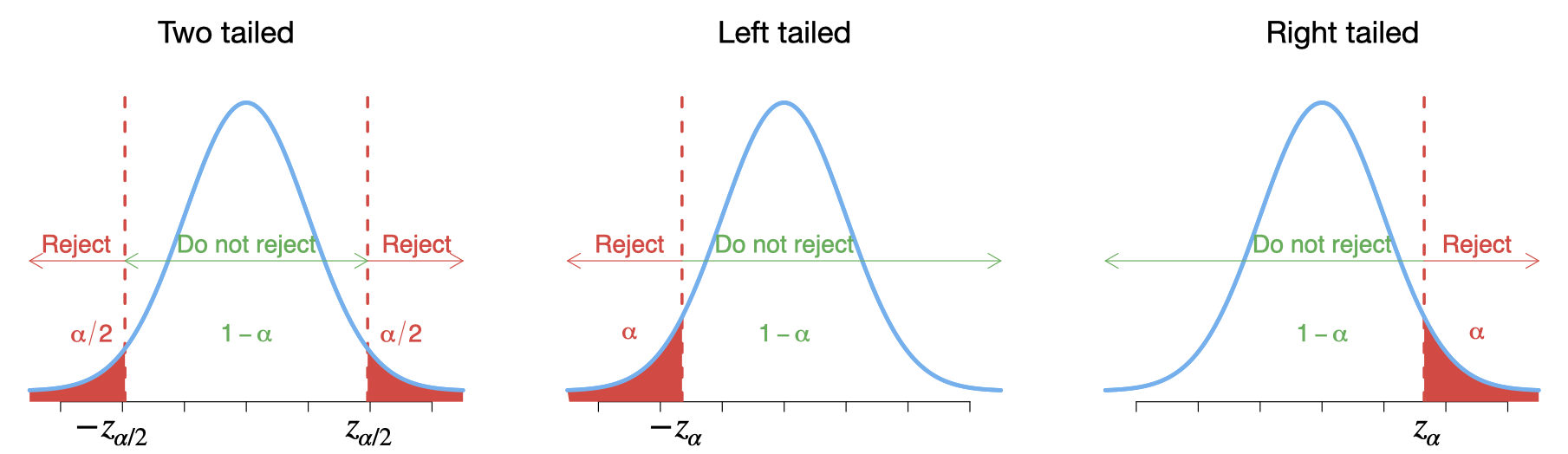
For any specific significance level \(\alpha\), one can obtain these critical values \(\pm z_{\alpha/2}\) and \(\pm z_{\alpha}\) from the standard normal table.

1.282 1.645 1.960 2.326 2.576
\(z_{0.10}\) \(z_{0.05}\) \(z_{0.025}\) \(z_{0.01}\) \(z_{0.005}\)

If the value of the test statistic falls in the rejection region, reject \(H_0\); otherwise do not reject \(H_0\).

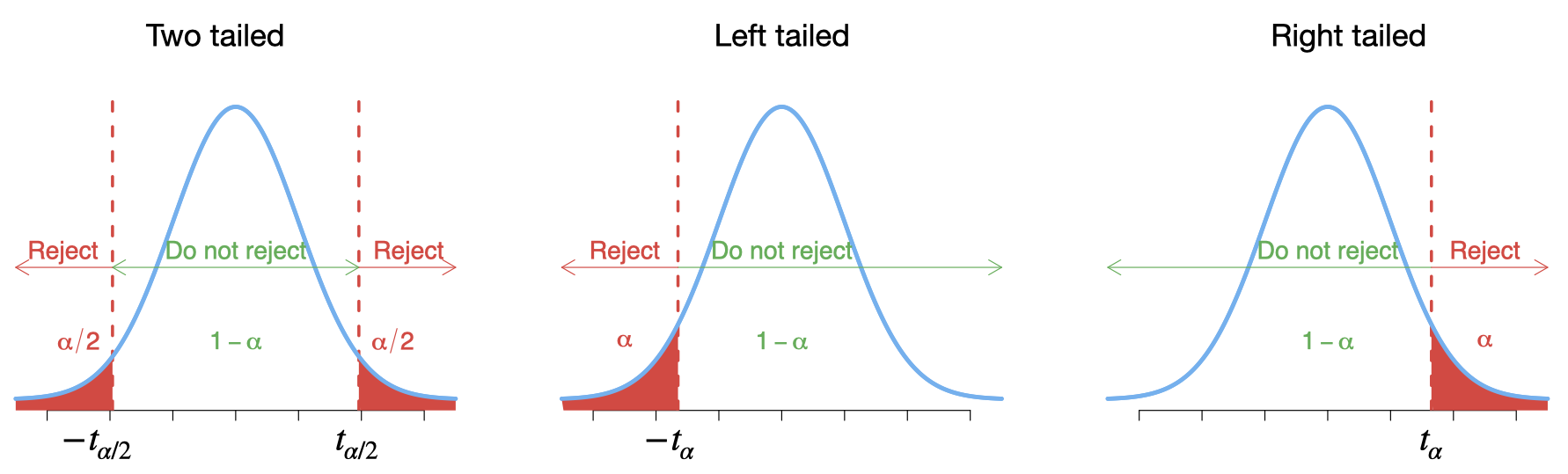
For any specific significance level \(\alpha\), one can obtain these critical values \(\pm t_{\alpha/2}\) and \(\pm t_{\alpha}\) from the T distribution table. For example, for \(df=9\) and \(\alpha=.05\), the critical values are \(\pm t_{0.025}=\pm 2.262\) and \(\pm t_{0.05}=\pm 1.833\).

7.7 Hypothesis testing and confidence intervals

Hypothesis tests and confidence intervals are closely related. Consider, for instance, a two tailed hypothesis test for a population mean at the significance level \(\alpha\). It can be shown that the null hypothesis will be rejected if and only if the value \(\mu_0\) given for the mean in the null hypothesis lies outside the 100(\(1-\alpha\))-level confidence interval for \(\mu\).

Example:

  • At significance level \(\alpha=0.05\), we want to test \(H_0: \mu = 40\) against \(H_1: \mu \neq 40\) (so here \(\mu_0=40\)).
  • Suppose that the 95% confidence interval for \(\mu\) is \(35<\hspace{-1mm}\mu\hspace{-1mm}<38\).
  • As \(\mu_0=40\) lies outside this confidence intervals, we reject \(H_0\).

7.8 Test of Normality

One of the assumptions in order to use \(z\)-test or \(t\)-test is that the population which we sampled from is normally distributed. However we did not yet test this assumption, we should perform a so-called test of normality. In order to do so:

  • We can plot our data sample, e.g. histogram, boxplot, stem-and-leaf and normal Q-Q plot

  • Use normality tests such as Kolmogorov-Smirnov test or Shapiro-Wilk test. The null and alternative hypotheses are:

    • \(H_0\): the population being sampled is normally distributed.
    • \(H_1\): the population being sampled is nonnormally distributed.

If \(\sigma\) is unknown, and we neither have normal population nor large sample, then we should use nonparametric tests instead of \(z\)-test or \(t\)-test (not cover in this course).

7.9 Example

A company reported that a new car model equipped with an enhanced manual transmission averaged 29 mpg on the highway. Suppose the Environmental Protection Agency tested 15 of the cars and obtained the following gas mileages.

27.3 30.9 25.9 31.2 29.7
28.8 29.4 28.5 28.9 31.6
27.8 27.8 28.6 27.3 27.6

What decision would you make regarding the company’s claim on the gas mileage of the car? Perform the required hypothesis test at the 5% significance level.

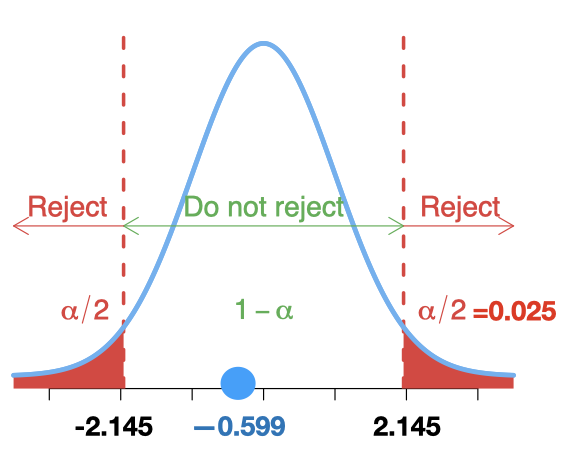
Solution:

The null and alternative hypotheses: \[H_0: \mu =29 \;\text{mpg vs.}\;\;\; H_1: \mu \neq 29\; \text{mpg} \] The value of the test statistic, \[ t=\frac{\bar{x}-\mu _{0} }{s/\sqrt{n} }=\frac{28.753-29}{1.595/\sqrt{15}} =-0.599\] As \(p\)-value \(= 0.559 > \alpha = 0.05\). So, we cannot reject \(H_0\). At the \(5\%\) significance level, the data do not provide sufficient evidence to conclude that the company’s report was incorrect.

R output:

# Data
mlg<-c(27.3, 30.9, 25.9, 31.2, 29.7, 
28.8, 29.4, 28.5, 28.9, 31.6,
27.8, 27.8, 28.6, 27.3, 27.6)

# t-test
t.test(mlg,alternative = "two.sided", mu = 29, conf.level = 0.95)
## 
##  One Sample t-test
## 
## data:  mlg
## t = -0.59878, df = 14, p-value = 0.5589
## alternative hypothesis: true mean is not equal to 29
## 95 percent confidence interval:
##  27.86979 29.63688
## sample estimates:
## mean of x 
##  28.75333
# Normality test
# Kolmogorov Smirnov Test
ks.test(mlg,"pnorm", mean=mean(mlg), sd=sd(mlg))
## Warning in ks.test(mlg, "pnorm", mean = mean(mlg), sd = sd(mlg)): ties should not be present for the Kolmogorov-
## Smirnov test
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  mlg
## D = 0.13004, p-value = 0.9616
## alternative hypothesis: two-sided
# Shapiro-Wilk test
shapiro.test(mlg) 
## 
##  Shapiro-Wilk normality test
## 
## data:  mlg
## W = 0.95817, p-value = 0.6606
par(mfrow=c(1,2))
qqnorm(mlg)
qqline(mlg, col = "red")
hist(mlg)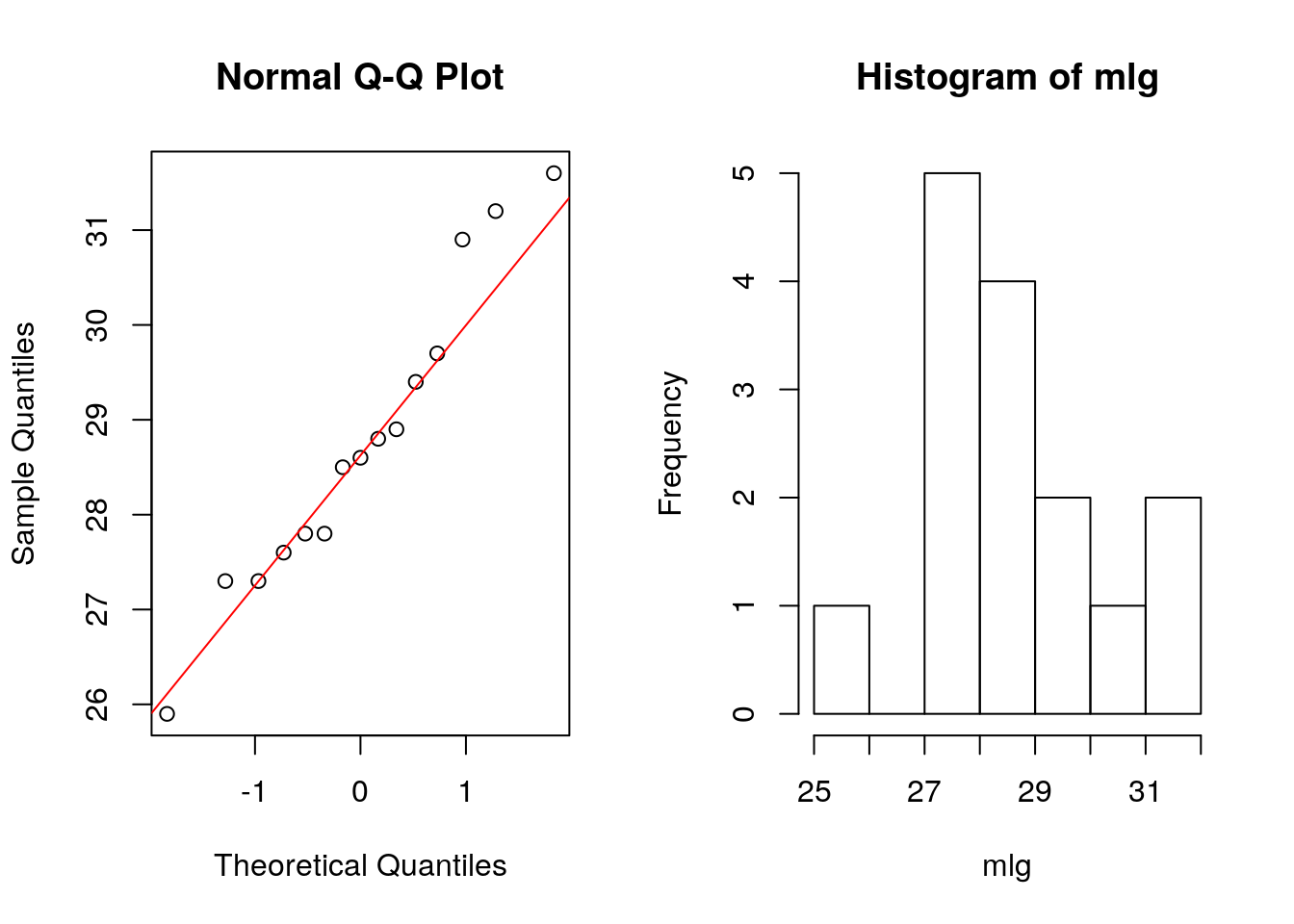

8 Hypothesis Testing Two Samples

8.1 Motivation

We often encounter such statements or claims:

  • A newspaper claims that the average starting salary of MBA graduates is over 50K. (one sample test)

  • A claim about the efficiency of a particular diet program, the average weight after the program is less than the average weight before the program. (two paired samples test)

  • On average female managers earn less than male managers, given that they have the same qualifications and skills. (two independent samples test)

So we have claims about the populations’ means (averages) and we would like to verify or examine these claims.

This is a kind of problem that hypothesis testing is designed to solve.

8.2 Hypothesis tests for two population means

We have two types of samples here:

  • Paired samples: each case must have scores on two variables and it is applicable to two types of studies, repeated-measures (e.g. weights before and after a diet plan) and matched-subjects designs (e.g. measurements on twins or child/parent pairs).

  • Independent samples: two samples are called independent samples if the sample selected from one of the populations has no effect on (holds no information about) the sample selected from the other population.

\(~\)

In order to compare two population means, we are going to test the null hypothesis \[H_{0} :\mu _{1} =\mu _{2} \]

against one of the following alternatives:

  • \(H_1:\mu_1\neq\mu_2\;\) or \(\;\mu_1-\mu_2\neq 0\) (Two-tailed)

  • \(H_1:\mu_1<\mu_2\;\) or \(\;\mu_1-\mu_2< 0\) (Left-tailed)

  • \(H_1:\mu_1>\mu_2\;\) or \(\;\mu_1-\mu_2> 0\) (Right-tailed)

8.4 Comparing two means: Independent samples

In order to test \(H_0:\mu_1=\mu_2\) for two independent samples, we need to use one of the following test statistics, we should choose the one that satisfies the assumptions. Let \(\sigma_1\) and \(\sigma_2\) be the standard deviations of population 1 and population 2, respectively.

8.4.1 z-test

  • Assumptions: \(\sigma_1\) and \(\sigma_2\) are known and we have large samples (\(n_1\geq30\), \(n_2\geq30\))

  • Test statistic: z-test \[z=\frac{\bar{x}_{1} -\bar{x}_{2} }{\sqrt{(\sigma_1^2 /n_1 )+(\sigma_2^2 /n_2 )} } \]

  • \(100(1- \alpha)\%\) confidence intervals for the difference between two population means \(\mu_{1} -\mu_{2}\) are \[(\bar{x}_{1} -\bar{x}_{2} )\pm z_{\alpha /2} \; \sqrt{(\sigma_{1}^{2} /n_{1} )+(\sigma_{2}^{2} /n_{2} )} \]

where \(z_{\alpha/2}\) is the \(\alpha/2\) critical value from the standard normal distribution.

8.4.2 Pooled t-test

  • Assumptions: Normal populations, \(\sigma_1\) and \(\sigma_2\) are unknown but equal (\(\sigma_1 = \sigma_2\))

  • Test statistic: Pooled t-test \[t=\frac{\bar{x}_{1} -\bar{x}_{2} }{s_{p} \; \sqrt{(1/n_{1} )+(1/n_{2} )} } \] has a t-distribution with \(df=n_{1} +n_{2} -2\), where \(s_{p} =\sqrt{\frac{(n_{1} -1)s_{1}^{2} +(n_{2} -1)s_{2}^{2} }{n_{1} +n_{2} -2} }\).

  • \(100(1- \alpha)\%\) confidence intervals for the difference between two population means \(\mu_{1} -\mu_{2}\) are \[(\bar{x}_{1} -\bar{x}_{2} )\pm t_{\alpha /2} \; s_{p} \sqrt{(1/n_{1} )+(1/n_{2} )} \] where \(t_{\alpha/2}\) is the \(\alpha/2\) critical value from the t-distribution with \(df=n_{1} +n_{2} -2\).

8.4.3 Non-Pooled t-test

  • Assumptions: Normal populations, \(\sigma_1\) and \(\sigma_2\) are unknown and unequal (\(\sigma_1 \neq \sigma_2\))

  • Test statistic: Non-Pooled t-test \[t=\frac{\bar{x}_{1} -\bar{x}_{2} }{\sqrt{(s_{1}^{2} /n_{1} )+(s_{2}^{2} /n_{2} )} } \] has a t-distribution with \(df=\Delta=\frac{[(s_{1}^{2} /n_{1} )+(s_{2}^{2} /n_{2} )]^{2} }{\left[\frac{(s_{1}^{2} /n_{1} )^{2} }{n_{1} -1} +\frac{(s_{2}^{2} /n_{2} )^{2} }{n_{2} -1} \right]}\)

  • 100(1- \(\alpha\))% confidence intervals for the difference between two population means \(\mu_{1} -\mu_{2}\) are \[(\bar{x}_{1} -\bar{x}_{2} )\pm t_{\alpha /2} \; \sqrt{(s_{1}^{2} /n_{1} )+(s_{2}^{2} /n_{2} )} \] where \(t_{\alpha/2}\) is the \(\alpha/2\) critical value from the t-distribution with \(df =\Delta\).

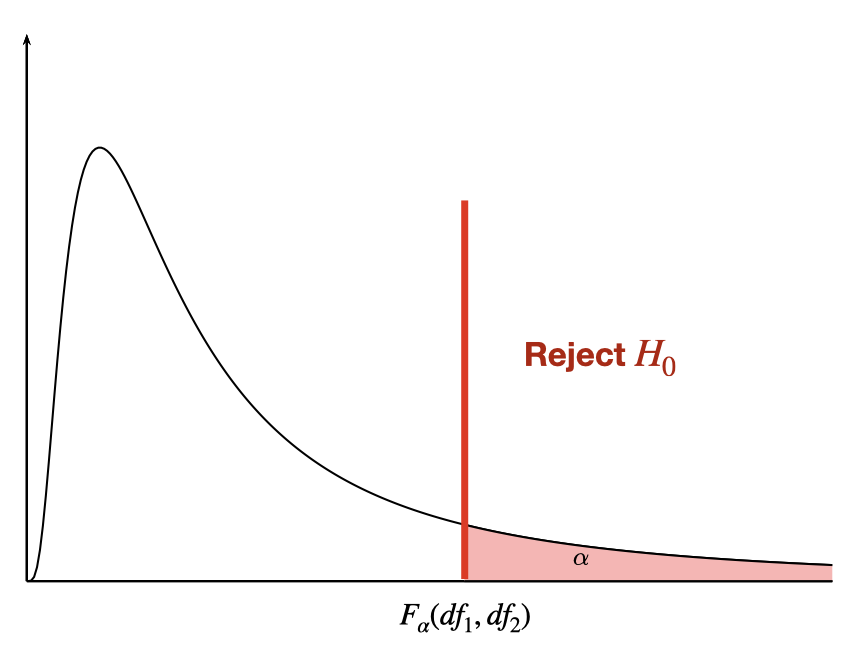
8.4.4 Levene’s Test for Equality of Variances

In order to choose between Pooled t-test and Non-Pooled t-test, we need to check the assumption that the two populations have equal (but unknown) variances. That is, test the null hypothesis that \(H_0:\sigma^2_1=\sigma^2_2\) against the alternative that \(H_1:\sigma^2_1\neq \sigma^2_2\).

The test statistic of Levene’s test follows \(F\) distribution with \(1\) and \(n_1+n_2-2\) degrees of freedoms.

8.5 Critical-value approach to hypothesis testing

  1. State the null and alternative hypotheses

  2. Decide on the significance level \(\alpha\)

  3. Compute the value of the test statistic

  4. Determine the critical value(s)

  5. If the value of the test statistic falls in the rejection region, reject \(H_0\); otherwise do not reject \(H_0\).

  6. Interpret the result of the hypothesis test.

We can replace Steps 4 and 5 by using the p-value. A common rule of thumb is that we reject the null hypothesis if the p-value is less than or equal to the significance level \(\alpha\).

For \(z\)-test:

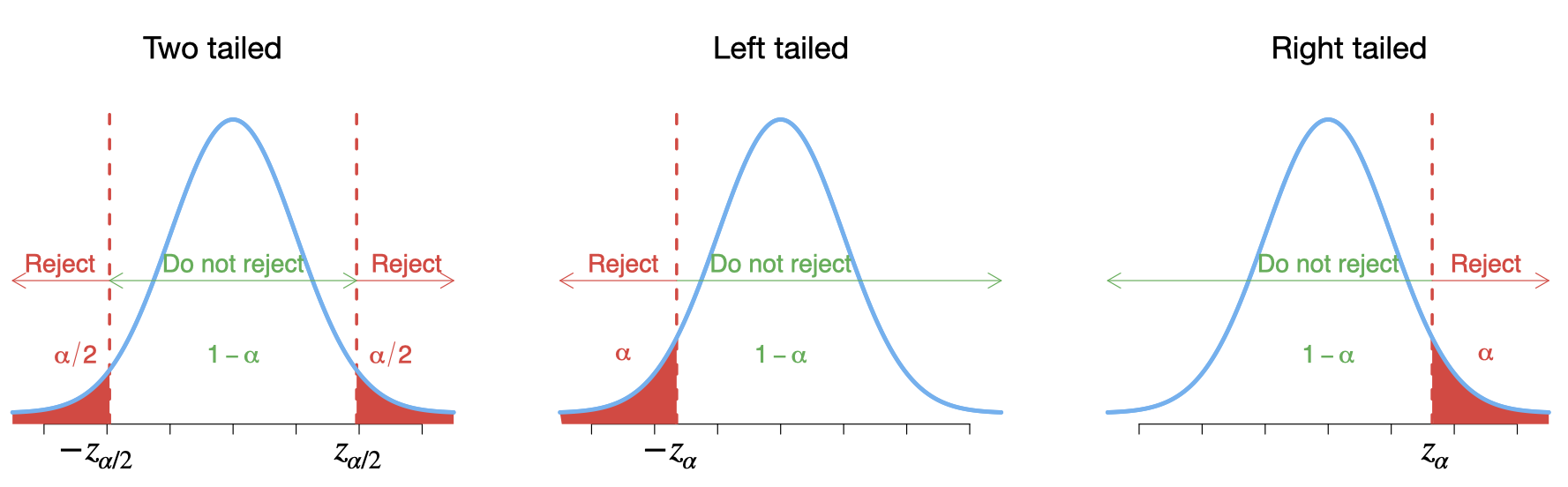
For any specific significance level \(\alpha\), one can obtain these critical values \(\pm z_{\alpha/2}\) and \(\pm z_{\alpha}\) from the standard normal distribution table. If the value of the test statistic falls in the rejection region, reject \(H_0\); otherwise do not reject \(H_0\).

\(z_{0.10}\) \(z_{0.05}\) \(z_{0.025}\) \(z_{0.01}\) \(z_{0.005}\)
1.282 1.645 1.96 0 2.326 2.576

For \(t\)-test:

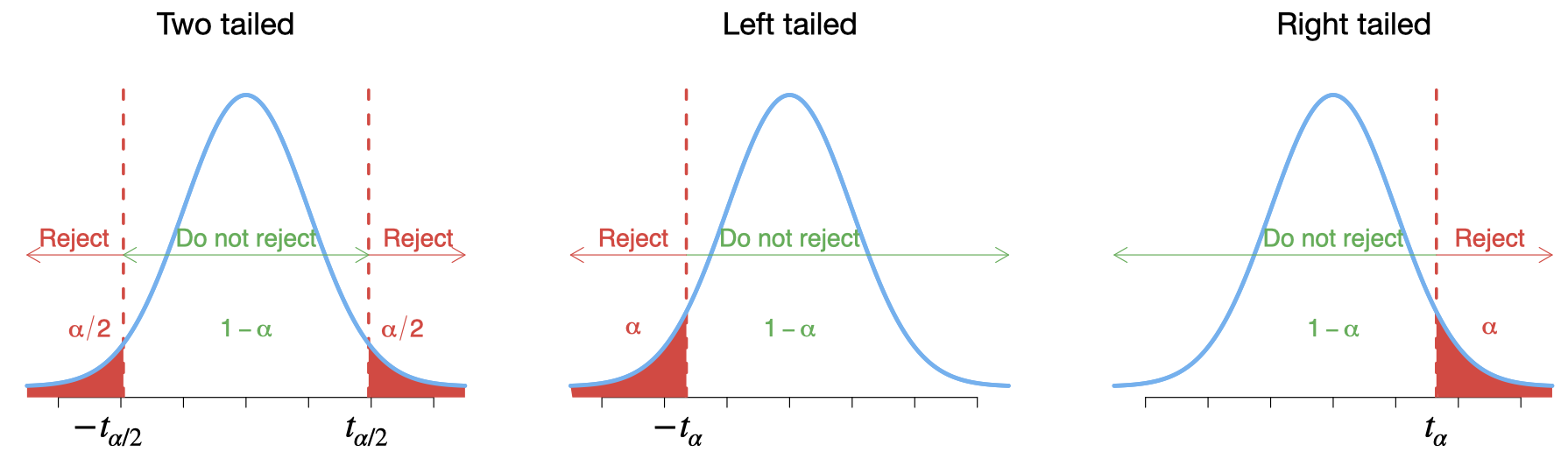
For any specific significance level \(\alpha\), one can obtain these critical values \(\pm t_{\alpha/2}\) and \(\pm t_{\alpha}\) from the T distribution table. For example, for \(df=9\) and \(\alpha=.05\), the critical values are \(\pm t_{0.025}=\pm 2.262\) and \(\pm t_{0.05}=\pm 1.833\).

8.6 Example

In a study of the effect of cigarette smoking on blood clotting, blood samples were gathered from 11 individuals before and after smoking a cigarette and the level of platelet aggregation in the blood was measured. Does smoking affect platelet aggregation?

before after d
25 27 2
25 29 4
27 37 10
44 56 12
30 46 16
67 82 15
53 57 4
53 80 27
52 61 9
60 59 -1
28 43 15

\[\bar{d}=\frac{1}{n}\sum_{i=1}^nd_i=10.27\] \[s_d=7.98\] \[s_{\bar{d}}=\frac{s_d}{\sqrt{n}}=\frac{7.98}{\sqrt{11}}=2.40\]

At the 90% level (\(\alpha=0.10\)), the critical value \(t_{10,0.05}=1.812\), and so a 90% confidence interval is

\[\bar{d}\pm 1.812\;(s_d/\sqrt{n})=10.27\pm1.812\times 2.40=[5.19,14.63]\]

which clearly excludes 0.

To test the null hypothesis that the means before and after are the sample: that is \(H_0:\mu_{before}=\mu_{after}\) against \(H_1:\mu_{before}\neq\mu_{after}\) \[t=\frac{\bar{d}}{s_d/\sqrt{n}}=\frac{10.27}{2.40}=4.28\] since \(|t|>1.812\) then we reject \(H_0\).

before<-c(25,25,27,44,30,67,53,53,52,60,28)
after<-c(27,29,37,56,46,82,57,80,61,59,43)
d<-after-before
qt(0.1/2, df=10)
## [1] -1.812461
t.test(after, before, "two.sided", paired = TRUE,conf.level = 0.90)
## 
##  Paired t-test
## 
## data:  after and before
## t = 4.2716, df = 10, p-value = 0.001633
## alternative hypothesis: true difference in means is not equal to 0
## 90 percent confidence interval:
##   5.913967 14.631488
## sample estimates:
## mean of the differences 
##                10.27273
hist(d,main="",col = '#61B2F2')

qqnorm(d, pch = 1)
qqline(d, col = "steelblue", lwd = 2)

9 Nonparametric Tests

9.1 Wilcoxon signed-rank test (Paired samples)

If the population of all paired differences \(d\) is symmetric but not necessarily normal, then we should use a nonparametric test called Wilcoxon signed-rank test in order to compare the two populations, i.e. to test \(H_0\): no group difference.

To calculate the Wilcoxon signed-rank test statistic:

  • Calculate all paired differences.

  • Rank the absolute differences, that is ignoring the sign, after excluding the zeros.

  • Sum the ranks of the positive and negative differences.

  • The Wilcoxon signed-rank test \(V\) is the minimum of these two sums. That is \[V=\min(V^+,V^-)\] where \(V^+\) is the sum of the ranks of the absolute differences for all pairs with positive difference, and \(V^-\) is the equivalent for negative differences.

  • We can then compare \(V\) to the critical value, \(T\) , for a given significance level, \(\alpha\) , and number of non-zero differences, \(n\), from the statistical table.

  • We reject \(H_0\) at level \(\alpha\) if \(V<T\).

Under \(H_0\) and assuming no ties, \(V\) has the following properties:

  • \(E[V] = \mu_{V} = \frac{1}{4}n(n+1)\).

  • \(Var[V] = \sigma^2_{V} = \frac{1}{24} n(n+1)(2n+1)\).

  • The distribution of \(V\) is symmetric about \(\mu_{V}\).

  • For large \(n\), \(V \sim N(\mu_{V}, \sigma^2_{V})\).

So the standardize version of this test statistic is \[Z=\frac{V-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}\]

9.2 Example

Consider a sample of five students’ grades in Finance and Accounting. We are interested in testing whether the students’ grades in finance is lower than the students’ grades in accounting, so we have a left-tailed test. Use \(\alpha=10\%\).

\(x_1\) \(x_2\) \(x_1-x_2\) rank of \(|x_1-x_2|\)
73 88 -15 3
51 60 -9 2
85 65 20 4
65 66 -1 1
70 70 0 -

The Wilcoxon signed-rank test has value \(V=\min(6,4)=4\).

We compare this value to the critical value \(T=1\) obtained using R, qsignrank(0.1,4), or we can use the p-value as below (using R).

x1<-c(73,51,85,65,70)
x2<-c(88,60,65,66,70)  
wilcox.test(x1,x2,paired=TRUE, alternative = "less") 
## Warning in wilcox.test.default(x1, x2, paired = TRUE, alternative = "less"): cannot compute exact p-value with
## zeroes
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  x1 and x2
## V = 4, p-value = 0.4276
## alternative hypothesis: true location shift is less than 0

\(~\)
As the \(p\)-value is large we do not reject \(H_0\).

\(~\)

9.3 Wilcoxon rank-sum test (Independent samples)

If the two (independent) samples are not normally distributed then we should use a nonparametric test called the Wilcoxon rank-sum test or alternatively the Mann-Whitney U test.

To calculate the Wilcoxon rank-sum test:

  • First combine the two samples into one sample.

  • Rank the combined sample.

  • Calculate the sum of ranks corresponding to the first sample (we can also choose the second sample).

  • Wilcoxon rank-sum test is the sum of ranks of the first sample.

\(~\)

Let the ranks of the first sample in the combined sample be \(r_1,\ldots,r_n\) which are all integers from the set \(\{1,\ldots,N\}\), where \(N=n+m\).

The Wilcoxon rank-sum test statistic is then \[W = \sum_{i=1}^{n} r_i\]

The Mann-Whitney U test statistic is \[W -\frac{n(n+1)}{2}\]

where \(n\) is the number of observations from the first sample, and \(m\) is the number of observations from the second sample.

When the samples are both large, the distribution of the Wilcoxon rank-sum statistic is approximately Normal. For large \(n\) and \(m\), under the null hypothesis of no group differences we have: \[E[W]=\mu_W=\frac{1}{2} n(n+m+1)\] \[Var[W]=\sigma^2_W=\frac{1}{12} nm(n+m+1)\] \[ W\sim N(\mu_W,\sigma^2_W )\] So for large samples, we can use these values to standardise \(W\) and use standard Normal tables to construct confidence intervals and test hypotheses.

9.4 Example

Suppose we have two groups of salaries, in thousand of pounds, of women and men. Test the claim that, on average, women earn less salary than men, so again we have a left-sided test. Use \(\alpha=5\%\)

Women Men
16 18
30 45
25 36
65 28
70 40

  • First we rank the combined sample.

    Combined sample Rank
    16 1
    18 2
    25 3
    28 4
    30 5
    36 6
    40 7
    45 8

  • We will consider women salaries, and the sum of ranks related to the women’s group is \(1+3+5=9\).

  • For \(n=3\), \(m=5\) and \(\alpha=0.05\), we can obtain the critical values from the table, so we have \(T_L=8\) (as we have a left-sided test)

  • Since \(W=9 \nless T_L=8\), so we do not reject \(H_0\).

  • Notice, the value given by R is the Mann-Whitney U test, which is given by

    Mann-Whitney U test= 9 \(- \frac{3(3+1)}{2}=9-6=3\).

\(~\)
Or we can use R as follows:

w<-c(16,30,25)
m<-c(18,45,36,28)  
wilcox.test(w,m, alternative = "less") 
## 
##  Wilcoxon rank sum test
## 
## data:  w and m
## W = 3, p-value = 0.2
## alternative hypothesis: true location shift is less than 0

\(~\)

Again the p-value is large so we do not reject \(H_0\).