This worksheet covers classification methods; the idea is for you to work through it over the course of the three computer labs in the final week of the module. You will receive direction as to which sections to focus on in each lab depending on our progress through the material in the lecture-workshops. The worksheet considers a \(K=2\) group example involving stock-market data. We consider best subset selection for logistic regression, including picking the number of predictors using \(k\)-fold cross-validation, and then a comparison of logistic regression with the Bayes classifiers for LDA and QDA.

1 Background

The Weekly S&P Stock Market Data that we will use in this practical are available as the Weekly data in the ISLR package. It comprises percentage returns for the S&P 500 stock index over 1089 weeks between 1990 and 2010. We begin by loading the data and printing the first few rows

## Load the package
library(ISLR)
## Load the data
data(Weekly)
## Inspect the size
dim(Weekly)

## [1] 1089    9

## Print the first few rows
head(Weekly)

##   Year   Lag1   Lag2   Lag3   Lag4   Lag5    Volume  Today Direction
## 1 1990  0.816  1.572 -3.936 -0.229 -3.484 0.1549760 -0.270      Down
## 2 1990 -0.270  0.816  1.572 -3.936 -0.229 0.1485740 -2.576      Down
## 3 1990 -2.576 -0.270  0.816  1.572 -3.936 0.1598375  3.514        Up
## 4 1990  3.514 -2.576 -0.270  0.816  1.572 0.1616300  0.712        Up
## 5 1990  0.712  3.514 -2.576 -0.270  0.816 0.1537280  1.178        Up
## 6 1990  1.178  0.712  3.514 -2.576 -0.270 0.1544440 -1.372      Down

For each week, the column labelled Today gives the percentage return that week whilst the columns labelled Lag1 up to Lag5 give the percentage returns for one week previous up to five weeks previous. Year is the year in which the observation was recorded and Volume gives the average number of daily shares traded (in billions) that week. Finally, Direction is a factor with two levels – Down and Up – indicating whether the market had a negative or positive return in that week, i.e. if Today\(< 0\) then Direction\(=\)Down, whilst if Today\(\ge 0\) then Direction\(=\)Up. We are interested in whether we can predict whether the market has a negative or positive return for the S&P 500 stock index using its value in previous weeks and the current volume of trading. One way of investigating this question would be to build a multiple linear regression model for Today with Lag1, \(\ldots\), Lag5 and Volume as predictor variables. (Because, clearly, if we can predict percentage returns, we can also predict whether they are negative or positive). However, for the purpose of illustration in this example, we will ignore the Today column and use Direction as our response variable.

Before we begin to analyse the data, note that Direction is stored as a factor:

head(Weekly$Direction)

## [1] Down Down Up   Up   Up   Down
## Levels: Down Up

where Down is the first level and Up the second. Recall that R stores factors internally as integers:

typeof(Weekly$Direction)

## [1] "integer"

head(as.integer(Weekly$Direction))

## [1] 1 1 2 2 2 1

And so Down is represented internally as a 1 and Up as a 2. When working with logistic regression, I prefer to adopt the more standard 0/1 numerical labels. To do this, whilst also omitting the Today column, we can create a new data frame:

## Create new column of 0s and 1s
MyWeekly = data.frame(Weekly[,-(8:9)], Direction=as.integer(Weekly$Direction)-1)
## Print first few rows:
head(MyWeekly)

##   Year   Lag1   Lag2   Lag3   Lag4   Lag5    Volume Direction
## 1 1990  0.816  1.572 -3.936 -0.229 -3.484 0.1549760         0
## 2 1990 -0.270  0.816  1.572 -3.936 -0.229 0.1485740         0
## 3 1990 -2.576 -0.270  0.816  1.572 -3.936 0.1598375         1
## 4 1990  3.514 -2.576 -0.270  0.816  1.572 0.1616300         1
## 5 1990  0.712  3.514 -2.576 -0.270  0.816 0.1537280         1
## 6 1990  1.178  0.712  3.514 -2.576 -0.270 0.1544440         0

So in my labelling 0 and 1 refer to weeks where the stock market is down or up, respectively.

2 Exploratory Data Analysis

Now that we are clear in our labelling of the response variable, we can perform some exploratory data analysis. We note that

table(MyWeekly$Direction)

## 
##   0   1 
## 484 605

and so the stock market was up over more weeks than it was down.

There are various ways we could explore the data graphically. For example, we can get an idea of the relationships between variables by producing a pairs plot of the predictors and, additionally, the year, colouring the points according to whether the stock market was up or down:

pairs(MyWeekly[,1:7], col=MyWeekly[,8]+1)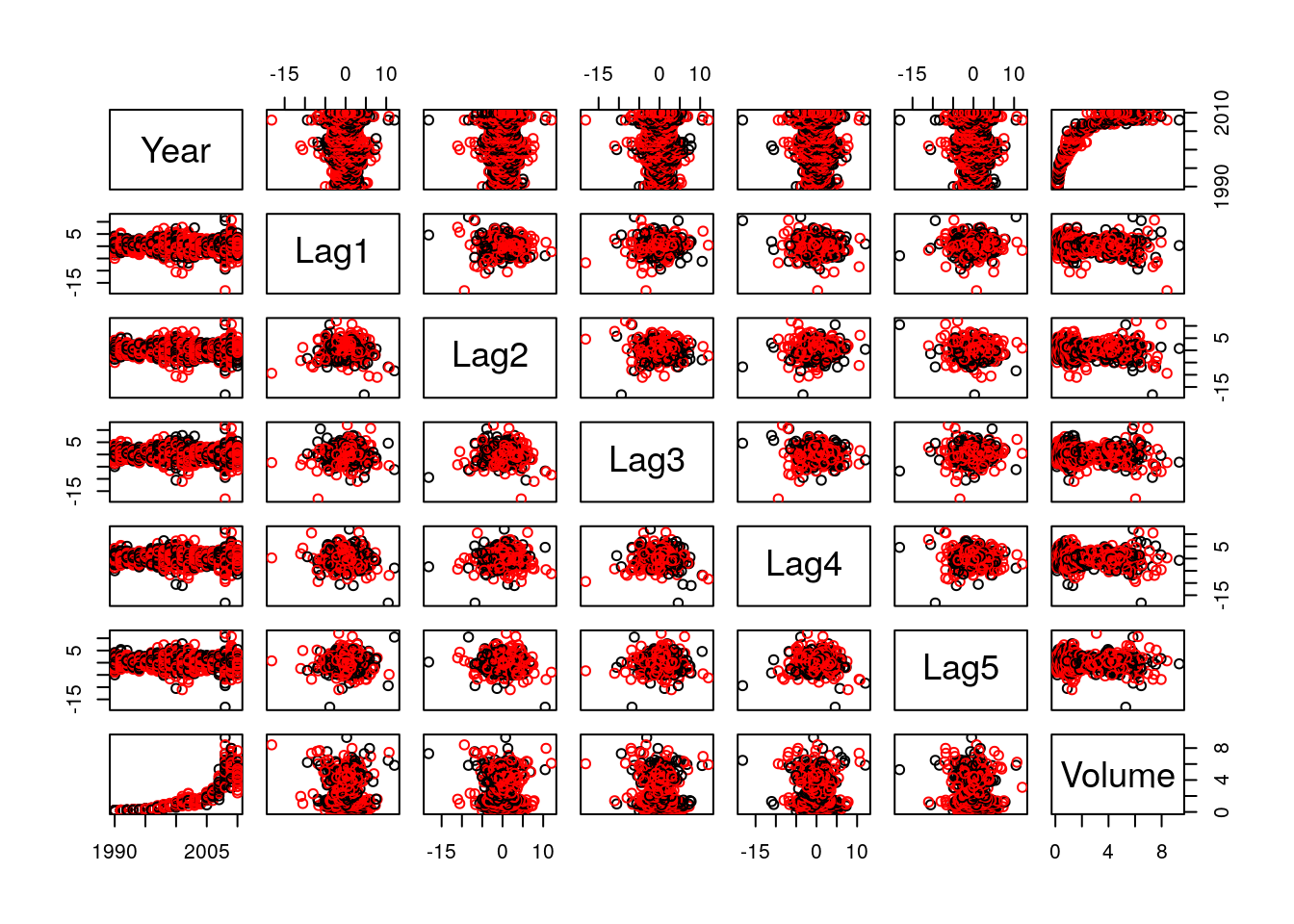

Figure 2.1: Scatterplot for the Weekly data. Weeks when the stock market is down / up appear in black / red.

This produces the plot above. On the basis of this plot the only obvious pattern is the positive, though non-linear, relationship between Volume and Year, which suggests that the overall volume of traded shares is increasing over time. None of the predictors show any obvious relationship with Direction.

3 Logistic Regression

3.1 The Full Model

We start by recording the number of rows in our data frame and the number of predictor variables.

## Store n and p
(n = nrow(MyWeekly))

## [1] 1089

(p = ncol(MyWeekly) - 1)

## [1] 7

Next, we will fit a logistic regression model for Direction in terms of the predictors Lag1 through Lag5 and Volume:

logreg_fit = glm(Direction ~ ., data=MyWeekly, family="binomial")

We can then summarise the fit of the model using the summary function:

summary(logreg_fit)

## 
## Call:
## glm(formula = Direction ~ ., family = "binomial", data = MyWeekly)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.7071  -1.2578   0.9941   1.0873   1.4665  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)  
## (Intercept) 17.225822  37.890522   0.455   0.6494  
## Year        -0.008500   0.018991  -0.448   0.6545  
## Lag1        -0.040688   0.026447  -1.538   0.1239  
## Lag2         0.059449   0.026970   2.204   0.0275 *
## Lag3        -0.015478   0.026703  -0.580   0.5622  
## Lag4        -0.027316   0.026485  -1.031   0.3024  
## Lag5        -0.014022   0.026409  -0.531   0.5955  
## Volume       0.003256   0.068836   0.047   0.9623  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1496.2  on 1088  degrees of freedom
## Residual deviance: 1486.2  on 1081  degrees of freedom
## AIC: 1502.2
## 
## Number of Fisher Scoring iterations: 4

Inspecting the \(p\)-value column (i.e. the Pr(>|z|) column), we see that only Lag2 has a coefficient which is significantly different from zero when testing at the 5% level. In other words, if we label Lag1, \(\ldots\), Lag5 as \(x_1, \ldots, x_5\) and Volume as \(x_6\) and then perform six hypothesis tests: \[\begin{equation*} H_0: \beta_j = 0 \quad \text{versus} \quad H_1: \beta_j \ne 0, \end{equation*}\] we would only reject the null hypothesis at the 5% level for \(j=2\), when testing the effect of Lag2. This suggests that for the other variables, given a model that already contains all the other predictors, the predictor in question adds very little in terms of forecasting whether the stock market is up or down.

We can use R to calculate the values that our fitted model would predict for the predictor variables on the 1st, \(\ldots\), \(n\)th rows of our matrix of predictor variables by: (i) using the predict function to get the predicted probabilities \(\hat{p}_1,\ldots,\hat{p}_n\) that the response is equal to 1 and then (ii) applying a classification rule to get the binary predictions \(\hat{y}_1,\ldots,\hat{y}_n\). As arguments to the predict function, we simply pass the object returned by the glm function, the data frame containing the predictor variables at which we want predictions and the argument type="response" which ensures the values returned are the predicted probabilities. In this case we have:

## Compute the fitted values: 
phat = predict(logreg_fit, MyWeekly, type="response")
yhat = as.numeric(ifelse(phat > 0.5, 1, 0))
## Print first few elements:
head(yhat)

## [1] 1 1 1 0 1 1

## Compare with actual values:
head(MyWeekly$Direction)

## [1] 0 0 1 1 1 0

As we will see in the lecture-workshops, training (and test) error for classification problems is generally measured as the proportion of misclassified observations, i.e. the proportion of observations where \(\hat{y}_i\) is not equal to \(y_i\). Calculate the training error for this model.
Please think about this yourself before uncovering the solution.

Click for solution

## Compute the fitted values: did this above and they are stored in yhat
## Compute training error:
(training_error = 1 - mean(yhat == MyWeekly$Direction))

## [1] 0.43618

We see that the training error is around 43.62%.

If we simply flipped a coin to decide whether to predict an increase or decrease, the training error would be 50%. It seems we are doing slightly better than this. However, the training error uses the same data to train and test the model and so gives an optimistic assessment of the performance of the classifier.

3.2 Best Subset Selection

In the Section 2 we saw that none of the predictors seem to have a particularly noticeable effect on the response. Moreover, in the previous section, we saw that the full model contains more predictors than it needs. This suggests we might be able to employ subset selection methods to produce a model with fewer than \(p\) predictors and better predictive performance. This is essentially because we are able to learn the effects of the reduced number of predictors more precisely and so our predictions over unseen data show less variability. In this module we only consider best subset selection where our comparison considers all \(2^p\) possible models (i.e. the model with no predictors, all \(p\) models with one predictor, all \(\binom{p}{2}\) models with two predictors, and so on). This method would be infeasible if \(p\) was too large, say larger than about 40, in which case there are other methods that use heuristics to find a “good” model without considering all possible models. These are studied in the context of linear regression in the Machine Learning module.

As remarked in lecture-workshops, we can perform best subset selection for generalised linear models, of which logistic regression is an example, using the bestglm function in the package of the same name. The algorithm is exactly the same as the one we studied for multiple linear regression except that when comparing models containing the same number of predictors, we use the negative loglikelihood, rather than the residual sum of squares. (Though, as an aside, in multiple linear regression, comparison based on the residual sum of squares is equivalent to comparison based on the negative loglikelihood in terms of the ranking it produces). When comparing the best-fitting models containing \(0, 1, \ldots, p\) predictors, i.e. the models we call \(\mathcal{M}_0, \mathcal{M}_1, \ldots, \mathcal{M}_p\), various model-comparison criteria can be used. Widely used examples are the AIC (equivalent to Mallow’s \(C_p\) in the context of multiple linear regression), the BIC and the cross-validation test error. In all three cases small values of the information criterion indicate a “better” model.

Before we start, load the bestglm package in R

## Load the bestglm package
library(bestglm)

then look at the help file for the bestglm function by typing ?bestglm in the console. You will see that the first argument is a data frame called Xy. Although it is not spelled out in the documentation, this means that the data must be arranged so that the last column of Xy is the response (i.e. y) variable and all the preceding columns are predictor (i.e. X) variables. If we check our data set:

head(MyWeekly)

##   Year   Lag1   Lag2   Lag3   Lag4   Lag5    Volume Direction
## 1 1990  0.816  1.572 -3.936 -0.229 -3.484 0.1549760         0
## 2 1990 -0.270  0.816  1.572 -3.936 -0.229 0.1485740         0
## 3 1990 -2.576 -0.270  0.816  1.572 -3.936 0.1598375         1
## 4 1990  3.514 -2.576 -0.270  0.816  1.572 0.1616300         1
## 5 1990  0.712  3.514 -2.576 -0.270  0.816 0.1537280         1
## 6 1990  1.178  0.712  3.514 -2.576 -0.270 0.1544440         0

we see that the final column is Direction which is our response variable. We can therefore pass the MyWeekly data frame as it is.

Create some made-up data in R: \(\phantom{X}\) mydata = data.frame(x1=rnorm(100), y=runif(100), x2=rnorm(100)).
In mydata, the columns labelled x1 and x2 are predictor variables and y is the binary response variable. Create a new matrix called mydata_2 in a suitable form to be passed to the bestglm function.
Please have a go by yourself before uncovering the solution.

Click for solution

## Enter made-up data:
mydata = data.frame(x1=rnorm(100), y=runif(100), x2=rnorm(100))
## Make the response variable the final column:
mydata_2 = mydata[, c(1, 3, 2)]
## Check it seems okay:
head(mydata_2)

##           x1         x2          y
## 1  0.2167549  0.8769847 0.75326554
## 2 -0.5424926 -0.8161958 0.79296577
## 3  0.8911446  1.5392933 0.45417758
## 4  0.5959806  1.3745257 0.36082207
## 5  1.6356180 -0.4832487 0.36074237
## 6  0.6892754  0.5503500 0.06116853

Returning to our stock market data, we can now apply best subset selection using the AIC and BIC by two applications of the bestglm function:

## Apply best subset selection
bss_fit_AIC = bestglm(MyWeekly, family=binomial, IC="AIC")
bss_fit_BIC = bestglm(MyWeekly, family=binomial, IC="BIC")

Note that, unlike the regsubsets function of the leaps package, each function call only gives the results based on one information criterion.

The object returned by the bestglm function contains a number of useful components. You can read about the components of the object by typing ?bestglm again in the console and reading the “Value” section. We will extract the component called Subsets which tells us which predictors are included in \(\mathcal{M}_0, \mathcal{M}_1, \ldots, \mathcal{M}_p\) and the value of the chosen information criterion for each of these models:

## Examine the results
bss_fit_AIC$Subsets

##    Intercept  Year  Lag1  Lag2  Lag3  Lag4  Lag5 Volume logLikelihood      AIC
## 0       TRUE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE     -748.1012 1496.202
## 1       TRUE FALSE FALSE  TRUE FALSE FALSE FALSE  FALSE     -745.2093 1492.419
## 2*      TRUE FALSE  TRUE  TRUE FALSE FALSE FALSE  FALSE     -744.1102 1492.220
## 3       TRUE FALSE  TRUE  TRUE FALSE  TRUE FALSE  FALSE     -743.6727 1493.345
## 4       TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  FALSE     -743.4081 1494.816
## 5       TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  FALSE     -743.2229 1496.446
## 6       TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  FALSE     -743.0794 1498.159
## 7       TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE   TRUE     -743.0783 1500.157

bss_fit_BIC$Subsets

##    Intercept  Year  Lag1  Lag2  Lag3  Lag4  Lag5 Volume logLikelihood      BIC
## 0*      TRUE FALSE FALSE FALSE FALSE FALSE FALSE  FALSE     -748.1012 1496.202
## 1       TRUE FALSE FALSE  TRUE FALSE FALSE FALSE  FALSE     -745.2093 1497.412
## 2       TRUE FALSE  TRUE  TRUE FALSE FALSE FALSE  FALSE     -744.1102 1502.206
## 3       TRUE FALSE  TRUE  TRUE FALSE  TRUE FALSE  FALSE     -743.6727 1508.325
## 4       TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  FALSE     -743.4081 1514.788
## 5       TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  FALSE     -743.2229 1521.411
## 6       TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  FALSE     -743.0794 1528.117
## 7       TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE   TRUE     -743.0783 1535.108

By construction, the implied models \(\mathcal{M}_0, \mathcal{M}_1, \ldots, \mathcal{M}_p\) are the same in each case; all that differs is the final column giving the information criterion. The models minimising the AIC and BIC are starred in each case. They can also be extracted from the bss_fit_AIC and bss_fit_BIC objects:

## Identify best-fitting models
(best_AIC = bss_fit_AIC$ModelReport$Bestk)

## [1] 2

(best_BIC = bss_fit_BIC$ModelReport$Bestk)

## [1] 0

It seems that models with 0 or 2 predictors are to be preferred. However, we defer making our overall choice until we have considered a third model comparison criterion: the \(k\)-fold cross-validation error. Before we apply \(k\)-fold cross-validation in this context, we will introduction the general idea of \(k\)-fold cross-validation for classification methods.

3.3 \(k\)-fold Cross-Validation

As in the case of multiple linear regression, we can estimate the test error for a classifier based on logistic regression by using \(k\)-fold cross-validation. In this lab, we will consider 10-fold cross-validation. To this end, as previously, we begin by dividing the data into 10 folds of approximately equal size:

## Set the seed (say, at 5) to make the analysis reproducible
set.seed(5)
## Sample the fold-assignment index
nfolds = 10
fold_index = sample(nfolds, n, replace=TRUE)
## Print the first few fold-assignments
head(fold_index)

## [1] 2 9 9 9 5 7

So observation 1 is assigned to fold 2, observation 2 is assigned to fold 9, and so on.

Referring to the worksheet from last week, write a function called logistic_reg_fold_error based on the reg_fold_error function. It should calculate the test error given a matrix of predictor variables X, a vector of response variables y and a vector of booleans test_data whose \(i\)th element is equal to TRUE if observation \(i\) is in the test set and equal to FALSE if observation \(i\) is in the training set. Note:
- You will need to change the line that fits the model to the training data
- You will need to change the line that generates the predictions (i.e. yhat) over the test data
- You will need to change the line that calculates the test error so it uses the misclassification rate and not the mean-squared error.
Please have a go by yourself before uncovering the solution.

Click for solution

logistic_reg_fold_error = function(X, y, test_data) {
  Xy = data.frame(X, y=y)
  if(ncol(Xy)>1) tmp_fit = glm(y ~ ., data=Xy[!test_data,], family="binomial")
  else tmp_fit = glm(y ~ 1, data=Xy[!test_data,,drop=FALSE], family="binomial")
  phat = predict(tmp_fit, Xy[test_data,,drop=FALSE], type="response")
  yhat = ifelse(phat > 0.5, 1, 0) 
  yobs = y[test_data]
  test_error = 1 - mean(yobs == yhat)
  return(test_error)
}

For the set of predictor variables passed through X and the binary response passed through y, the logistic_reg_fold_error function can be used to calculate the test error given a particular split of the data into training and validation sets.

Referring to the worksheet from last week, recall our function general_cv. For convenience, it is reproduced below:

general_cv = function(X, y, fold_ind, fold_error_function) {
  p = ncol(X)
  Xy = cbind(X, y=y)
  nfolds = max(fold_ind)
  if(!all.equal(sort(unique(fold_ind)), 1:nfolds)) stop("Invalid fold partition.")
  fold_errors = numeric(nfolds)
  # Compute the test error for each fold
  for(fold in 1:nfolds) {
    fold_errors[fold] = fold_error_function(X, y, fold_ind==fold)
  }
  # Find the fold sizes
  fold_sizes = numeric(nfolds)
  for(fold in 1:nfolds) fold_sizes[fold] = length(which(fold_ind==fold))
  # Compute the average test error across folds
  test_error = weighted.mean(fold_errors, w=fold_sizes)
  # Return the test error
  return(test_error)
}

For any simple regression or classification method, we can use this general function to calculate the cross-validation error by passing a function fold_error_function which tailors it to the specific regression or classification method we are interested in. More specifically, this function fold_error_function should calculate the test error for a particular split of the data into test and validation data. It should take as arguments a matrix of predictors X, a response variable y and a vector of booleans fold_ind which is equal to TRUE in position \(i\) if the \(i\)th observation is in the validation set and equal to FALSE otherwise. The function logistic_reg_fold_error that we wrote above meets this requirements for logistic regression. We can therefore use the function general_cv with logistic_reg_fold_error to calculate the test error of our full model as follows:

(test_error = general_cv(MyWeekly[,1:p], MyWeekly[,p+1], fold_index, logistic_reg_fold_error))

## [1] 0.4536272

Not surprisingly, we see that the test error is larger than the training error, though still slightly better than flipping a coin. Hopefully it comes as no surprise that this simple method cannot accurately predict changes in the stock market!

Now that we have seen how \(k\)-fold cross-validation works in general, we can apply it as another criteria for picking the number of predictors in best subset selection.

3.4 Using \(k\)-fold Cross-Validation in Best Subset Selection

We shall write a function which estimates the test error for best fitting models with \(0, 1, \ldots, p\) predictors using 10-fold cross-validation.

A function which wraps around logistic_reg_fold_error to calculate the test error for best-fitting models with \(0, 1, \ldots, p\) predictors is given below:

logistic_reg_bss_cv = function(X, y, fold_ind) {
  p = ncol(X)
  Xy = data.frame(X, y=y)
  X = as.matrix(X)
  nfolds = max(fold_ind)
  if(!all.equal(sort(unique(fold_ind)), 1:nfolds)) stop("Invalid fold partition.")
  fold_errors = matrix(NA, nfolds, p+1) # p+1 because M_0 included in the comparison
  for(fold in 1:nfolds) {
    # Using all *but* the fold as training data, find the best-fitting models 
    # with 0, 1, ..., p predictors, i.e. identify the predictors in M_0, M_1, ..., M_p
    tmp_fit = bestglm(Xy[fold_ind!=fold,], family=binomial, IC="AIC")
    best_models = as.matrix(tmp_fit$Subsets[,2:(1+p)])
    # Using the fold as test data, find the test error associated with each of 
    # M_0, M_1,..., M_p
    for(k in 1:(p+1)) {
      fold_errors[fold, k] = logistic_reg_fold_error(X[,best_models[k,]], y, fold_ind==fold)
    }
  }
  # Find the fold sizes
  fold_sizes = numeric(nfolds)
  for(fold in 1:nfolds) fold_sizes[fold] = length(which(fold_ind==fold))
  # For models with 0, 1, ..., p predictors compute the average test error across folds
  test_errors = numeric(p+1)
  for(k in 1:(p+1)) {
    test_errors[k] = weighted.mean(fold_errors[,k], w=fold_sizes)
  }
  # Return the test error for models with 0, 1, ..., p predictors
  return(test_errors)
}

Let us talk through how the function works, assuming there are 10 folds, i.e. nfolds=10. We focus first on the first for loop over the fold variable. When fold 1 is taken as the validation data, we can use folds 2–10 as training data and apply the bestglm function to find the subset of predictors in the best-fitting models with \(0, 1, \ldots, p\) predictors. Passing the predictors in the best-fitting model with \(k\) predictors, we can then apply our function logistic_reg_fold_error to fit this \(k\)-predictor model to our training data (folds 2–10) and compute the test error over our validation data (fold 1). We perform this step \(p+1\) times – once for each number of predictors, \(k=0,1,\ldots,p\). Finally we repeat this whole procedure, taking fold 2 as the validation data and folds 1 and 3–10 as training data. We then repeat again taking fold 3 as the validation data and folds 1–2 and 4–10 as training data. And so on. For every value of \(k=0,1,\ldots,p\), we then have the test error associated with each of the 10 folds for the model with \(k\) predictors. In the for loop over k towards the end of the function, these 10 values are averaged to get the test error for the model with \(k\) predictors. So we end up with the test error for models with \(0, 1, \ldots, p\) predictors calculated by 10-fold cross validation.

We can now apply our function to the stock market data:

## Apply the cross-validation for best subset selection function
cv_errors = logistic_reg_bss_cv(MyWeekly[,1:p], MyWeekly[,p+1], fold_index)
## Identify the number of predictors in the model which minimises test error
(best_cv = which.min(cv_errors) - 1)

## [1] 1

where we add one to the output of the which.min function because the test error for model with 0 predictors has index 1. Cross-validation suggests the model with 1 predictors. Referring back to Section 3.2, AIC and BIC suggested the models with 2 and 0 predictors, respectively. As for multiple linear regression, different criteria often suggest different models are “best”, and this is the case here. In order to reconcile the differences and choose a single “best” model we can generate a plot to show how the criteria vary with the number of predictors:

## Create multi-panel plotting device
par(mfrow=c(2, 2))
## Produce plots, highlighting optimal value of k
plot(0:p, bss_fit_AIC$Subsets$AIC, xlab="Number of predictors", ylab="AIC", type="b")
points(best_AIC, bss_fit_AIC$Subsets$AIC[best_AIC+1], col="red", pch=16)
plot(0:p, bss_fit_BIC$Subsets$BIC, xlab="Number of predictors", ylab="BIC", type="b")
points(best_BIC, bss_fit_BIC$Subsets$BIC[best_BIC+1], col="red", pch=16)
plot(0:p, cv_errors, xlab="Number of predictors", ylab="CV error", type="b")
points(best_cv, cv_errors[best_cv+1], col="red", pch=16)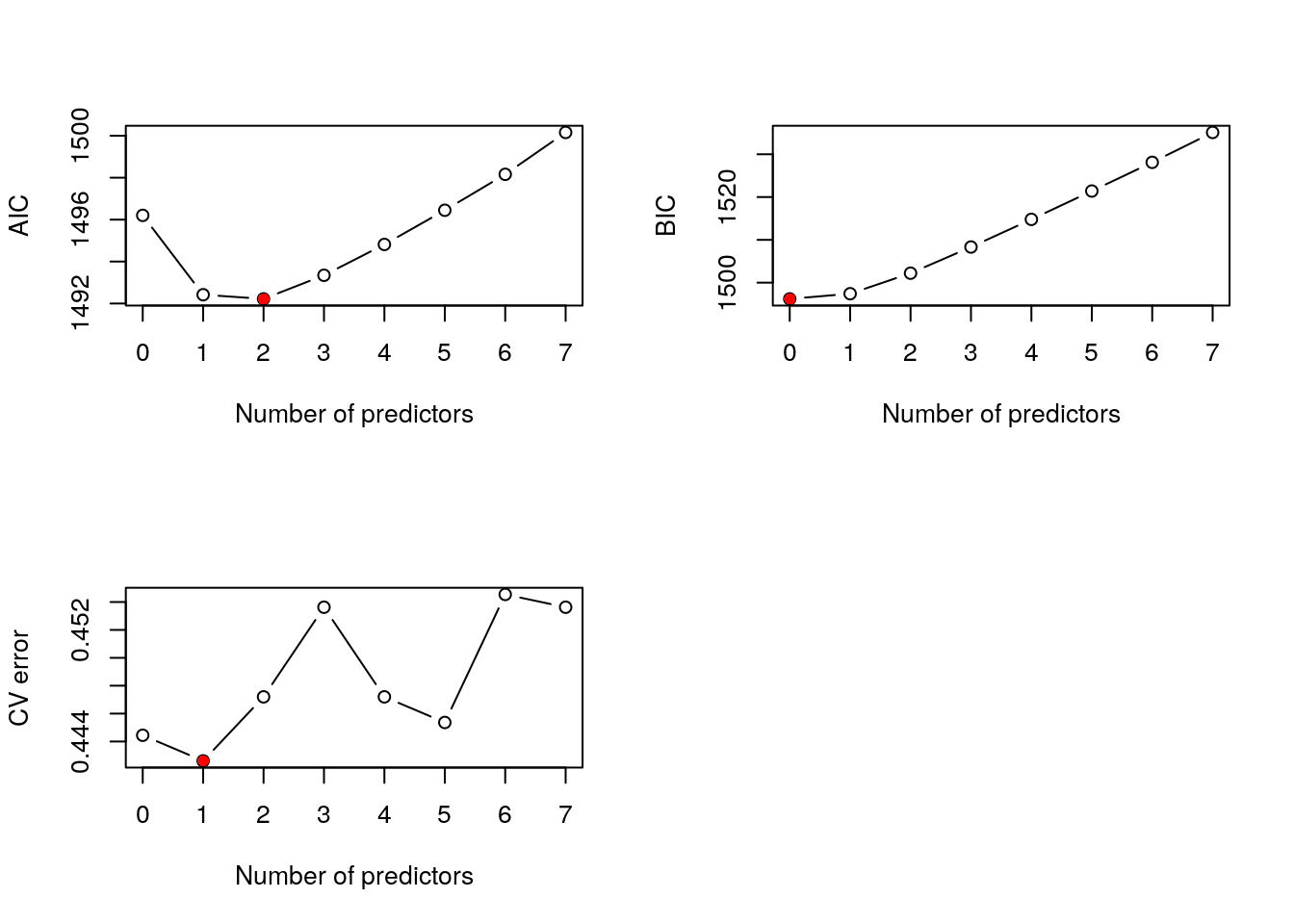

Figure 3.1: Best subset selection for the Weekly data.

This generates the plots above. It seems like the model with one predictor is a good compromise. We can extract the variables from the best-fitting 1-predictor model from the output of the bestglm function:

pstar = 1
## Check which predictors are in the 2-predictor model
bss_fit_AIC$Subsets[pstar+1,]

##    Intercept  Year  Lag1 Lag2  Lag3  Lag4  Lag5 Volume logLikelihood      AIC
## 1       TRUE FALSE FALSE TRUE FALSE FALSE FALSE  FALSE     -745.2093 1492.419

## Construct a reduced data set containing only the 2 selected predictors
bss_fit_AIC$Subsets[pstar+1, 2:(p+1)]

##     Year  Lag1 Lag2  Lag3  Lag4  Lag5 Volume
## 1  FALSE FALSE TRUE FALSE FALSE FALSE  FALSE

(indices = which(bss_fit_AIC$Subsets[pstar+1, 2:(p+1)]==TRUE))

## [1] 3

MyWeekly_red = MyWeekly[,c(indices, p+1)]
## Obtain regression coefficients for this model
logreg1_fit = glm(Direction ~ ., data=MyWeekly_red, family="binomial")
summary(logreg1_fit)

## 
## Call:
## glm(formula = Direction ~ ., family = "binomial", data = MyWeekly_red)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -1.564  -1.267   1.008   1.086   1.386  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  0.21473    0.06123   3.507 0.000453 ***
## Lag2         0.06279    0.02636   2.382 0.017230 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1496.2  on 1088  degrees of freedom
## Residual deviance: 1490.4  on 1087  degrees of freedom
## AIC: 1494.4
## 
## Number of Fisher Scoring iterations: 4

We see that the selected model uses Lag2 as a predictor and its coefficient in the 1-predictor model is significantly different from zero. The corresponding coefficient is 0.06279. This is positive which suggests that higher returns two weeks ago are associated with a higher probability of a positive return today.

What is the test error associated with our chosen 1-predictor model? You might think you can extract it from the cv_errors vector calculated above. However, this would simply give us an estimate of the test error for a 1-predictor model. Since the bestglm function in logistic_reg_bss_cv might have picked a different 1-predictor model \(\mathcal{M}_1\) for each of the 10 training sets (i.e. folds 2–10, folds 1 and 3–10, \(\ldots\), folds 1–9), we have not necessarily estimated the test error associated with our 1-predictor model, i.e. the model with predictors Lag1 and Lag2.

We can therefore estimate the test error of our 1-predictor model as follows:

(test_error = general_cv(MyWeekly_red[,1:pstar], MyWeekly_red[,pstar+1], fold_index, logistic_reg_fold_error))

## [1] 0.4426079

We see that the test error is slightly lower than that we obtained for the full-model.

4 Linear Discriminant Analysis

Continuing to use only Lag2 as a predictor, now we will use the full data set to build our Bayes classifier for LDA:

## Load the MASS package:
library(MASS)
## Apply LDA:
(lda_fit = lda(Direction ~ ., data=MyWeekly_red))

## Call:
## lda(Direction ~ ., data = MyWeekly_red)
## 
## Prior probabilities of groups:
##         0         1 
## 0.4444444 0.5555556 
## 
## Group means:
##          Lag2
## 0 -0.04042355
## 1  0.30428099
## 
## Coefficients of linear discriminants:
##            LD1
## Lag2 0.4251523

We see that when Direction=0 (i.e. when the stock market goes down), the means of the predictor Lag2 is -0.0404236. When Direction=1 (i.e. when the stock market goes up), the mean is 0.304281. Notice that since we can regard our data as a random sample of (consecutive) weekly stock returns, we can estimate the prior membership probabilities \(\pi_1\) and \(\pi_2\) using the default sample proportions displayed in the output above.

Referring to the associated lecture-workshop notes if necessary, write a few lines of code to compute the (training) confusion matrix and training error.
Please have a go by yourself before uncovering the solution.

Click for solution

## Compute predicted values:
lda_predict = predict(lda_fit, MyWeekly_red)
yhat = lda_predict$class
## Calculate confusion matrix:
(confusion = table(Observed=MyWeekly_red$Direction, Predicted=yhat))

##         Predicted
## Observed   0   1
##        0  33 451
##        1  25 580

## Calculate training error:
1 - mean(MyWeekly_red$Direction == yhat)

## [1] 0.4370983

We shall use 10-fold cross-validation again to estimate the test error.

Modify the function logistic_reg_fold_error we wrote for logistic regression so that it calculates the test error for LDA given a particular split of the data into training and validation data. Note that we need only consider the case where ncol(Xy)>1 since discriminant analysis does not really make sense if there are no predictors.
Please have a go by yourself before uncovering the solution.

Click for solution

lda_fold_error = function(X, y, test_data) {
  Xy = data.frame(X, y=y)
  if(ncol(Xy)>1) tmp_fit = lda(y ~ ., data=Xy[!test_data,])
  tmp_predict = predict(tmp_fit, Xy[test_data,])
  yhat = tmp_predict$class 
  yobs = y[test_data]
  test_error = 1 - mean(yobs == yhat)
  return(test_error)
}

We can now pass this function as an argument to the general_cv function to compute the test error by cross-validation. To keep the comparison with logistic regression fair, we will use the same partition of the data into folds, i.e. the same fold_index vector:

(test_error = general_cv(MyWeekly_red[,1:pstar], MyWeekly_red[,pstar+1], fold_index, lda_fold_error))

## [1] 0.4444444

We note that our test error is almost identical to that obtained using the 1-predictor logistic regression model.

5 Quadratic discriminant analysis

By making minor modifications to the code for LDA above, calculate the training error for the Bayes classifier for QDA. Similarly, calculate the tests error using 10-fold cross-validation and the same partition of the data into folds.
Please have a go by yourself before uncovering the solution.

Click for solution

First we calculate the training error:

## Apply QDA:
(qda_fit = qda(Direction ~ ., data=MyWeekly_red))

## Call:
## qda(Direction ~ ., data = MyWeekly_red)
## 
## Prior probabilities of groups:
##         0         1 
## 0.4444444 0.5555556 
## 
## Group means:
##          Lag2
## 0 -0.04042355
## 1  0.30428099

## Compute predicted values:
qda_predict = predict(qda_fit, MyWeekly_red)
yhat = qda_predict$class
## Calculate confusion matrix:
(confusion = table(Observed=MyWeekly_red$Direction, Predicted=yhat))

##         Predicted
## Observed   0   1
##        0   0 484
##        1   0 605

## Calculate training error:
1 - mean(MyWeekly_red$Direction == yhat)

## [1] 0.4444444

Now we modify slightly the lda_fold_error function to use QDA instead of LDA:

qda_fold_error = function(X, y, test_data) {
  Xy = data.frame(X, y=y)
  if(ncol(Xy)>1) tmp_fit = qda(y ~ ., data=Xy[!test_data,])
  tmp_predict = predict(tmp_fit, Xy[test_data,])
  yhat = tmp_predict$class 
  yobs = y[test_data]
  test_error = 1 - mean(yobs == yhat)
  return(test_error)
}

Finally, we apply the general_cv function to calculate the test error:

(test_error = general_cv(MyWeekly_red[,1:pstar], MyWeekly_red[,pstar+1], fold_index, qda_fold_error))

## [1] 0.4471993

It seems the performance of QDA is slightly worse than that for LDA and logistic regression in this example.

The general function general_cv does not return the test confusion matrix because it would not be meaninfully defined for regression problems. How might you write a new function, just for classification problems, that can do this?

Click for solution

I would like you to have a think about this for yourselves but please do ask if you don’t know where to start.

Labs on Classification Methods

Sarah Heaps

1 Background

2 Exploratory Data Analysis

3 Logistic Regression

3.1 The Full Model

3.2 Best Subset Selection

3.3 \(k\)-fold Cross-Validation

3.4 Using \(k\)-fold Cross-Validation in Best Subset Selection

4 Linear Discriminant Analysis

5 Quadratic discriminant analysis