Classification Methods
Sarah Heaps
Download Lecture-Workshop Notes for Week 4
1 Introduction
1.1 Key Ideas
Suppose that individuals (or items) can be divided into \(K \ge 2\) groups that can, in principle, be observed, e.g. patients with and without a particular disease. Suppose further that we can take measurements on \(p\) variables for each individual. Given a \(p\)-variate observation on an individual whose group membership is unknown, the general objective of classification is to assign that individual to a group.
Equivalently, for a collection of individuals (or items) suppose that we can take measurements on \(p+1\) variables, the last of which is categorical and indicates group membership. Then classification can be regarded as the problem of predicting the value of the categorical variable given the values of the \(p\) others. In this framework we would call the categorical variable our response variable and the other \(p\) variables the predictor or explanatory variables.
Typically, in classification problems we use a set of “labelled” data (i.e. data where group membership is known) to construct a rule for classifying an “unlabelled” observation (i.e. an observation whose group membership is unknown). Classification can therefore be regarded as a type of supervised learning because labelled observations are available to learn about the relationship between observations and group membership. (In the module “Data Exploration, Visualization, and Unsupervised Learning” you will learn about a related method – cluster analysis – in which labelled observations are not available). Therefore, like in multiple linear regression, classification methods (or “classifiers”) are often assessed on the basis of their predictive performance using techniques such as cross-validation; see Section 5.
1.2 Motivating Example - Banknote Authentication Data
These data were extracted from 1372 images taken from genuine and forged banknotes. The images were digitised into \(400 \times 400\) arrays of pixels and then summarised into four continuously valued summary statistics. For each banknote, the data set records whether the banknote was genuine or forged, along with the four numerical summaries of the image.
Thus, if we were to arrange these data into a \(n \times p\) array, we would have
- \(n=1372\) rows corresponding to the images;
- \(p=5\) columns corresponding to the variables: the label (genuine / forgery) and the 4 numerical summaries.
As there are two possible values for the label for each banknote, \(K=2\) here. In this example the purpose of collecting the data was to “train” a classification method to automatically categorise new banknotes whose status (forged or genuine) was not yet known, using information extracted from a digitized image. We shall return to this example in Section 5.3.3.
2 Model-Based Classification
2.1 Introduction
In the introduction above we considered two ways of thinking about the classification problem: (i) as a means of partitioning multivariate observations into groups; and (ii) as a means of predicting a categorical response using a collection of predictor variables. The first framework naturally motivates a discriminant-based approach to classification whilst the second motivates a regression-based approach. We begin this chapter with a brief discussion of both approaches to demonstrate how they are related.
For each individual / item we will assume we can observe values for \(Y\) – a categorical random variable that can take one of \(K\) possible values – and \(X_1,\ldots,X_p\) – \(p\) (random) variables which we will assume, for now, are continuous. We focus exclusively on model-based approaches to classification in which our goal will be to come up with a method for computing \[\begin{equation*} \Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p) \end{equation*}\] for each possible value, \(k = 1,\ldots, K\), where clearly \(\sum_{k=1}^K \Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p) = 1\). In words, this is
“What is the probability that \(Y\) takes the value \(k\) for an individual / item where \(X_1\) takes the value \(x_1\), \(X_2\) takes the value \(x_2\), and so on up to \(X_p\) taking the value \(x_p\)”?
For example, for a collection of patients presenting with a particular complaint, if \(Y\) represents whether the patient has a particular disease and \(X_1, \ldots, X_p\) represents a set of clinical measurements taken on the patient, we would want to be able to answer the question
“What is the probability that an individual has the disease if they have clinical measurements of \(x_1,\ldots,x_p\)?”
As such, \(Y\) is often regarded as a response variable and \(X_1,\ldots,X_p\) as a collection of (random) predictor variables.
2.2 Regression-Based Approaches
The most direct way of specifying the probabilities \(\Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p)\) is by constructing a probability model for \(Y\) conditional on \(X_i\) taking the value \(x_i\) for \(i=1,\ldots,p\). If \(Y\) could be treated as a continuous variable, we could construct this kind of probability model by using multiple linear regression, assuming a normal distribution for the error terms. This is equivalent to adopting the model \[\begin{equation} Y | X_1 = x_1, \ldots, X_p = x_p \sim \mathrm{N}(\mu, \sigma^2)\tag{2.1} \end{equation}\] where the mean \(\mu\) depends on the predictor variables \(x_1,\ldots,x_p\) through \[\begin{equation*} \mu = \beta_0 + \beta_1 x_{1} + \ldots + \beta_p x_{p}. \end{equation*}\]
However the assumption of a normal distribution in (2.1) will clearly not be appropriate if \(Y\) is categorical. Suppose, for simplicity that \(K=2\) so that \(Y\) admits two possible values, normally labelled as 0 and 1 (we say that \(Y\) is binary). In this case, a suitable model for \(Y\) is the Bernoulli distribution. This is a special case of the Binomial distribution that you studied in “Introduction to Mathematics for Data Science (IMDS)”. A Bernoulli random variable \(Y\) takes two possible values – 0 and 1 – and its distribution depends on a single parameter, \(\mu\), called the probability of success, which is a real number that lies between 0 and 1. If \(Y\) has a Bernoulli distribution with probability of success \(\mu\), which we write \(Y \sim \mathrm{Bern}(\mu)\), then it has probability mass function \[\begin{equation*} \Pr(Y = 0) = 1 - \mu \quad \text{and} \quad \Pr(Y = 1) = \mu. \end{equation*}\] The mean \(E(Y)\) of the distribution is defined by \[\begin{equation*} E(Y) = \sum_{y=0}^1 y \Pr(Y = y) = \Pr(Y = 1) = \mu. \end{equation*}\]
Therefore, if our response variable \(Y\) is binary, we might simply replace (2.1) with
\[\begin{equation*}
Y | X_1 = x_1, \ldots, X_p = x_p \sim \mathrm{Bern}(\mu)
\end{equation*}\]
and model the mean \(E(Y)=\mu\) as per linear regression where it is expressed as a linear combination of the predictor variables, called the linear predictor. In other words, denoting the linear predictor by \(\eta\) we could write
\[\begin{equation*}
\eta = \beta_0 + \beta_1 x_{1} + \ldots + \beta_p x_{p}
\end{equation*}\]
and take \(\mu = \eta\). However, this still isn’t right because the linear predictor \(\eta\) can take any real value and the mean \(\mu\) of a Bernoulli random variable is a probability which must lie between 0 and 1. So as a final modification, instead of modelling \(\mu = \eta\), we instead take
\[\begin{equation*}
g(\mu) = \eta
\end{equation*}\]
where \(g\) is a function – called a link function – which maps \(\mu\) (which lies between 0 and 1) to a value in the space of values that the linear predictor can take (i.e. all real numbers). If we take \(g(\mu) = \log \{ \mu / (1 - \mu) \}\), we get logistic regression. If we take \(g(\mu) = \Phi^{-1}(\mu)\), where \(\Phi(\cdot)\) is the standard normal cumulative distribution function (pnorm in R) and \(\Phi^{-1}(\cdot)\) its inverse (qnorm in R), we get probit regression. There are then simple generalisations, e.g. multinomial logistic regression, which extend this approach to the case where the categorical variable has \(K>2\) possible values. We consider logistic regression in more detail in Section 3.
Regression models like these are examples of generalised linear models which generalise the linear model to allow the response variable to have a non-normal distribution. All we need to do to get another model from this class is choose a different distribution for \(Y | X_1 = x_1, \ldots, X_p = x_p\) and then choose an appropriate link function to connect the mean of the distribution to the linear predictor. These types of model will be explored further in the module “Multilevel Modelling”.
2.3 Discriminant-Based Approaches
Although this regression approach is conceptually appealing, there is another, less direct, way of defining the conditional probabilities \(\Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p)\) for each value \(k = 1,\ldots,K\). This involves formulating the model the “other way around” and defining conditional distributions for \((X_1 = x_1, \ldots, X_p = x_p | Y = k)\) for each \(k=1,\ldots,K\). This is easiest to understand in the context of an example. Suppose that \(Y\) represents whether a patient has a particular disease whilst \(X_1, \ldots, X_p\) represents a set of clinical measurements, such as blood pressure and body-mass-index, taken on that patient. Then we would need to construct a probability model for these clinical measurements conditional on a patient having the disease and another conditional on a patient not having the disease. In our model where we are conditioning on the patient having the disease, high values of blood pressure and body-mass-index might be quite likely. In our model where we are conditioning on the patient not having the disease, high values for these variables might be quite unlikely.
Now, for the purposes of illustration, let us suppose that the random variables in \(X_1, \ldots, X_p\) are all discrete-valued. Taking a discriminant-based approach, we would define a conditional probability mass function \[\begin{equation*} \Pr(X_1 = x_1, X_2 = x_2, \ldots, X_p = x_p | Y = k) \end{equation*}\] for each \(k=1,\ldots,K\), which would tell us the probability of observing \(X_i\) taking the value \(x_i\) for \(i=1,\ldots,p\) if we know \(Y=k\). Recall from the module “IMDS” that Bayes Theorem gives us a rule for “turning around” conditional probabilities. Applying it here gives \[\begin{equation} \Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p) = \frac{\Pr(X_1 = x_1, \ldots, X_p = x_p | Y = k) \Pr(Y = k)}{\sum_{\ell=1}^K \Pr(X_1 = x_1, \ldots, X_p = x_p | Y = \ell) \Pr(Y = \ell)}\tag{2.2} \end{equation}\] for each value \(k = 1,\ldots,K\). This is a type of Bayes classification and, in this context, \(\Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p)\) is the posterior probability that the categorical variable takes the value \(k\) or, equivalently, that the individual / item belongs to the \(k\)-th group. We denote this by \(p_k(x_1, \ldots, x_p)\). Note that to use a classification method based on this idea, we need to know the prior group membership probabilities, \(\Pr(Y = k) = \pi_k\) where \(\sum_{k=1}^K \pi_k = 1\). With this notation, we can express (2.2) more concisely as \[\begin{equation} p_k(x_1, \ldots, x_p) = \frac{\Pr(X_1 = x_1, \ldots, X_p = x_p | Y = k) \pi_k}{\sum_{\ell=1}^K \Pr(X_1 = x_1, \ldots, X_p = x_p | Y = k) \pi_{\ell}}.\tag{2.3} \end{equation}\]
If the random variables in \(X_1, \ldots, X_p\) are continuous-valued, rather than discrete-valued, there is an equivalent rule which gives us the posterior probabilities that we need, namely \[\begin{equation} p_k(x_1,\ldots,x_p) = \frac{f_k(x_1,\ldots,x_p) \pi_k}{\sum_{\ell=1}^K f_{\ell}(x_1,\ldots,x_p) \pi_{\ell}}\tag{2.4} \end{equation}\] for each value \(k = 1,\ldots,K\). Recall that when we have continuous random variables, we cannot use probability mass functions to specify their distribution because the probability that a continuous random variable takes any particular value is zero. Instead, we use probability density functions which indicate, in relative terms, which values are more or less likely. So to get (2.4) we have simply replaced each conditional probability mass function \(\Pr(X_1 = x_1, \ldots, X_p = x_p | Y = k)\) in (2.3) with a conditional probability density function denoted by \(f_k(x_1,\ldots,x_p)\).
Classification based on the conditional distribution of predictor variables given a categorical response, \((X_1 = x_1, \ldots, X_p = x_p | Y = k)\), is normally referred to as discriminant function analysis. In Section 4 we consider a special case in which the distribution of \((X_1, \ldots, X_p)\), conditional on \(Y = k\), is assumed to be a multivariate generalisation of the normal distribution called the multivariate normal distribution. The resulting methods are called linear discriminant analysis or quadratic discriminant analysis depending on assumptions we make about the variance parameter of the multivariate normal distribution.
3 Logistic Regression
3.1 The Model
Suppose that we have just two groups, \(K=2\), and that our categorical variable \(Y\) is labelled so that its two possible values are \(Y=0\) and \(Y=1\). Logistic regression was introduced in Section 2.2 as a means of directly specifying the probability \(\Pr(Y = 1 | X_1 = x_1, \ldots, X_p = x_p)\) (and hence, indirectly, \(\Pr(Y = 0 | X_1 = x_1, \ldots, X_p = x_p) = 1 - \Pr(Y = 1 | X_1 = x_1, \ldots, X_p = x_p)\)) using regression techniques. Specifically, we construct the linear predictor \[\begin{equation*} \eta = \beta_0 + \beta_1 x_{1} + \ldots + \beta_p x_{p}, \end{equation*}\] where \(\eta\) can take any real value, and assume that \[\begin{equation*} Y | X_1 = x_1, \ldots, X_p = x_p \sim \mathrm{Bern}(\mu), \end{equation*}\] where \(\mu = \Pr(Y = 1 | X_1 = x_1, \ldots, X_p = x_p)\) lies between 0 and 1. We then reconcile the difference between the values which can be taken by \(\mu\) and \(\eta\) by relating the mean \(\mu\) to the linear predictor \(\eta\) through a link function \(g\) where \(\eta = g(\mu)\). For logistic regression we use the logit-link \[\begin{equation*} \eta = \log\left( \frac{\mu}{1 - \mu} \right) \end{equation*}\] which has this name because the expression on the right-hand-side is called the logit function of \(\mu\). Using rules of algebra, it is possible to invert the above equation so that we get an expression for \(\mu\) in terms of \(\eta\) (instead of an expression for \(\eta\) in terms of \(\mu\)). This gives \[\begin{equation*} \mu = \frac{e^{\eta}}{1 + e^{\eta}} \end{equation*}\] in which the function on the right-hand-side is called the expit function (also known as the logistic function) of \(\eta\).
In other words, we model \[\begin{equation*} \mu = \Pr(Y = 1 | X_1 = x_1, \ldots, X_p = x_p) = \frac{\exp(\beta_0 + \beta_1 x_{1} + \ldots + \beta_p x_{p})}{1 + \exp(\beta_0 + \beta_1 x_{1} + \ldots + \beta_p x_{p})}. \end{equation*}\] For example, if \(p=1\) so that we have a single predictor variable, \(X_1 = X\), then our model for the mean reduces to \[\begin{equation*} \mu = \Pr(Y = 1 | X = x) = \frac{e^{\beta_0 + \beta_1 x}}{1 + e^{\beta_0 + \beta_1 x}}. \end{equation*}\] For this simple case, a plot of \(\mu\) against \(x\) is shown in Figure 3.1 for various values of \(\beta_0\) and \(\beta_1\).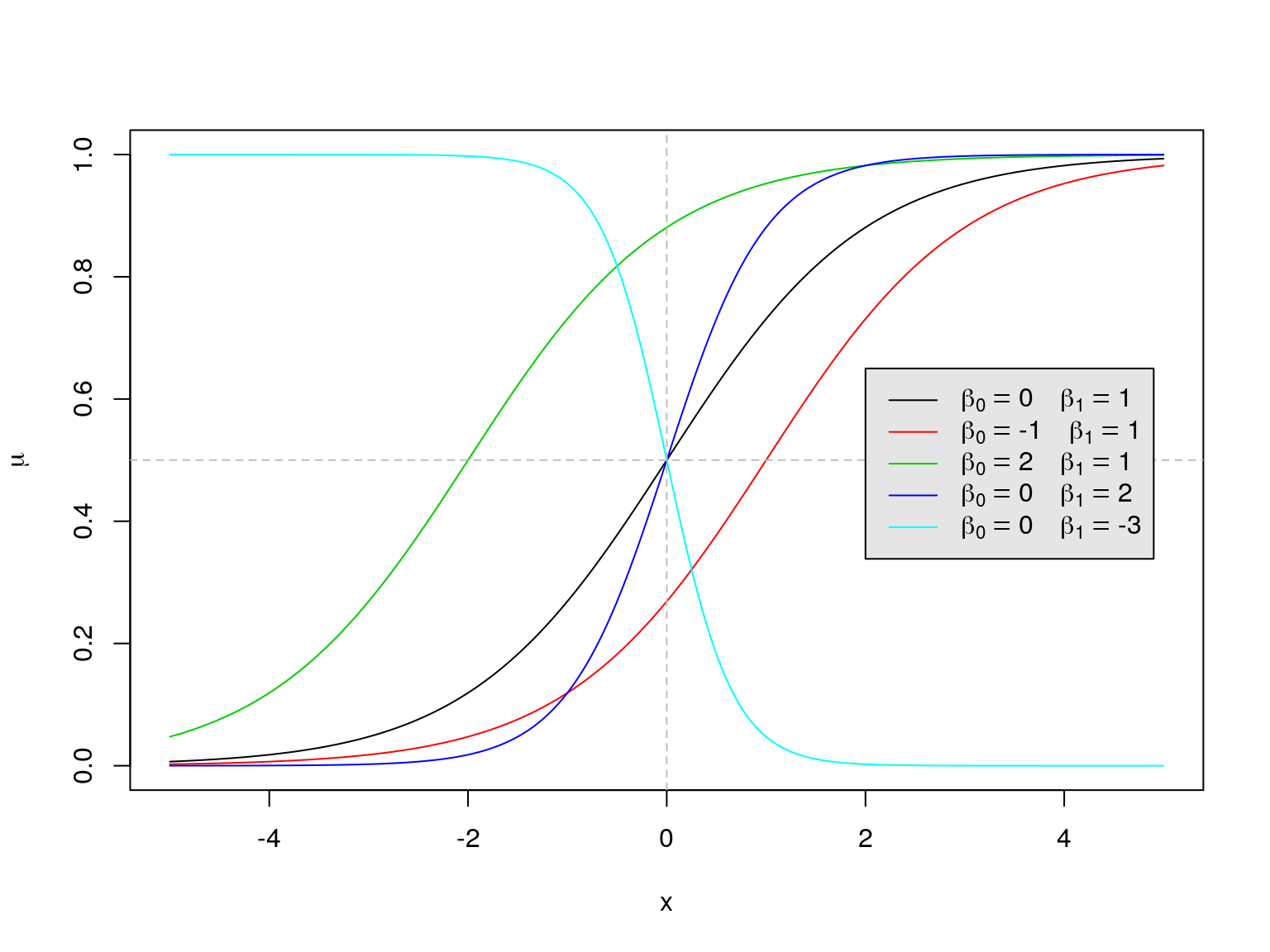
Figure 3.1: A plot of the logistic function \(e^{\beta_0 + \beta_1 x} / (1 + e^{\beta_0 + \beta_1 x})\) against \(x\) for various values of \(\beta_0\) and \(\beta_1\).
Notice that for each set of regression coefficients \(\beta_0\) and \(\beta_1\), we get an \(S\)-shaped curve which maps a real number \(x\) to a probability \(\mu\) that lies between 0 and 1. It can be shown that
- \(\beta_0\) affects the intercept, i.e. the point at which the curve cuts through the \(y\)-axis;
- \(\beta_1\) affects the “direction” of the curve and how quickly it flattens out in each tail:
- If \(\beta_1 > 0\) the curve slopes upwards from left to right; if \(\beta_1 < 0\) the curve slopes downwards from left to right; if \(\beta_1=0\) the curve is a straight horizontal line.
- The larger the value of \(\beta_1\) (ignoring its sign), the more quickly the curve flattens out in each tail, and hence the smaller the range of values of \(x\) over which the curve is notably different from 0 or 1.
This means that if \(\beta_1\) is positive, for example, the probability \(\Pr(Y = 1 | X = x) = \mu\) increases as \(x\) increases and, for larger values of \(\beta_1\), it rises from 0 to 1 sharply as \(x\) ascends over a very narrow range of values. When we have more than one predictor variable, i.e. \(p > 1\), we assess the relationships between the probability \(\Pr(Y = 1 | X_1=x_1, \ldots, X_p=x_p) = \mu\) and the predictor variables \(X_j\) one-at-a-time by considering what happens when only \(X_j\) varies, so that we need only consider the sign and magnitude of the corresponding \(\beta_j\).
Notice that although in this chapter we only consider continuous predictor variables \(X_j\), we can incorporate categorical predictor variables, interaction terms, non-linear transformations of predictors, and so on, in exactly the same way as for multiple linear regression studied previously.
3.2 Fitting the Model
In general, we do not know the values of the regression coefficients \(\beta_0,\beta_1,\ldots,\beta_p\) in the logistic regression model. However, if we have appropriate training data \((\boldsymbol{x}_1, y_1),\ldots,(\boldsymbol{x}_n, y_n)\) where \(\boldsymbol{x}_i = (x_{i1}, \ldots, x_{ip})\) is the set of \(p\) predictor variables for individual / item \(i\), we can use them to generate estimates \(\hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_p\) for the regression coefficients. One method – maximum likelihood estimation – will be considered briefly below.
3.3 Prediction from the Fitted Model
Suppose we want to classify a new (partial) observation, i.e. given \((x_{\text{new},1}, \ldots, x_{\text{new},p})\) we want to predict the associated value of \(Y_{\text{new}}\). Once we have estimates \(\hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_p\) of the regression coefficients, we can base this prediction on the estimated probability \[\begin{equation*} \hat{\Pr}(Y_{\text{new}} = 1 | X_{\text{new},1}=x_{\text{new},1}, \ldots, X_{\text{new},p}=x_{\text{new},p}) = \frac{\exp(\hat{\beta}_0 + \hat{\beta}_1 x_{\text{new},1} + \ldots + \hat{\beta}_p x_{\text{new},p})}{1 + \exp(\hat{\beta}_0 + \hat{\beta}_1 x_{\text{new},1} + \ldots + \hat{\beta}_p x_{\text{new},p})} \end{equation*}\] by constructing a classification rule of the form: \[\begin{equation} Y_{\text{new}} = \begin{cases} 1, \quad \text{if $\hat{\Pr}(Y_{\text{new}} = 1 | X_{\text{new},1}=x_{\text{new},1}, \ldots, X_{\text{new},p}=x_{\text{new},p}) > \alpha$,}\\ 0, \quad \text{otherwise}. \end{cases}\tag{3.1} \end{equation}\] Most often \(\alpha = 0.5\) but if the “cost” of one of the two classification errors (misclassifying a true 0 as a 1 or a true 1 as a 0) is higher than the other, then a different value for \(\alpha\) may be chosen to adjust the classification decision in an appropriate way.
3.4 Estimation by Maximum Likelihood
The standard approach for producing estimates \(\hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_p\) of the regression coefficients in the logistic regression model is to use a widely used method in statistical inference called maximum likelihood estimation. Although we omit the mathematical details, we note that one of the advantages of this method is that maximum likelihood estimators have a number of nice theoretical properties which can be exploited to derive confidence intervals for the regression coefficients, perform hypothesis tests, and so on. In R, all this goes on under the hood when we use the glm function to fit the logistic regression model. When using the glm function, we need to set the argument family="binomial" to indicate that we want to fit a logistic regression model, and not some other kind of generalised linear model.
3.5 Extension to \(K > 2\)
When the categorical variable has \(K>2\) possible values, it is possible to derive extensions of logistic regression, such as multinomial logistic regression. However, these methods tend not to be used very often because discriminant analysis is much more popular for multiple-class classification. Although they will not be considered further in this module, note that there are R packages available for performing multinomial logistic regression, such as nnet and mlogit.
3.6 Example: Chapman Data
The Chapman data arose from a study on heart disease by Dr. John M. Chapman in the mid-twentieth century. The data were taken from the Los Angeles Heart Study and comprise measurements from \(n=200\) men on \(p=7\) variables. One of these variables is binary, indicating whether or not the patient experienced a coronary incident in the preceding 10 years. There are also six predictor variables, which can be treated as continuous, namely the patient’s age, height and weight and measurements of their cholesterol, systolic and diastolic blood pressure. The idea here is to help in identifying and describing relationships between the predictor variables and incidence of a heart attack.
The data are available from the durhamSLR package in the chapman data set. If you haven’t already done so, please follow the instructions in the Labs for Week 3 to install the durhamSLR package. Once the package is installed, it can be loaded in the usual way, and so we load and inspect the data as follows:
## Load package:
library(durhamSLR)
## Load data:
data(chapman)
## Check size:
dim(chapman)## [1] 200 7## Print first 3 rows:
head(chapman, 3)## Tabulate the categorical variable:
table(chapman$y)##
## 0 1
## 174 26The coding \(y=0\) indicates that a coronary incident was not experienced and conversely for \(y=1\). So we see that 26 of the 200 patients experienced a coronary incident.
We can get a feel for the data by producing a pairs plot of the predictor variables, using colour to distinguish between the two groups of patients:
pairs(chapman[,1:6], col=chapman[,7]+1)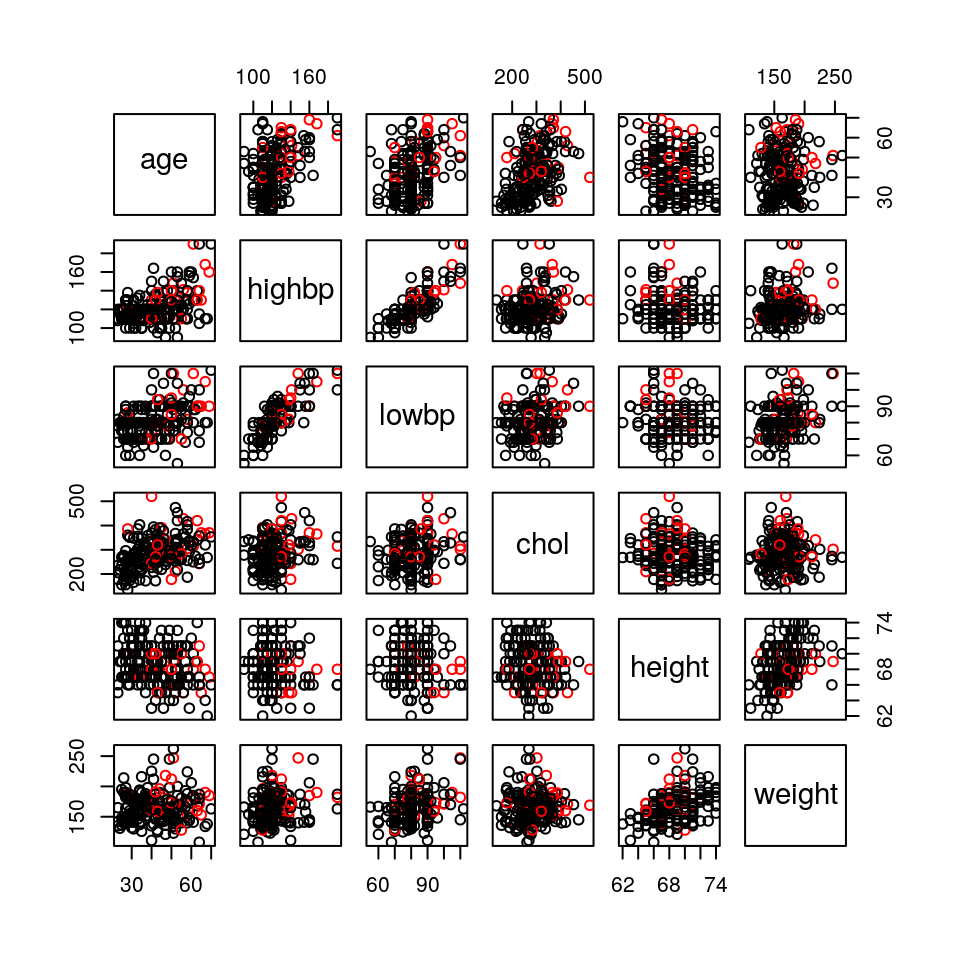
Figure 3.2: Scatterplot matrix for the Chapman data. Patients who did / did not experience a coronary incident appear in red / black.
This generates the plot in Figure 3.2. There is arguably some evidence of a higher incidence of heart attacks amongst older patients but, in general, it is difficult to spot relationships with the response. However, it is immediately clear that the two sets of blood pressure measurements are highly correlated and so any regression model is unlikely to require both.
We can fit a logistic regression model using the glm function. The syntax is almost identical to that of the lm function for multiple linear regression, except we need to remember to set the argument family="binomial" so that R knows to perform logistic regression.
## Fit logistic regression model:
lr_fit = glm(y ~ ., data=chapman, family="binomial")
## Summarise the model fit:
summary(lr_fit)##
## Call:
## glm(formula = y ~ ., family = "binomial", data = chapman)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1130 -0.5541 -0.3907 -0.2527 2.6811
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -4.517321 7.481215 -0.604 0.5460
## age 0.045900 0.023535 1.950 0.0511 .
## highbp 0.006856 0.020198 0.339 0.7343
## lowbp -0.006937 0.038352 -0.181 0.8565
## chol 0.006306 0.003632 1.736 0.0825 .
## height -0.074002 0.106214 -0.697 0.4860
## weight 0.020142 0.009871 2.041 0.0413 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 154.55 on 199 degrees of freedom
## Residual deviance: 134.85 on 193 degrees of freedom
## AIC: 148.85
##
## Number of Fisher Scoring iterations: 5The maximum likelihood estimates of the regression coefficients are therefore
\[\begin{alignat*}{4}
\hat{\beta}_0&=-4.517,&\quad \hat{\beta}_1&=0.046,&\quad \hat{\beta}_2&=0.007,&\quad \hat{\beta}_3&=-0.007,\\
\hat{\beta}_4&=0.006,&\quad \hat{\beta}_5&=-0.074,&\quad \hat{\beta}_6&=0.02.&&
\end{alignat*}\]
Consider, for example, the coefficient for the age variable. Because it is positive, this indicates that older patients are generally more likely to experience a coronary incident.
If we examine the table produced by the summary function we see that a number of the variables have very large \(p\)-values meaning that, individually, they contribute very little to a model which contains all the other predictors. Like in linear regression, inclusion of more predictors than are necessary can inflate the variance of the parameter estimators leading to a deterioration in predictive performance. There are classical methods that can be used to eliminate predictors based on techniques such as analysis of deviance, which we will not consider. Alternatively, we can appeal to techniques like best subset selection that we studied in the previous chapter in the context of linear regression. We will return to this idea in the computer labs for this week.
\[\begin{align*} \hat{\Pr}(Y_{\text{new}} = 1 | X_{\text{new},1}=x_{\text{new},1}, \ldots, X_{\text{new},p}=x_{\text{new},p}) &= \frac{\exp(-4.517 + 0.046 \times 51 + \ldots + 0.02 \times 150)}{1 + \exp(-4.517 + 0.046 \times 51 + \ldots + 0.02 \times 150)}\\ &= 0.108. \end{align*}\]
We can perform this prediction in R as follows
## Set up data frame of predictor variables
x1 = data.frame(age=51, highbp=146, lowbp=72, chol=320, height=74, weight=150)
## Perform prediction
(p1 = predict(lr_fit, x1, type="response"))## 1
## 0.1079599Notice that when using the predict function, we need to set the argument type="response" to get the predicted probability. The default is a prediction of the linear predictor \(\eta\).
As the predicted probability is less than 0.5, if we apply the “standard” classification rule (3.1), we would classify \(Y_{\text{new}} = 0\):
(y = as.numeric(ifelse(p1 > 0.5, 1, 0)))## [1] 04 Discriminant Analysis
4.1 Discriminant Functions
Discriminant analysis requires a discriminant function for each group, \(k=1,\ldots,K\), which we denote by \(Q_k\). Consider a vector of \(p\) predictor variables, which it is convenient to write as \[\begin{equation*} \boldsymbol{x} = \begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_p \end{pmatrix} = (x_1, x_2, \ldots, x_p)^T. \end{equation*}\] When we input \(\boldsymbol{x}\) into each of the discriminant functions, the output is a real number, so we would get \(K\) real numbers \(Q_1(\boldsymbol{x}), \ldots, Q_K(\boldsymbol{x})\). For the different values \(\boldsymbol{x} = (x_1, \ldots, x_p)^T\) that \(\boldsymbol{X} = (X_1, \ldots, X_p)^T\) can take, one of the \(K\) real numbers, say \(Q_k(\boldsymbol{x})\), will be larger than the others. We use this idea to divide up the whole space of values that \(\boldsymbol{X}\) can take into \(K\) non-overlapping parts, \(R_1,R_2,\ldots,R_K\), (called allocation regions) according to the rule \[\begin{equation*} \text{if } Q_k(\boldsymbol{x}) > Q_{\ell}(\boldsymbol{x}), \text{ for all $\ell \ne k$, then $\boldsymbol{x}$ lies in $R_k$}. \end{equation*}\] If \(\boldsymbol{x}\) lies in \(R_k\) then we assign \(Y = k\).
When trained on a particular data set, different discriminant functions will lead to different allocation regions and the allocation regions created by some methods are likely to be more effective than others for correctly predicting the group in which a new observation lies.
The so-called Bayes classifier is based on (2.4) and simply assigns an observation \(\boldsymbol{x}\) to the class \(k\) for which the posterior probability \(p_k(\boldsymbol{x}) = \Pr(Y = k | \boldsymbol{X} = \boldsymbol{x}) = \Pr(Y = k | X_1 = x_1, \ldots, X_p = x_p)\) is largest. It can be shown that this is equivalent to assigning \(\boldsymbol{x}\) to class \(k\) if and only if \[\begin{align*} f_k(\boldsymbol{x}) \pi_k > f_{\ell}(\boldsymbol{x}) \pi_{\ell} \end{align*}\] for all \(\ell \ne k\). Therefore the corresponding discriminant functions are \[\begin{equation*} Q_k(\boldsymbol{x}) = f_k(\boldsymbol{x}) \pi_k, \quad k=1,\ldots,K. \end{equation*}\] In the special case when all the prior group probabilities are equal, i.e. \(\pi_1 = \pi_2 = \ldots = \pi_K = 1/K\), the discriminant functions simplify to \[\begin{equation*} Q_k(\boldsymbol{x}) = f_k(\boldsymbol{x}), \quad k=1,\ldots,K. \end{equation*}\] In this case the resulting rule for classification is called the maximum likelihood discriminant rule because an observation is assigned to the group with the maximum likelihood.
4.2 The Multivariate Normal Distribution: A Concise Summary
A random p-vector \(\boldsymbol{X} = (X_1,\ldots,X_p)^T\) is a \(p\)-dimensional vector whose elements, \(X_1,\ldots,X_p\), are all random variables. It is called a continuous random vector if all the \(X_j\) are continous and a discrete random vector if all the \(X_j\) are discrete. The normal distribution is a model for a continuous random variable \(X\). The multivariate normal distribution provides a generalisation for a continuous random vector \(\boldsymbol{X}\) with \(p>1\). Here we provide a very concise summary.
Recall from the first half of this module that if a random variable \(X\) has a normal distribution with mean \(\mu\) and variance \(\sigma^2\), written \(X \sim \mathrm{N}(\mu, \sigma^2)\), then its probability density function is given by \[\begin{equation*} f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left\{ -\frac{1}{2 \sigma^2}(x-\mu)^2 \right\}. \end{equation*}\] For example, if \(\mu=0\) and \(\sigma^2=1\), a plot of the probability density function is shown in the left-hand image of Figure 4.1. Recall that the probability of \(X\) taking a value between \(a\) and \(b\) is just the area under the curve between \(a\) and \(b\) as indicated in the right-hand plot of Figure 4.1. Therefore \(X\) is more likely to take values in regions where the density function is large.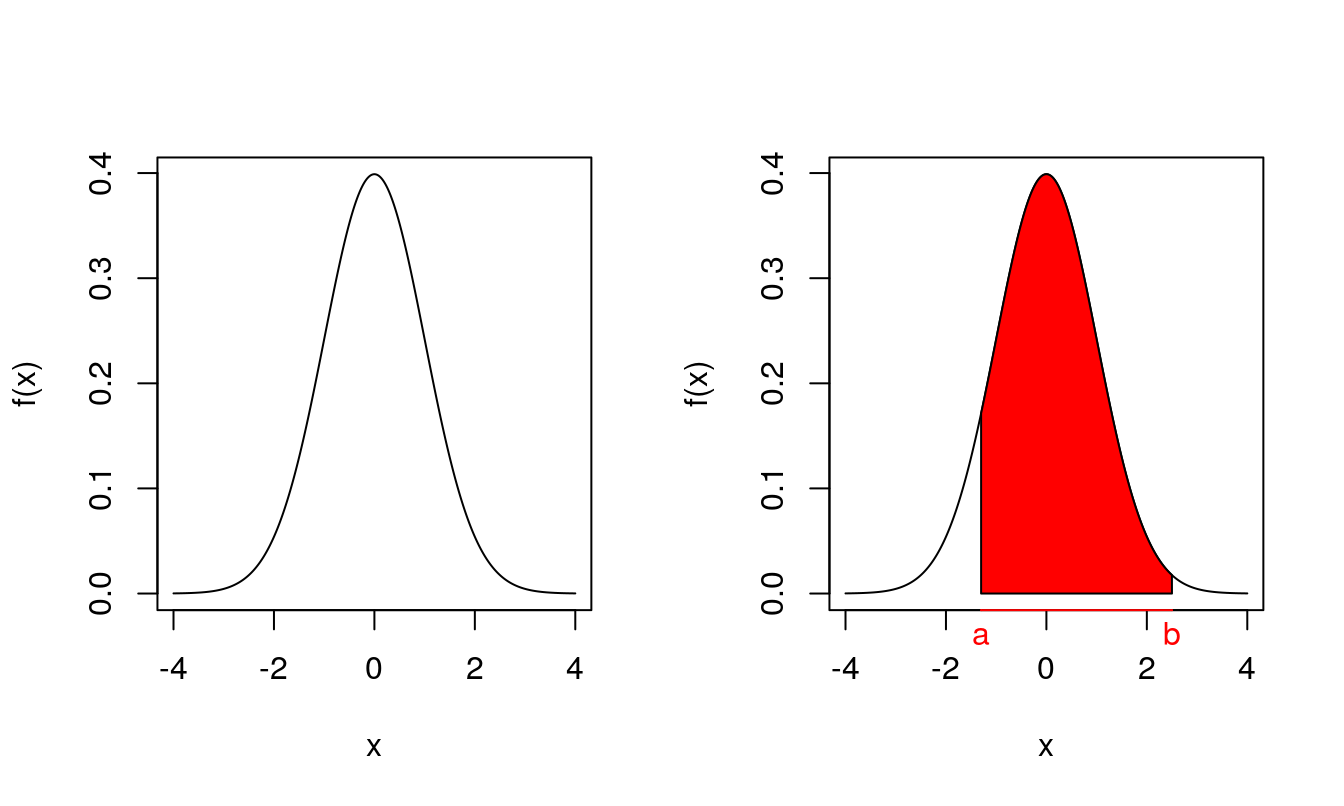
Figure 4.1: Left: probability density function for the (univariate) normal distributions when \(\mu=0\) and \(\sigma^2=1\). Right: the area of the shaded region is \(\Pr(a \le X \le b)\).
If \(\boldsymbol{X} = ( X_1, X_2, \ldots, X_p )^T\) is a random \(p\)-vector, it does not have a single mean and a single variance. Instead, there is a mean \(\mu_j\) for each random variable \(X_j\). These are collected into a length-\(p\) column vector \(\boldsymbol{\mu} = (\mu_1, \mu_2, \ldots, \mu_p)^T\). Similarly, each \(X_j\) has its own variance \(\sigma_{jj}\) and every pair of random variables \(X_j\) and \(X_k\) has a covariance \(\sigma_{jk}\) which provides information about the relationship between \(X_j\) and \(X_k\), e.g. its sign indicates whether there is a positive or negative correlation. These variances and covariances are collected into a \(p \times p\) covariance matrix \[\begin{equation*} \Sigma = \begin{pmatrix} \sigma_{11} &\sigma_{12} &\cdots &\sigma_{1p}\\ \sigma_{21} &\sigma_{22} &\cdots &\sigma_{2p}\\ \vdots &\vdots &\ddots &\vdots\\ \sigma_{p1} &\sigma_{p2} &\cdots &\sigma_{pp}\\ \end{pmatrix} \end{equation*}\] which is symmetric (meaning \(\sigma_{ij} = \sigma_{ji}\)) and positive definite (the matrix analogue of “positive”).
Now, if a random \(p\)-vector \(\boldsymbol{X} = ( X_1, X_2, \ldots, X_p )^T\) has a multivariate normal distribution with mean vector \(\boldsymbol{\mu}\) and covariance matrix \(\Sigma\), written \(\boldsymbol{X} \sim \mathrm{N}_p(\boldsymbol{\mu}, \Sigma)\), then its probability density function is given by \[\begin{equation*} f(\boldsymbol{x}) = \frac{1}{(2 \pi)^{p/2} | \Sigma |^{1/2}} \exp \left\{ -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right\}. \end{equation*}\] This expression involves matrix algebra, but the important thing to note is that for any value \(\boldsymbol{x}\), \(f(\boldsymbol{x})\) is just a real number. For example, if \(p=2\) we have a bivariate normal distribution and can generate a 3-dimensional plot to show the probability density function. For two sets of values for the parameters, \(\boldsymbol{\mu}\) and \(\Sigma\), density functions are displayed in Figure 4.2. Just like in the univariate case, the probability that \(X_1\) lies between \(a_1\) and \(b_1\) and that \(X_2\) lies between \(a_2\) and \(b_2\) is just the volume under the surface over the rectangular region with corners at \((a_1, a_2)\), \((a_1, b_2)\), \((b_1, b_2)\) and \((b_1, a_2)\). Again \(\boldsymbol{X}=(X_1, X_2)^T\) is more likely to take values in regions where the density function is large.
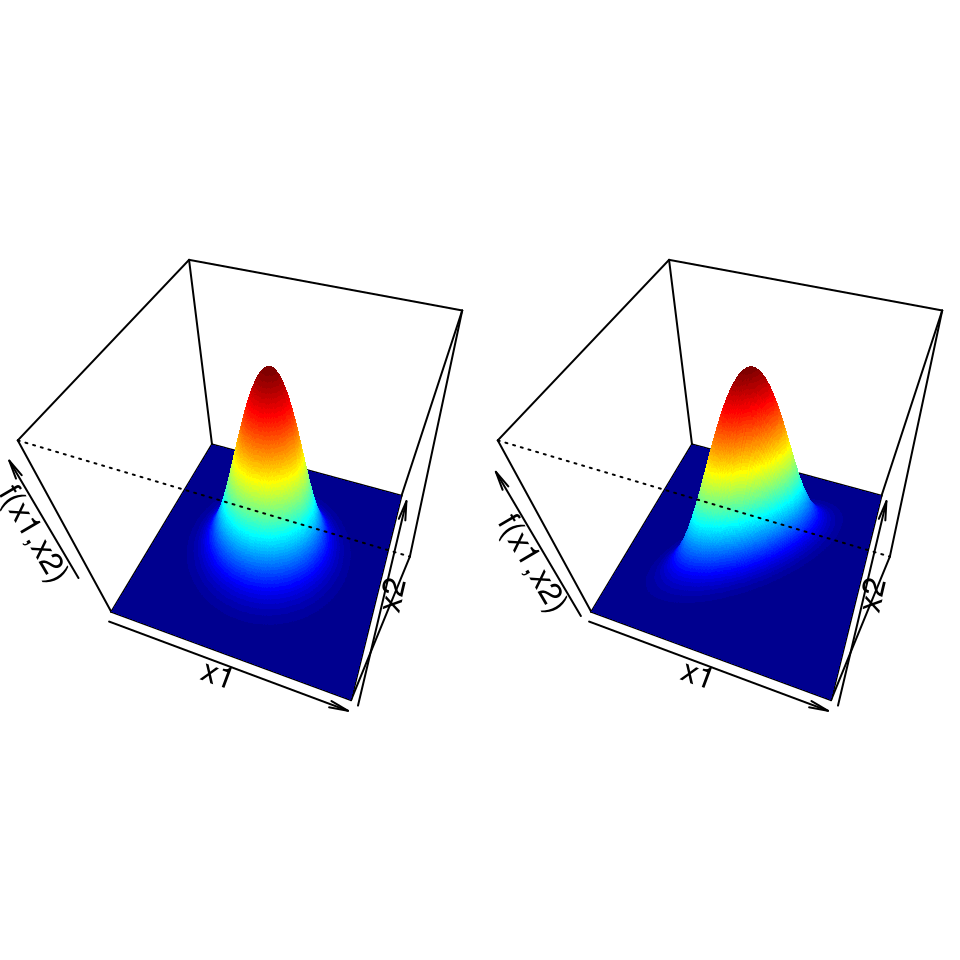
Figure 4.2: Probability density functions for two bivariate normal distributions. Left: \(X_1\) and \(X_2\) are uncorrelated; right: the correlation between \(X_1\) and \(X_2\) is 0.7.
4.3 Linear Discriminant Analysis (LDA)
LDA classifiers assume that the conditional distributions for the predictor variables \(\boldsymbol{X} = ( X_1, X_2, \ldots, X_p )^T\) are multivariate normal, with a group-specific mean vector and a common covariance matrix: \[\begin{equation*} \boldsymbol{X} | Y = k \sim \mathrm{N}_p(\boldsymbol{\mu}_k, \Sigma) \end{equation*}\] for \(k=1,\ldots,K\). The Bayes classifier for LDA therefore uses the discriminant functions \[\begin{equation*} Q_k(\boldsymbol{x}) = f_k(\boldsymbol{x}) \pi_k = \frac{1}{(2\pi)^{p/2} |\Sigma|^{1/2}} \exp\left\{-\frac{1}{2}\left(\boldsymbol{x} - \boldsymbol{\mu}_k\right)^T \Sigma^{-1} \left(\boldsymbol{x} - \boldsymbol{\mu}_k \right)\right\} \pi_k \end{equation*}\] for groups \(k=1,\dots,K\). We assign \(\boldsymbol{x}\) to the group \(k\) for which \(Q_k(\boldsymbol{x})\) is largest.
After applying some algebraic manipulation, it can be shown that this is equivalent to using \[\begin{equation} Q_k(\boldsymbol{x}) = \boldsymbol{\mu}_k^T \Sigma^{-1} \boldsymbol{x} - \frac{1}{2} \boldsymbol{\mu}_k^T \Sigma^{-1} \boldsymbol{\mu}_k + \log \pi_k, \quad \text{for $k=1,\ldots,K$}\tag{4.1} \end{equation}\] which are linear in \(\boldsymbol{x}\). This is where the word linear in linear discriminant analysis comes from. For those unfamiliar with matrix algebra, this is simplest to see in the case when \(p=1\) so that \(\boldsymbol{x}=x\), \(\boldsymbol{\mu}_k = \mu_k\) and \(\Sigma = \sigma^2\) are just real numbers. In this case (4.1) simplifies to \[\begin{equation*} Q_k(x) = \frac{\mu_k}{\sigma^2} x - \frac{\mu_k^2}{2 \sigma^2} + \log \pi_k = a_k x + b_k, \end{equation*}\] for \(k=1,\ldots,K\), where \(a_k = \mu_k / \sigma^2\) and \(b_k = \log \pi_k - \mu_k^2 / (2 \sigma^2)\) are constants. This is just the equation of a straight line with intercept and gradient that depend on the group \(k\).

Figure 4.3: Illustrative example of allocation regions in LDA when \(K=3\) and \(p=1\).
The boundaries between the allocation regions \(R_k\) and \(R_{\ell}\) are called the decision boundaries of the classifier. They can be calculated by finding those values of \(\boldsymbol{x}\) that satisfy \(Q_k(\boldsymbol{x}) = Q_\ell(\boldsymbol{x})\). If \(p=1\), the solution is a point on the real line; if \(p=2\), it is a straight line in the \((x_1, x_2)\)-plane; if \(p=3\), it is a plane (i.e. a flat surface) in 3-dimensional \((x_1, x_2, x_3)\)-space; and so on. For example, if there were \(K=3\) groups and \(p=1\), we might get allocation regions like those illustrated in Figure 4.3. If \(K=3\) and \(p=2\), we might get allocation regions like those in Figure 4.4.
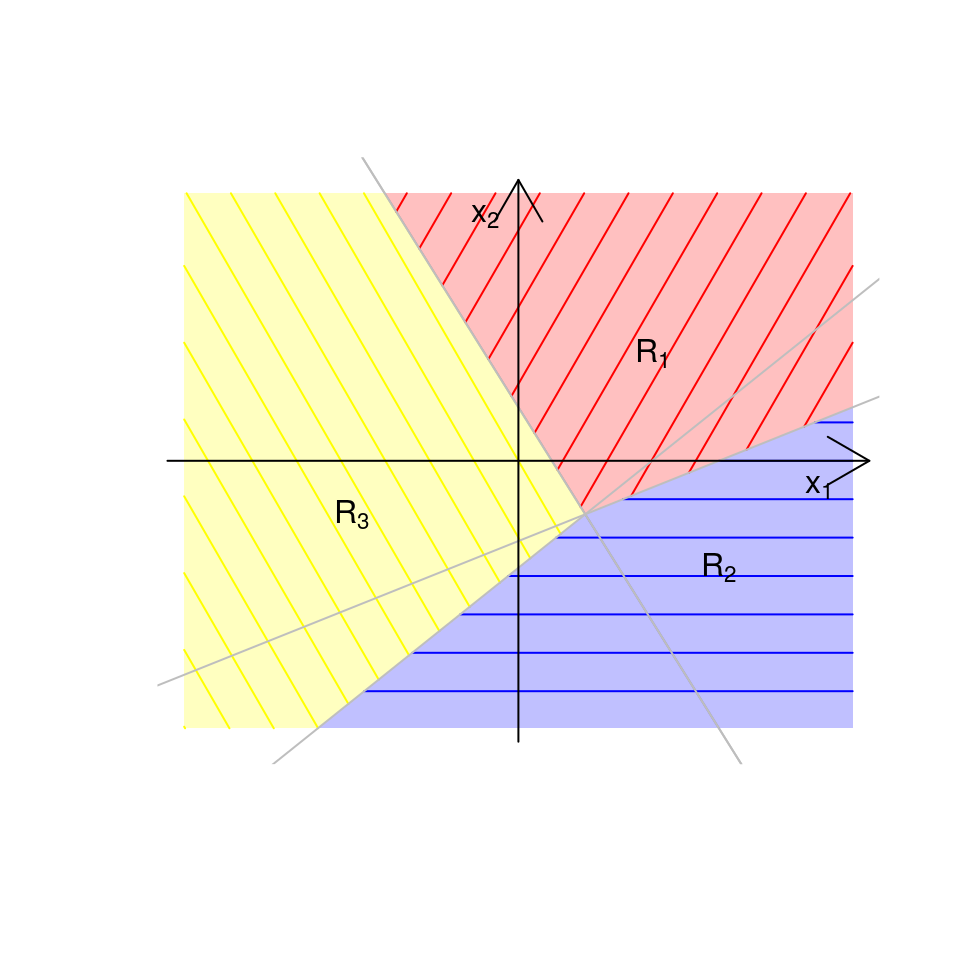
Figure 4.4: Illustrative example of allocation regions in LDA when \(K=3\) and \(p=2\).
4.4 Quadratic Discriminant Analysis (QDA)
As discussed in the previous section, in LDA we assume that the conditional distributions for the predictor variables \(\boldsymbol{X}\) are multivariate normal, with a group-specific mean vector and a common covariance matrix. Quadratic discriminant analysis (QDA) is similar except the different groups are allowed to have different covariance matrices. In other words we assume that \[\begin{equation*} \boldsymbol{X} | Y = k \sim \mathrm{N}_p(\boldsymbol{\mu}_k, \Sigma_k) \end{equation*}\] for \(k=1,\ldots,K\). The Bayes classifier for QDA therefore uses the discriminant functions \[\begin{equation*} Q_k(\boldsymbol{x}) = f_k(\boldsymbol{x}) \pi_k = \frac{1}{(2\pi)^{p/2} |\Sigma_k|^{1/2}} \exp\left\{-\frac{1}{2}\left(\boldsymbol{x} - \boldsymbol{\mu}_k\right)^T \Sigma_k^{-1} \left(\boldsymbol{x} - \boldsymbol{\mu}_k \right)\right\} \pi_k \end{equation*}\] for groups \(k=1,\dots,K\). We assign \(\boldsymbol{x}\) to the group \(k\) for which \(Q_k(\boldsymbol{x})\) is largest.
Again, we can apply some algebraic manipulation, to show that this is equivalent to using \[\begin{equation} Q_k(\boldsymbol{x}) = - \frac{1}{2} \boldsymbol{x}^T \Sigma_k^{-1} \boldsymbol{x} + \boldsymbol{\mu}_k^T \Sigma_k^{-1} \boldsymbol{x} - \frac{1}{2} \boldsymbol{\mu}_k^T \Sigma_k^{-1} \boldsymbol{\mu}_k - \frac{1}{2} \log |\Sigma_k| + \log \pi_k, \quad k=1,\ldots,K\tag{4.2} \end{equation}\] which are quadratic in \(\boldsymbol{x}\). This is where the word quadratic in quadratic discriminant analysis comes from. This is simplest to see in the case when \(p=1\) so that \(\boldsymbol{x}=x\), \(\boldsymbol{\mu}_k = \mu_k\) and \(\Sigma_k = \sigma_k^2\) are just real numbers. In this case (4.2) simplifies to \[\begin{align*} Q_k(x) &= - \frac{1}{2 \sigma_k^2} x^2 + \frac{\mu_k}{\sigma_k^2} x - \frac{\mu_k^2}{2 \sigma_k^2} - \frac{1}{2} \log \sigma_k^2 + \log \pi_k\\ &= a_k x^2 + b_k x + c_k, \end{align*}\] for \(k=1,\ldots,K\), where \(a_k = -1 / (2 \sigma_k^2)\), \(b_k= \mu_k / \sigma_k^2\) and \(c_k = \log \pi_k - \mu_k^2 / (2 \sigma_k^2) - (\log \sigma_k^2) / 2\) are constants. This is just the equation of a quadratic curve.
The decision boundaries between the allocation regions \(R_k\) and \(R_{\ell}\) are, again, calculated by finding those values of \(\boldsymbol{x}\) that satisfy \(Q_k(\boldsymbol{x}) = Q_\ell(\boldsymbol{x})\). For example, if we had \(K=2\) groups and \(p=2\), we might get something which looks like the plot in Figure 4.5 where we see a quadratic boundary between the two allocation regions.
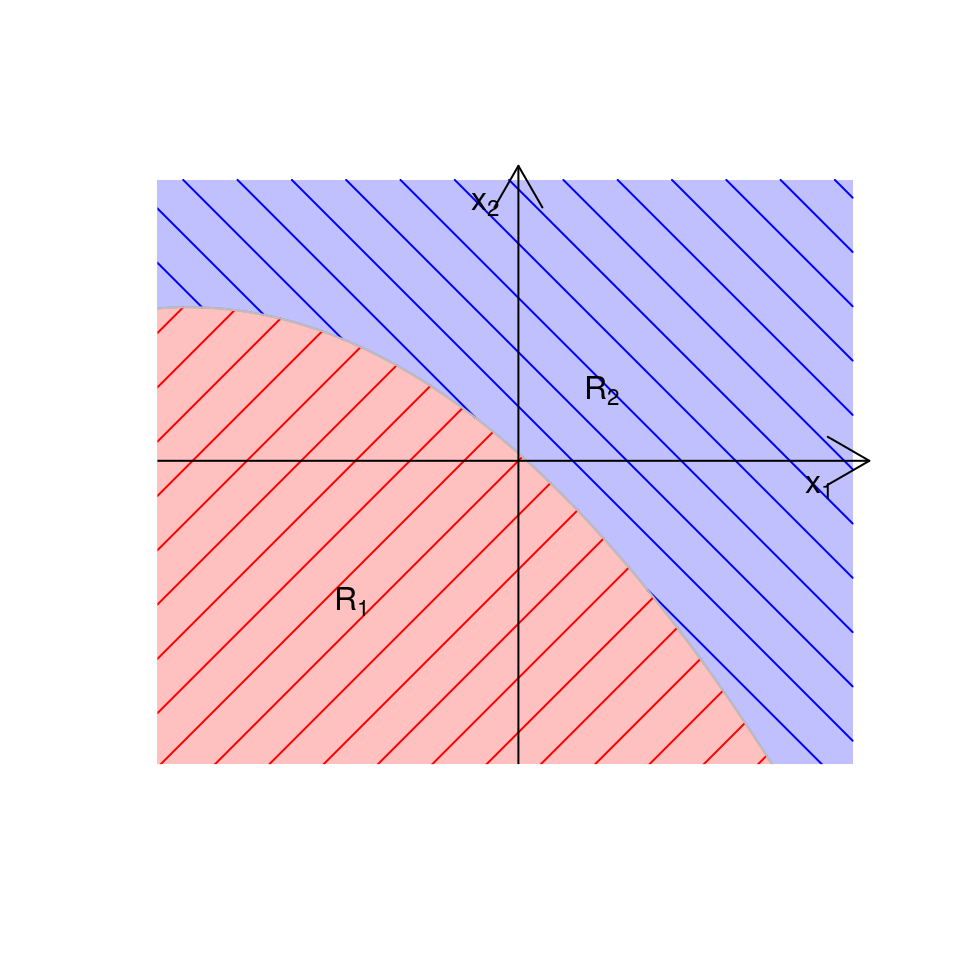
Figure 4.5: Illustrative example of allocation regions in QDA when \(K=2\) and \(p=2\).
4.5 Fitting the Model
In practice, we generally do not know the group mean vectors \(\boldsymbol{\mu}_k\) or the common covariance matrix \(\Sigma\) in the conditional distributions \[\begin{equation*} \boldsymbol{X} | Y = k \sim \mathrm{N}_p(\boldsymbol{\mu}_k, \Sigma) \end{equation*}\] for LDA, or the group mean vectors \(\boldsymbol{\mu}_k\) and group covariance matrices \(\Sigma_k\) in the conditional distributions \[\begin{equation*} \boldsymbol{X} | Y = k \sim \mathrm{N}_p(\boldsymbol{\mu}_k, \Sigma_k) \end{equation*}\] for QDA. Similarly, we often do not know in advance the prior group membership probabilities \(\pi_k\) in the Bayes classifiers for LDA or QDA. However, these parameters can often be estimated from data that has already been classified. Recall that we refer to this as a training set.
The details of this estimation procedure for the mean vectors and covariance matrices are beyond the scope of this course. For the group membership probabilities \(\pi_k\), one method of estimation is to use the sample proportions which we can estimate as follows. Suppose we have training data, \((\boldsymbol{x}_1, y_1),\ldots,(\boldsymbol{x}_n, y_n)\) where \(\boldsymbol{x}_i\) contains the observations on the \(p\) predictor variables for individual / item \(i\). If \(n_k\) of the observations are from group \(k\) (i.e. have \(y_i=k\)) then we can replace \(\pi_k\) in our discriminant functions with estimates \[\begin{equation*} \hat{\pi}_k = \frac{n_k}{n}, \quad k=1,\ldots,K. \end{equation*}\] However, clearly this will not be appropriate if our training data do not form a representative sample of group labels. This might occur in a clinical trial, for instance, if we deliberately choose a sample of healthy patients and another sample of patients with a particular disease. In this case, the sample proportion of diseased individuals would be much higher than that in the wider population! In situations like these we must use estimates of the group membership probabilities that have been obtained by other means. For instance, in the clinical trial example, doctors may have some idea about the incidence of disease in the population as a whole.
4.6 Example: MBA Admissions Data
The MBA admissions data are available from the durhamSLR package as the admission data set. The data concern applicants to the Masters of Business Administration (MBA) programme of a US business graduate school. For each of a random sample of 85 applicants, the category to which the student was assigned by admissions tutors is recorded (admit, borderline or do not admit) along with the student’s grade point average (GPA) and graduate management admission test (GMAT) score. (The GPA is an average of the student’s results earned during their undergraduate degree and can range from 0.0 to 4.0. The GMAT is a standardised exam designed to assess skills deemed important for an MBA and scores range from 200 to 800.)
Loading the data into R and printing the first few rows yields
## Load data into R
data(admission)
## Print the first few rows
head(admission)Suppose we want to use these data to generate a rule for automatic classification of applicants. In this case we have three groups (\(K=3\)) and \(p=2\) variables (\(X_1 = \text{GPA}\) and \(X_2 = \text{GMAT}\)).
We begin by plotting the data
plot(admission$GPA, admission$GMAT, col=as.numeric(admission$decision)+1,
pch=as.numeric(admission$decision), xlab="GPA", ylab="GMAT",
ylim=c(200, 800), xlim=c(2,4))
legend("topleft", c("admit","borderline","not admit"), col=2:4, pch=1:3)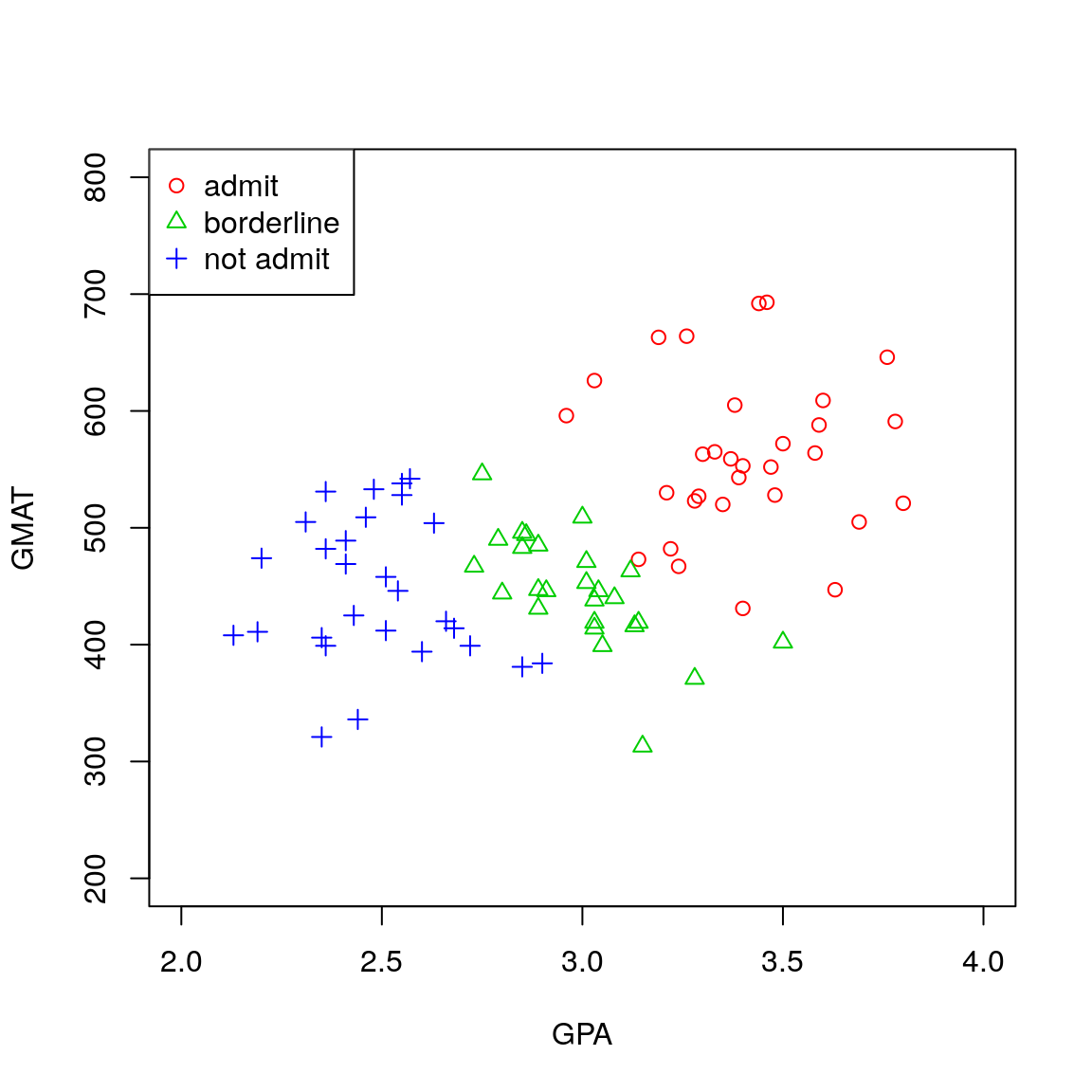
Figure 4.6: Scatterplot for the MBA admissions data.
which generates the scatterplot in Figure 4.6. An assumption of equal variance amongst the three groups does not seem unreasonable here and so we will generate the rule for automatic classification using the Bayes classifier for LDA.
We can estimate the parameters in our Bayes classifier for LDA using the lda function from the MASS package in R.
## Load the MASS package
library(MASS)
## Perform LDA
(lda_fit = lda(decision ~ ., data=admission))## Call:
## lda(decision ~ ., data = admission)
##
## Prior probabilities of groups:
## admit border notadmit
## 0.3647059 0.3058824 0.3294118
##
## Group means:
## GPA GMAT
## admit 3.403871 561.2258
## border 2.992692 446.2308
## notadmit 2.482500 447.0714
##
## Coefficients of linear discriminants:
## LD1 LD2
## GPA 5.008766354 1.87668220
## GMAT 0.008568593 -0.01445106
##
## Proportion of trace:
## LD1 LD2
## 0.9673 0.0327## Is the output a list?
is.list(lda_fit)## [1] TRUE## What are its components?
names(lda_fit)## [1] "prior" "counts" "means" "scaling" "lev" "svd" "N" "call" "terms" "xlevels"The output lda_fit is a list and the estimates of the prior group membership probabilities \(\hat{\pi}_k\) for \(k=1,2,3\) are stored in the component called prior, which we can extract as follows
## Extract prior component of lda_fit object
lda_fit$prior## admit border notadmit
## 0.3647059 0.3058824 0.3294118## Compare to sample proportions
table(admission$decision) / nrow(admission)##
## admit border notadmit
## 0.3647059 0.3058824 0.3294118We therefore see that by default, R will use the sample proportions to estimate the prior group membership probabilities. If this is not appropriate, we can supply our own estimates of the prior group membership probabilities by passing an argument called prior to the lda function. We shall see an example of this in Section 5.3.3.
The estimates of the group specific mean vectors \(\boldsymbol{\hat{\mu}}_k\) for \(k=1,2,3\) are stored in the component called means
## Extract the group specific means
lda_fit$means## GPA GMAT
## admit 3.403871 561.2258
## border 2.992692 446.2308
## notadmit 2.482500 447.0714As we saw in Figure 4.6, the means for both test scores are the largest in the admit group. The mean GMAT scores are very similar in the border and notadmit groups but the mean GPA score is notably smaller in the notadmit group than the border group.
The so-called Coefficients of linear discriminants are stored in the component called scaling
## Extract the coefficients of linear discriminants
lda_fit$scaling## LD1 LD2
## GPA 5.008766354 1.87668220
## GMAT 0.008568593 -0.01445106It is tempting to think that the coefficients of linear discriminants might be coefficients in the discriminant functions. However, this is not the case. They actually arise through a slightly different way of formulating the problem addressed in linear discriminant analysis (called Fisher’s linear discriminant) which we do not cover in this module.
If the coefficients of linear discriminants do not give the coefficients in the discriminant functions, where can this information be found? Unfortunately, the discriminant functions are not returned by functions in theMASS package or any of the other popular R packages for implementing LDA or QDA. Nevertheless, it is possible to write an R function to calculate them. Though the details are beyond the scope of this course, for illustration in this example, the discriminant functions for groups 1 (admit), 2 (border) and 3 (notadmit) can be calculated as
\[\begin{align*}
Q_1(\boldsymbol{x}) &= -241.380 + 106.250 x_1 + 0.212 x_2\\
Q_2(\boldsymbol{x}) &= -178.500 + 92.670 x_1 + 0.173 x_2\\
Q_3(\boldsymbol{x}) &= -135.009 + 78.086 x_1 + 0.165 x_2
\end{align*}\]
By solving \(Q_j(\boldsymbol{x}) = Q_k(\boldsymbol{x})\) for all pairs \(j \ne k\) we can derive the boundaries between the allocation regions and hence display the allocation regions \(R_1, R_2, R_3\) on a plot. This is illustrated in Figure 4.7.
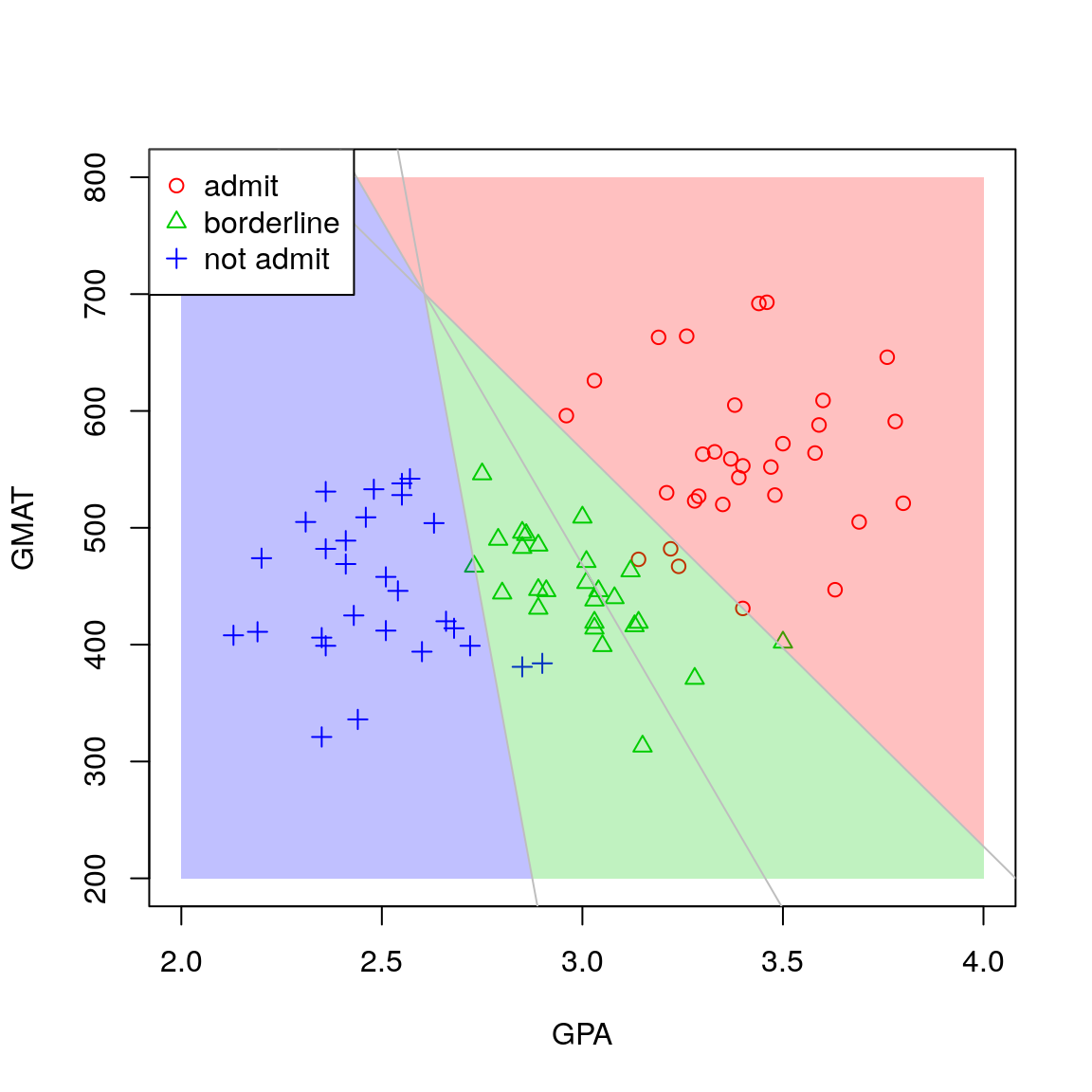
Figure 4.7: Scatterplot for the MBA admissions data with admissions regions.
For example, suppose we would like to classify a new applicant with GPA 3.5 and GMAT score 500. We see immediately from Figure 4.7 that we would assign the applicant to group 1, i.e. the admit group. We can also perform this classification in R by passing the object returned by the lda function to the predict function. The second argument should be a data frame of predictor values for which classification is required, with columns labelled as per the training data
## Perform classification for a new applicant
(ynew = predict(lda_fit, data.frame(GPA=3.5, GMAT=500)))## $class
## [1] admit
## Levels: admit border notadmit
##
## $posterior
## admit border notadmit
## 1 0.9841421 0.01585776 0.0000001669489
##
## $x
## LD1 LD2
## 1 2.730657 0.8190787The desired group label is contained in the component called class
## Extract group label
ynew$class## [1] admit
## Levels: admit border notadmit5 Assessing Predictive Error and Cross-Validation
5.1 The Misclassification Rate
In any problem involving real data, the classification rules based on logistic regression or discriminant analysis will not characterise the group of interest perfectly, and so when we classify new observations, it is likely that some will be allocated to the wrong group. An obvious way to measure the predictive performance of a classification scheme is according to its degree of misclassification. For any model-based classification method we can define a \(K \times K\) matrix \(P\) of classification probabilities with \((i,j)\)th element \[\begin{equation*} p_{ij} = \Pr(\text{allocate to group $j$} \mid \text{observation from group $i$}). \end{equation*}\] In words, \(p_{ij}\) is the probability of allocating an observation from group \(i\) to group \(j\). For a perfect classification scheme, \(P\) would be a \(K \times K\) matrix with 0 in all its off-diagonal elements and 1 in all its diagonal elements. In practice, the best we could hope for would be a matrix with diagonal elements close to 1 and off-diagonal elements close to 0.
Using the \(p_{ij}\) we can calculate the overall misclassification rate as \[\begin{equation*} \text{misclassification rate} = \sum_{i=1}^K \sum_{j \ne i} p_{ij} = \sum_{i=1}^K 1 - p_{ii} \end{equation*}\] This single number summary is typically used to characterise the overall predictive performance of the classifier. The analogue in the context of linear regression is the mean squared error.
For model-based classification schemes in which the model parameters are known (e.g. logistic regression with known regression coefficients or the Bayes classifier for LDA where the group means \(\boldsymbol{\mu}_k\), shared covariance matrix \(\Sigma\) and group membership probabilities \(\pi_k\) are known) it is generally possible to use the probability model to calculate analytic expressions for the \(p_{ij}\) in terms of the model parameters. However, in real-life applications, we will not know the values of the parameters in our classifiers; this is why we estimate their values using data. As a consequence, we cannot calculate exactly the values of the classification probabilities \(p_{ij}\) or the misclassification rate. Again, we therefore estimate the misclassification rate using data.
As in the regression context, we call the data used to construct the classifier our training data, and the data used to estimate the misclassification rate our validation or test data. Suppose we have test data, \((\boldsymbol{x}_1, y_1),\ldots,(\boldsymbol{x}_m, y_m)\) where \(\boldsymbol{x}_i\) contains the observations on the \(p\) predictor variables for individual / item \(i\). A popular method for estimating the classification probabilities \(p_{ij}\), which works even when classifiers are not model-based, is called the empirical method. The empirical method estimates the \(p_{ij}\) with the empirical proportion \[\begin{equation*} \widehat{p_{ij}}=\frac{m_{ij}}{m_i}, \end{equation*}\] where \(m_{ij}=\#(\text{from group $i$ and assigned to group $j$})\) and \(m_i=\sum_{j=1}^K m_{ij}\) is the number of observations in group \(i\). The \(K \times K\) matrix of counts \(m_{ij}\) is often called the confusion matrix. Denote by \(\hat{y}_r\) the group assigned to the \(r\)-th element of the sample by the classifier and by \(y_r\) the group actually observed. The overall misclassification rate can then be estimated as \[\begin{align*} \text{misclassification rate} &\simeq \frac{1}{m} \sum_{r=1}^m \mathbb{I}( \hat{y}_r \ne y_r )\\ &= \frac{1}{m} \sum_{i=1}^K \sum_{j \ne i} m_{ij}\\ &= \frac{1}{m} ( m - \sum_{i=1}^K m_{ii} )\\ &= 1 - \frac{1}{m} \sum_{i=1}^K m_{ii} \end{align*}\] where \(\mathbb{I}(A)\) is an indicator function which evaluates to 1 if \(A\) is true and 0 otherwise.
If the same data are used to both train and validate the classifier (so that the test data are actually the training data), this is called in-sample validation. The resulting confusion matrix and estimate of the misclassification rate are called the training confusion matrix and training error. If the training and test data are different, this is called out-of-sample validation. The resulting confusion matrix and estimate of the misclassification rate are called the test confusion matrix and test error.
5.2 In-Sample Validation
Just like in the regression context, the training error tends to give optimistic estimates of the performance of the classification scheme due to overfitting. This is caused by double-use of the data for constructing and testing the classifier. Nevertheless, it is quick and easy to compute and can be calculated even for a small data set. Moreover, the training confusion matrix can be a helpful tool when building a classifier.
5.2.1 Example: Chapman Data Continued
In Section 3.6, we used the glm function to fit a logistic regression model to the Chapman data:
## Fit logistic regression model:
lr_fit = glm(y ~ ., data=chapman, family="binomial")To calculate the training error we first compute the training confusion matrix by comparing the observed values \(y_1, \ldots, y_n\) with the fitted (i.e. predicted) values \(\hat{y}_1,\ldots, \hat{y}_n\) associated with each set of predictor variables \(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_n\). We calculate the fitted values by using the predict function to compute the predicted probabilities associated with \(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_n\) and then applying our classification rule:
## Compute predicted probabilities:
phat = predict(lr_fit, chapman, type="response")
## Compute fitted (i.e. predicted) values:
yhat = ifelse(phat > 0.5, 1, 0)Now we can produce the (training) confusion matrix by cross-tabulating the observed and fitted values:
## Calculate confusion matrix:
(confusion = table(Observed=chapman$y, Predicted=yhat))## Predicted
## Observed 0 1
## 0 174 0
## 1 24 2If we like, we can also compute the corresponding empirical estimates of the classification probabilities by dividing each row by the row sum:
## Write a function which normalises a vector:
normalise = function(x) {
return(x / sum(x))
}
## Apply the function to each row of the confusion matrix:
t(apply(confusion, 1, normalise))## Predicted
## Observed 0 1
## 0 1.0000000 0.00000000
## 1 0.9230769 0.07692308Note that we misclassify a lot of “true” 1s as 0s, i.e. a lot of patients suffering heart attacks as being heart attack free. The overall training error rate is given by
1 - sum(diag(confusion)) / sum(confusion)## [1] 0.12Or, equivalently,
1 - mean(chapman$y == yhat)## [1] 0.12Here the training error rate is equal to 12%.
5.2.2 Example: MBA Admissions Data Continued
In Section 4.6, we used the lda function from the MASS package in R to fit the Bayes classifier for LDA to the MBA admissions data:
## Train Bayes classifier for LDA:
lda_fit = lda(decision ~ ., data=admission)To calculate the training error we first compute the training confusion matrix by comparing the observed values \(y_1, \ldots, y_n\) with the fitted (i.e. predicted) values \(\hat{y}_1,\ldots, \hat{y}_n\) associated with each set of predictor variables \(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_n\). We calculate the fitted values by using the predict function to classify applicants with predictor variables \(\boldsymbol{x}_1, \ldots, \boldsymbol{x}_n\). Recall that the group labels are contained in the component called class:
## Compute predicted values:
lda_predict = predict(lda_fit, admission)
yhat = lda_predict$classNow we can produce the (training) confusion matrix by cross-tabulating the observed and fitted values:
## Calculate confusion matrix:
(confusion = table(Observed=admission$decision, Predicted=yhat))## Predicted
## Observed admit border notadmit
## admit 28 3 0
## border 1 24 1
## notadmit 0 2 26If we like, we can also compute the corresponding empirical estimates of the classification probabilities by dividing each row by the row sum:
## Apply the function to each row of the confusion matrix:
t(apply(confusion, 1, normalise))## Predicted
## Observed admit border notadmit
## admit 0.90322581 0.09677419 0.00000000
## border 0.03846154 0.92307692 0.03846154
## notadmit 0.00000000 0.07142857 0.92857143The overall training error rate is given by
1 - sum(diag(confusion)) / sum(confusion)## [1] 0.08235294Or, equivalently,
1 - mean(admission$decision == yhat)## [1] 0.08235294Here the training error rate is equal to 8.24%.
Note that if we had instead wanted to use QDA, the MASS package contains the qda function. This is just like the lda function for LDA, with analogous syntax.
5.3 Out-of-Sample Validation
Especially when we have a large number \(n\) of observations, out-of-sample validation provides a more reliable measure of the performance of a classifier than in-sample validation. As in multiple linear regression, two commonly used approaches are
- The validation set approach where we randomly divide the data into a training set, which is used to construct the classifier, and a validation set, on which the test error is computed;
- \(k\)-fold cross-validation where we randomly divide the data into \(k\) folds and compute the average test error obtained by successively holding a single fold back as test data or validation data, with the other folds serving as training data.
In this section we shall see some examples using the validation set approach. In labs, we will explore \(k\)-fold cross-validation.
5.3.1 Example: Chapman Data Continued Again
We will use the validation set approach to estimate the test error for this example. Similarly to the example in the previous chapter, where we were considering the least squares fit of a multiple linear regression model, we can sample the indices for our training and validation data as follows:
## Sample indices of training data:
train_set = sample(c(TRUE, FALSE), nrow(chapman), replace=TRUE)If we have a TRUE in the \(i\)-th position of the vector train_set, the \(i\)-th observation is used in the training data. Otherwise, it is used in the validation data. Next we fit the model to the training data and calculate the fitted values for the validation data:
## Fit logistic regression model to training data:
lr_train = glm(y ~ ., data=chapman[train_set,], family="binomial")
## Compute fitted values for the validation data:
phat_test = predict(lr_train, chapman[!train_set,], type="response")
yhat_test = ifelse(phat_test > 0.5, 1, 0)Now we can produce the (test) confusion matrix by cross-tabulating the observed and fitted values:
## Calculate confusion matrix:
(confusion = table(Observed=chapman$y[!train_set], Predicted=yhat_test))## Predicted
## Observed 0 1
## 0 88 5
## 1 14 2Finally we compute the test error:
1 - mean(chapman$y[!train_set] == yhat_test)## [1] 0.1743119In this example, the test error is larger than the training error, as we would expect.
Recall from the discussion in Section 3.6 that a number of predictor variables had large \(p\)-values suggesting we do not need to include all of them. Indeed, including unnecessary predictor variables can inflate the variance of parameter estimates, which can have a negative impact on predictive performance. For illustration, suppose we refit the model, omitting a few of the predictor variables that seem less important:
## Fit model using only age, chol and weight as predictors
summary(glm(y ~ age + chol + weight, data=chapman, family="binomial"))##
## Call:
## glm(formula = y ~ age + chol + weight, family = "binomial", data = chapman)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.1049 -0.5541 -0.3777 -0.2510 2.7009
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -9.255892 2.071678 -4.468 0.0000079 ***
## age 0.053004 0.020827 2.545 0.0109 *
## chol 0.006518 0.003589 1.816 0.0693 .
## weight 0.017539 0.008272 2.120 0.0340 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 154.55 on 199 degrees of freedom
## Residual deviance: 135.52 on 196 degrees of freedom
## AIC: 143.52
##
## Number of Fisher Scoring iterations: 5Now there are no coefficients with large \(p\)-values. We can estimate the test error for this reduced model as follows:
## Fit reduced logistic regression model to training data:
lr_red_train = glm(y ~ age + chol + weight, data=chapman[train_set,],
family="binomial")
## Compute fitted values for the validation data:
phat_red_test = predict(lr_red_train, chapman[!train_set,], type="response")
yhat_red_test = ifelse(phat_red_test > 0.5, 1, 0)
## Compute test error:
1 - mean(chapman$y[!train_set] == yhat_red_test)## [1] 0.1376147We note that this is smaller than the test error for the full model, in agreement with our intuition.
5.3.2 Example: MBA Admissions Data Continued Again
Implementing the validation set approach for LDA and QDA using the lda and qda functions from the MASS package is very similar to the approach taken for logistic regression using the glm function. Again, we begin by sampling the indices for our training and validation data as follows:
## Sample indices of training data:
train_set = sample(c(TRUE, FALSE), nrow(admission), replace=TRUE)Then we can build the classifier using the training data and calculate the predicted values for the validation data:
## Train Bayes classifier for LDA using the training data
lda_train = lda(decision ~ ., data=admission[train_set,])
## Compute predicted values for the validation data:
lda_test = predict(lda_train, admission[!train_set,])
yhat_test = lda_test$classNow we can produce the (test) confusion matrix by cross-tabulating the observed and fitted values:
## Calculate confusion matrix:
(confusion = table(Observed=admission$decision[!train_set], Predicted=yhat_test))## Predicted
## Observed admit border notadmit
## admit 10 1 0
## border 1 14 0
## notadmit 0 2 16Finally we compute the test error:
1 - mean(admission$decision[!train_set] == yhat_test)## [1] 0.09090909Note that the test error is larger than the training error we computed in Section 5.2.2, as expected.
5.3.3 Example: Banknote Authentication Data
At the beginning of the chapter, we motivated the study of classification problems using the banknote authentication data set which contains data extracted from digitized images of notes that were known to be either forged or genuine. These data were collected to provide a way of automatically categorising new banknotes whose status (forged or genuine) was not yet known, using information extracted from a digitized image.
We begin by loading the data from the durhamSLR package and printing the first few rows:
## Load the banknote authentication data:
data(banknotes)
## Examine the data:
head(banknotes)table(banknotes[,5])##
## 0 1
## 762 610In this case the data comprise a random sample of 762 forged banknotes and a random sample of 610 genuine banknotes. However, we do not have a random sample of notes – the actual proportion of forged banknotes in circulation is not greater than 50%! Strictly speaking, this means it is not appropriate to use logistic regression because our sample is not “representative” in the way described. However, we can use LDA or QDA if we have independently derived estimates of these probabilities. We will therefore focus on LDA and QDA and compare the performance of the two methods by calculating the test error rate in each case.
We will use the validation set approach and hence begin by sampling the indices for our training and validation data as follows:
## Sample indices of training data:
train_set = sample(c(TRUE, FALSE), nrow(banknotes), replace=TRUE)Next we use the lda function to estimate the parameters in the model underpinning LDA based on the training data:
## Perform LDA:
lda(class ~ ., data=banknotes[train_set,])## Call:
## lda(class ~ ., data = banknotes[train_set, ])
##
## Prior probabilities of groups:
## 0 1
## 0.5770925 0.4229075
##
## Group means:
## variance skewness kurtosis entropy
## 0 2.357594 3.8509645 1.010301 -0.9806932
## 1 -1.852207 -0.6458102 1.861539 -1.4355944
##
## Coefficients of linear discriminants:
## LD1
## variance -0.84477073
## skewness -0.45351646
## kurtosis -0.59775819
## entropy -0.03548854As remarked in Section 4.6, by default the lda and qda functions estimate the prior group membership probabilities using the sample proportions. As discussed above, this is not appropriate for these data. However, suppose it is known that around one in five hundred banknotes are forged. Then we could estimate the group membership probabilities by \(\hat{\pi}_1=0.002\) and \(\hat{\pi}_2=0.998\). These probabilities can be passed to the lda function using the prior argument as follows:
## Perform LDA on the training data:
(lda_train = lda(class ~ ., data=banknotes[train_set,], prior=c(0.002, 0.998)))## Call:
## lda(class ~ ., data = banknotes[train_set, ], prior = c(0.002,
## 0.998))
##
## Prior probabilities of groups:
## 0 1
## 0.002 0.998
##
## Group means:
## variance skewness kurtosis entropy
## 0 2.357594 3.8509645 1.010301 -0.9806932
## 1 -1.852207 -0.6458102 1.861539 -1.4355944
##
## Coefficients of linear discriminants:
## LD1
## variance -0.84477073
## skewness -0.45351646
## kurtosis -0.59775819
## entropy -0.03548854Next we compute the fitted values for the validation data using the predict function
## Compute fitted values for the validation data:
lda_test = predict(lda_train, banknotes[!train_set,])
yhat_test = lda_test$classAnd finally we compute the test error
1 - mean(banknotes$class[!train_set] == yhat_test)## [1] 0.06657019We can now repeat this procedure to compute the test error using QDA:
## Perform QDA on the training data:
(qda_train = qda(class ~ ., data=banknotes[train_set,], prior=c(0.002, 0.998)))## Call:
## qda(class ~ ., data = banknotes[train_set, ], prior = c(0.002,
## 0.998))
##
## Prior probabilities of groups:
## 0 1
## 0.002 0.998
##
## Group means:
## variance skewness kurtosis entropy
## 0 2.357594 3.8509645 1.010301 -0.9806932
## 1 -1.852207 -0.6458102 1.861539 -1.4355944## Compute fitted values for the validation data:
qda_test = predict(qda_train, banknotes[!train_set,])
yhat_test = qda_test$class
## Compute test error:
1 - mean(banknotes$class[!train_set] == yhat_test)## [1] 0.04196816The test error rate appears to be lower under QDA with which we would be able to automatically classify around 96% of banknotes correctly.