Variable Selection and Resampling Methods

Download Lecture-Workshop Notes for Week 3

1 Introduction to Variable Selection

1.1 Motivating Example – Prostate Cancer Data

Prostate cancer is the most common cancer in men in the UK. Fortunately, cure rates are high. One treatment option is surgery (called a radical prostatectomy) which aims to remove the whole prostate and the prostate cancer cells inside it. Prostate-specific antigen (PSA) is a protein made by both normal and cancerous prostate cells. It can be elevated in cases of prostate cancer and other prostate problems.

Throughout this chapter, we will use as a running example a data set that came come from a study that examined the relationship between the level of PSA and 8 clinical measures (e.g. age, prostate weight) in 97 men with prostate cancer who were about to receive a radical prostatectomy.

The data are arranged into a \(n \times p\) array with

• \(n=97\) rows corresponding to the men;
• \(p=9\) columns corresponding to the variables: the level of PSA and the 8 clinical measures.

The data are available from the ElemStatLearn package. Unfortunately, this package is no longer hosted on CRAN so it must be installed from source. After downloading the file ElemStatLearn_2015.6.26.2.tar.gz from Ultra, save it in a directory of your choice. The package can then be installed in RStudio by going to Tools then Install Packages. In the pop-up box that appears, change the drop-down option for “Install from:” to “Package Archive File (.tar.gz)”. Then navigate to the file ElemStatLearn_2015.6.26.2.tar.gz and click Open. Finally click Install.

Once ElemStatLearn has been installed, we can load the package and data set in the usual way:

## Load R package:
library(ElemStatLearn)
## Load data into R:
data(prostate)
## Print the first 5 rows:
head(prostate, 5)

Our response variable is the log PSA, lpsa, in column 9. Columns 1 to 8 contain the 8 clinical measures which will serve as our predictor variables. Note that the final column, column 10, is not of interest for now and we will remove it:

ProstateData = prostate[,-10]
## Store the number observations and number of predictors:
n = nrow(ProstateData); p = ncol(ProstateData) - 1

To get a feel for the relationships among the predictor variables and between the predictor variables and the response variable, we can produce a scatterplot matrix, as you saw towards the end of last week:

pairs(ProstateData)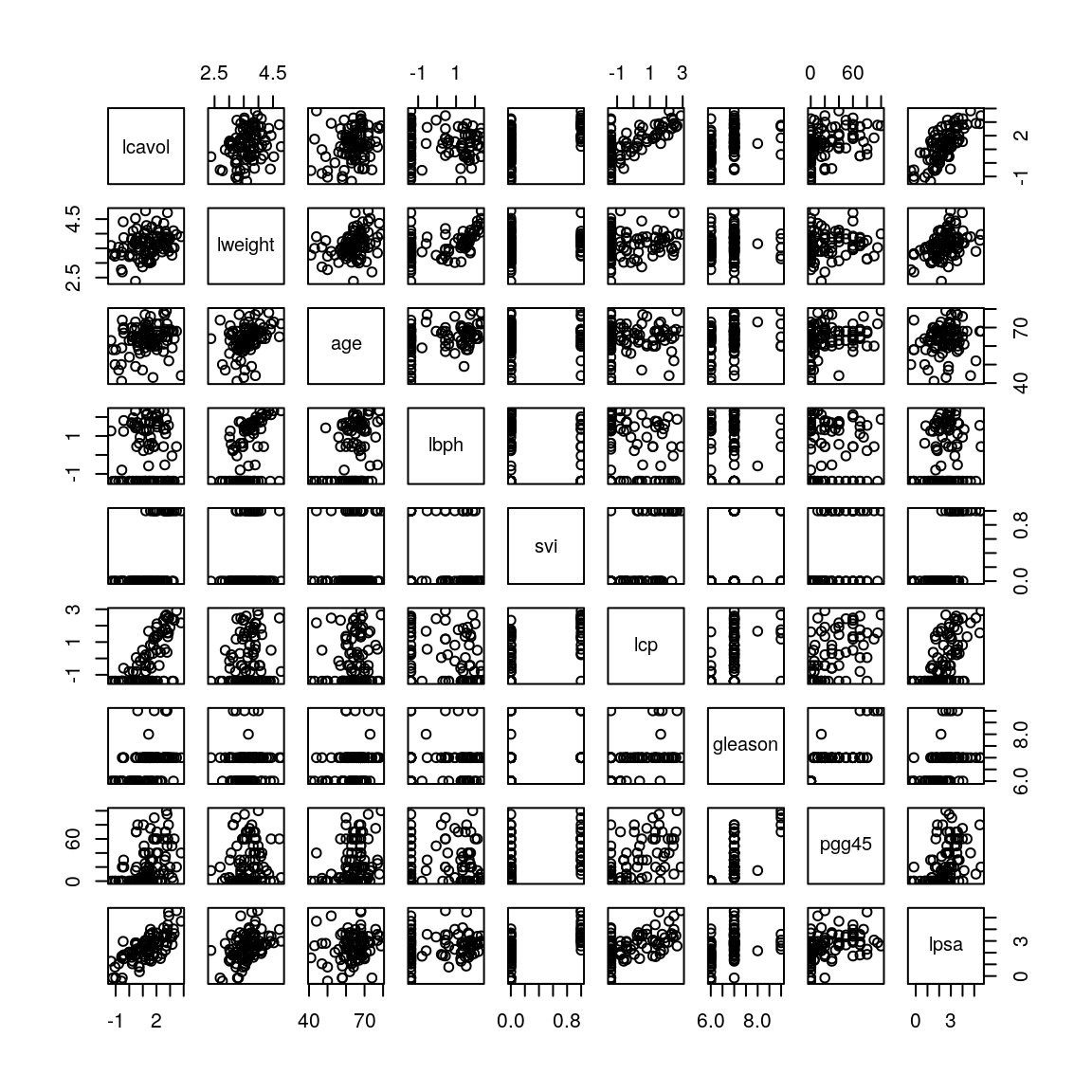

Figure 1.1: Scatterplot matrix for prostate cancer data.

This produces the plot in Figure 1.1. Focusing on the bottom row where lpsa is plotted on the \(y\)-axis, we see some variables, like lcavol have a strong (positive) linear relationship with lpsa while for other variables, like age, the (positive) linear relationship is much weaker. If we now focus on column 5 where svi is plotted on the \(x\)-axis we see that svi can only take two possible values – 0 and 1. Similarly, if we look at column 7 where gleason is plotted on the \(x\)-axis, we see that there are only four values for gleason represented in these data – 6, 7, 8 and 9. We can confirm these observations using the unique function which returns the unique elements in a vector:

## Possible values for svi:
unique(prostate$svi)

## [1] 0 1

## Possible values for gleason:
unique(prostate$gleason)

## [1] 6 7 8 9

In fact, svi is a categorical variable with two possible values, which we normally refer to as its “levels”, indicating whether or not the seminal vesicles have been invaded by prostate cancer. The variable gleason is an ordered categorical variable which, for cancers, has five possible levels labelled 6, 7, 8, 9 and 10, with larger values indicating more aggressive cancer. Note from the R output above that we do not observe any patient with a gleason score of 10 in this data set.

As discussed in the “Dummy Variables” video in Workshop 5, we can incorporate a categorical predictor variable with \(k\) levels by introducing \(k-1\) dummy or indicator variables. For svi we can therefore choose “no seminal invasion” as the baseline and introduce an invasion indicator variable \(x_{5}\) defined through: \[\begin{equation*} x_{5} = \begin{cases} 1, \quad &\text{if seminal invasion observed;}\\ 0, \quad &\text{otherwise.} \end{cases} \end{equation*}\] If we look at the output of unique(prostate$svi) above, we see that svi has already been encoded as an indicator variable. In principle we could proceed in a similar fashion for gleason, choosing level 6 as the baseline and introducing four indicator variables – one for each of levels 7 to 10. However, gleason is an ordered categorical variable and so, in this case, we would expect lpsa to only increase or only decrease as the gleason level goes up. Indeed, if we look at the \((9,7)\)-panel in Figure 1.1, we see that there is a weak (positive) linear relationship between gleason and lpsa. Therefore we can reasonably treat the gleason level as a quantitative variable. This leads to a simpler model because it means we have only a single explanatory variable representing the effect of gleason and not four. We will therefore leave \(x_{7}\) as it is. Consequently the first 8 columns of ProstateData can be used as our predictor variables with no pre-processing.

As seen in the previous part of the course, we can fit a multiple linear regression model using the lm function:

## Fit linear model:
lsq_fit = lm(lpsa ~ ., data=ProstateData)
## Summarise model fit:
summary(lsq_fit)

## 
## Call:
## lm(formula = lpsa ~ ., data = ProstateData)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.76644 -0.35510 -0.00328  0.38087  1.55770 
## 
## Coefficients:
##              Estimate Std. Error t value      Pr(>|t|)    
## (Intercept)  0.181561   1.320568   0.137       0.89096    
## lcavol       0.564341   0.087833   6.425 0.00000000655 ***
## lweight      0.622020   0.200897   3.096       0.00263 ** 
## age         -0.021248   0.011084  -1.917       0.05848 .  
## lbph         0.096713   0.057913   1.670       0.09848 .  
## svi          0.761673   0.241176   3.158       0.00218 ** 
## lcp         -0.106051   0.089868  -1.180       0.24115    
## gleason      0.049228   0.155341   0.317       0.75207    
## pgg45        0.004458   0.004365   1.021       0.31000    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6995 on 88 degrees of freedom
## Multiple R-squared:  0.6634, Adjusted R-squared:  0.6328 
## F-statistic: 21.68 on 8 and 88 DF,  p-value: < 0.00000000000000022

Notice that the syntax lpsa ~ . means that lpsa is the response variable and it is regressed on all other columns in the ProstateData data frame, i.e. all other columns are taken as predictor variables. Examining the output of the summary function we see that the coefficient of determination is given by \(R^2=0.6634\). We interpret this to mean that 66.34% of the variation in log PSA can be explained by regression on the eight predictors. This leaves a relatively large proportion of the variation unexplained, i.e. attributed to random error. Inspecting the coefficient table, we see that, conditional on inclusion of all other predictor variables, the \(t\)-tests: \[\begin{equation*} H_0: \beta_i = 0 \quad \text{versus} \quad H_1: \beta_i \ne 0 \end{equation*}\] for age, lbph, lcp, gleason and pgg45 all have large \(p\)-values. This suggests that if we consider them one a time, each of these predictors contributes little to a model that already contains the other seven predictor variables. Therefore we are unlikely to need to include all of them.

But why might we want to get rid of some predictor variables? There are a number of reasons:

• To improve predictive performance: Suppose the model is fitted using least squares, which is the technique introduced in the first half of this module. Typically when we have a large number of predictors (\(p\)) relative to the number of observations (\(n\)) we can’t estimate their coefficients very precisely using least squares and so the variance of the least squares estimator is large. Recall that the variance of the least squares estimator tells us how much our estimates would vary if we could repeatedly take samples from the population regression model and recompute the least squares estimates. When the variance is large this means our estimates of the regression coefficients would vary widely. Consequently, so too would our predictions from the fitted model using future data that were not used in model-fitting. This corresponds to poor predictive performance.
• To improve model interpretability: A model with fewer predictors is easier to interpret and use for generating predictions using future data. It can therefore be helpful to eliminate predictor variables which are not associated with the response given the other predictors in the model.

There are classic methods for deciding on how to eliminate sets of predictors, for example, by applying the extra sum of squares principle. In this module we will consider a method called best-subset selection which belongs to a general class of techniques called variable selection or feature selection methods.

1.2 Best-Subset Selection

The main idea behind variable selection methods is that if we can identify a “good” subset of \(p^{\ast}<p\) predictor variables, then we can learn the effects of our (reduced set of) predictor variables more precisely. This reduces the variance in our parameter estimates and can therefore improve predictive performance.

As its name suggests, best subset selection involves using least squares to fit a linear regression model to each possible subset of the \(p\) explanatory variables. So we would fit the so-called null model with no predictors (i.e. just an intercept), all \(p\) models with a single predictor, all \(p(p-1)/2\) models with two predictors, and so on. It turns out that if we continue in this fashion there are \(2^p\) possible models. We compare all of them to decide which one is “best”. The full procedure is as follows:

1. Fit the null model, \(\mathcal{M}_0\), which contains no predictor variables, and is simply \(\hat{y} = \bar{y}\).
2. For \(k=1,2,\ldots,p\):
   1. Fit all \(\binom{p}{k}\) models that contain exactly \(k\) predictor variables.
   2. Select the model amongst these which has the smallest residual sum of squares \(SSE\), or equivalently, the largest coefficient of determination \(R^2\). Call this model \(\mathcal{M}_k\).
3. Select a single “best” model from amongst \(\mathcal{M}_0, \mathcal{M}_1, \ldots, \mathcal{M}_p\).

To compare linear models which contain the same number of predictor variables, we can simply use the coefficient of determination \(R^2\), selecting the model which maximises this statistic. This is what we do in step 2(b) above. However, in step 3, when comparing models with different numbers of predictor variables, if we were to pick the one which maximised \(R^2\), we would always select \(\mathcal{M}_p\), which contains all the predictors. This is because \(R^2\) cannot decrease as predictor variables are added to the model. To get around this problem, a few alternative statistics have been proposed to compare models with different numbers of predictor variables. They all work by trading off terms which reward good model-fit (typically based on \(R^2\) or \(SSE\)) with terms that penalise model complexity. For a model with \(k\) predictors we can compute, for example:

• Adjusted \(R^2\): defined by
  \[\begin{equation*} R^2_{\text{adj}} = 1 - (1 - R^2) \frac{n - 1}{n - k - 1} \end{equation*}\] which adjusts \(R^2\) to penalise model complexity (i.e. large \(k\)). We would choose the model for which \(R^2_{\text{adj}}\) is largest.
• Mallow’s \(C_p\) statistic: equal to \(SSE / n\) plus a penalty for model complexity. We would choose the model for which \(C_p\) is smallest.
• Bayes Information Criterion (BIC): equal to \(SSE / n\) plus a (different) penalty for model complexity. The penalty for BIC tends to penalise models with lots of explanatory variables more heavily than the penalty for Mallow’s \(C_p\) statistic and so often favours simpler models. We would choose the model for which BIC is smallest.

Another option is to use \(k\)-fold cross-validation to pick the number of predictors. The general method is introduced in Section 3.3 and its use in this context is explored in computer labs.

In practice, the different statistics often suggest different models are “best” and so it is usually a good idea to consider more than one measure and look for some sort of consensus.

1.2.1 Example: Prostate Cancer Data Continued

Consider again the prostate cancer data which we examined in Section 1.1. We are going to use R to apply the best subset selection approach. To do this we will use the regsubsets function from the leaps package. We begin by loading the package:

library(leaps)

Then we apply the regsubsets function. The syntax is almost identical to that for the lm function except we should also specify that we want to use best subset regression by setting the method argument equal to "exhaustive". Also, we need to use the nvmax argument to specify the size of the largest subset we wish to consider. In general this should be the number of predictors, \(p\).

bss = regsubsets(lpsa ~ ., data=ProstateData, method="exhaustive", nvmax=p)

By applying the summary function to the returned object, we can see which models were identified as \(\mathcal{M}_1, \ldots, \mathcal{M}_8\):

(bss_summary = summary(bss))

## Subset selection object
## Call: regsubsets.formula(lpsa ~ ., data = ProstateData, method = "exhaustive", 
##     nvmax = p)
## 8 Variables  (and intercept)
##         Forced in Forced out
## lcavol      FALSE      FALSE
## lweight     FALSE      FALSE
## age         FALSE      FALSE
## lbph        FALSE      FALSE
## svi         FALSE      FALSE
## lcp         FALSE      FALSE
## gleason     FALSE      FALSE
## pgg45       FALSE      FALSE
## 1 subsets of each size up to 8
## Selection Algorithm: exhaustive
##          lcavol lweight age lbph svi lcp gleason pgg45
## 1  ( 1 ) "*"    " "     " " " "  " " " " " "     " "  
## 2  ( 1 ) "*"    "*"     " " " "  " " " " " "     " "  
## 3  ( 1 ) "*"    "*"     " " " "  "*" " " " "     " "  
## 4  ( 1 ) "*"    "*"     " " "*"  "*" " " " "     " "  
## 5  ( 1 ) "*"    "*"     "*" "*"  "*" " " " "     " "  
## 6  ( 1 ) "*"    "*"     "*" "*"  "*" " " " "     "*"  
## 7  ( 1 ) "*"    "*"     "*" "*"  "*" "*" " "     "*"  
## 8  ( 1 ) "*"    "*"     "*" "*"  "*" "*" "*"     "*"

In the above output the asterisk indicates that a variable is included in the model. So, for example, the best model with one predictor variable, \(\mathcal{M}_1\), uses lcavol; the best model with two predictor variables, \(\mathcal{M}_2\), uses lcavol and lweight; and so on.

In addition to the output printed to the screen, the summary function also computes a number of statistics to help us choose the best overall model. This includes the three discussed above: adjusted \(R^2\), Mallow’s \(C_p\) statistic and the BIC which can be accessed as follows:

## Adjusted Rsq:
bss_summary$adjr2

## [1] 0.5345839 0.5868977 0.6242063 0.6280585 0.6335279 0.6349654 0.6365002 0.6327886

## Mallow's Cp statistic:
bss_summary$cp

## [1] 27.406210 14.747299  6.173546  6.185065  5.816804  6.466493  7.100428  9.000000

## BIC:
bss_summary$bic

## [1] -66.05416 -74.07188 -79.71614 -77.18955 -75.11192 -71.99028 -68.90809 -64.44401

The optimal value of \(k\) in each case is therefore:

(best_adjr2 = which.max(bss_summary$adjr2))

## [1] 7

(best_cp = which.min(bss_summary$cp))

## [1] 5

(best_bic = which.min(bss_summary$bic))

## [1] 3

To help us decide on the “best” model, we can assess graphically how each statistic varies with the number of predictor variables \(k\) via:

## Create multi-panel plotting device:
par(mfrow=c(1,3))
## Produce plots, highlighting optimal value of k:
plot(1:8, bss_summary$adjr2, xlab="Number of predictors", ylab="Adjusted Rsq", 
     type="b")
points(best_adjr2, bss_summary$adjr2[best_adjr2], col="red", pch=16)
plot(1:8, bss_summary$cp, xlab="Number of predictors", ylab="Cp", type="b")
points(best_cp, bss_summary$cp[best_cp], col="red", pch=16)
plot(1:8, bss_summary$bic, xlab="Number of predictors", ylab="BIC", type="b")
points(best_bic, bss_summary$bic[best_bic], col="red", pch=16)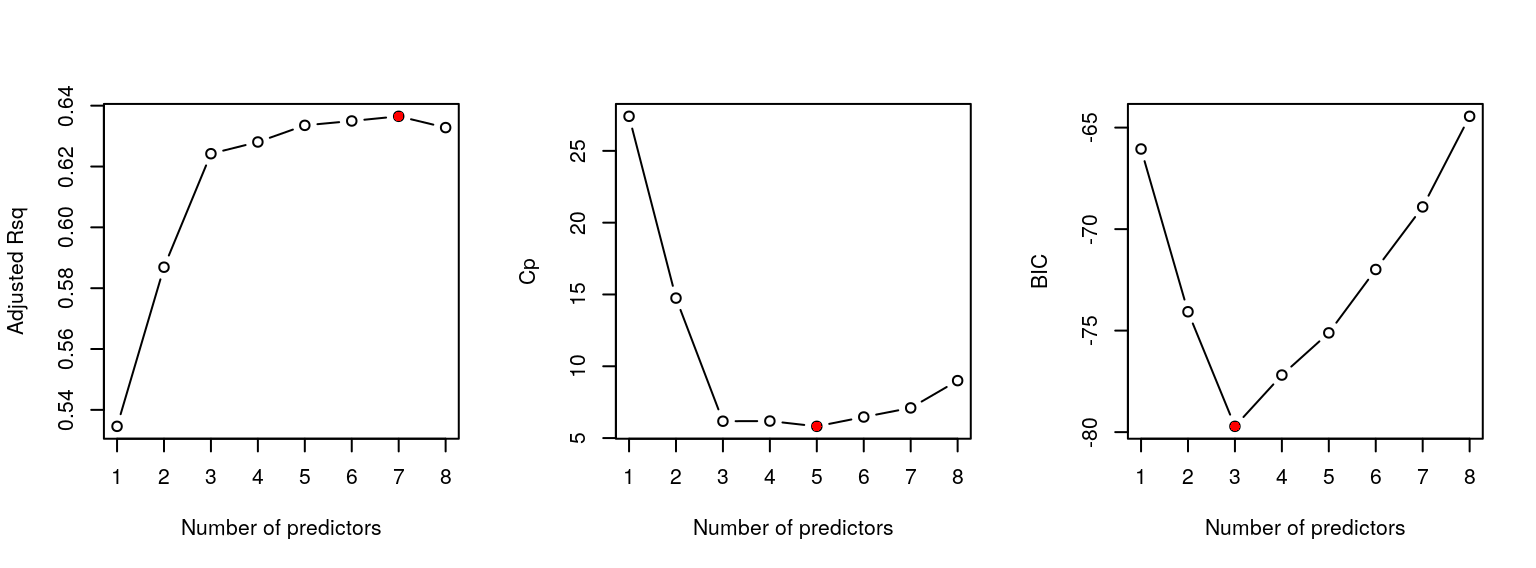

Figure 1.2: Best subset selection for the prostate cancer data.

which generates the plot in Figure 1.2.

Unfortunately, as very often occurs in practice, the different methods select different models. Adjusted \(R^2\) suggests \(\mathcal{M}_7\), whilst Mallow’s \(C_p\) statistic and the BIC suggest \(\mathcal{M}_5\) and \(\mathcal{M}_3\), respectively. However, if we examine the plot for adjusted \(R^2\), it suggests there is little difference between models \(\mathcal{M}_3, \ldots, \mathcal{M}_8\), whilst the plot for Mallow’s \(C_p\) statistic suggests there is little difference between models \(\mathcal{M}_3, \ldots, \mathcal{M}_7\). Therefore we might regard the best model as \(\mathcal{M}_3\) (which includes lcavol, lweight and svi).

In order to obtain the least squares estimates of the coefficients for one of the models, say, \(\mathcal{M}_3\), we can use the coef function:

coef(bss, 3)

## (Intercept)      lcavol     lweight         svi 
##  -0.7771566   0.5258519   0.6617699   0.6656666

where the second argument refers to the number of explanatory variables \(k\) in the model of interest \(\mathcal{M}_k\).

Although conceptually appealing, the main problem with best-subset selection is that the number of models to be considered grows very fast with the number of predictor variables \(p\). For example, for the prostate cancer data we had \(p=8\) predictor variables leading to \(2^p = 2^8 = 256\) possible models. If \(p=16\), we would have needed to consider \(65 \, 536\) models, and if \(p=32\), then there would have been over four billion! As a result, best subset selection becomes computationally infeasible for values of \(p\) greater than around 40. You will study other techniques that are more appropriate when \(p\) is large (or large relative to \(n\)) in the Machine Learning module.

2 Assessing Predictive Error

A popular approach for assessing and comparing supervised learning techniques, which is particularly popular in the machine learning literature, is to base the judgement on their predictive performance. In other words on the extent to which the predicted value of an “output” variable for a particular individual / item matches the value we actually observe. In this week’s lecture-workshops we will consider application of these ideas in the context of linear regression models. Next week, we will consider their application in the context of classification methods where we have a categorical, rather than quantitative, “output” variable, e.g. disease status.

In judging the predictive performance of a supervised learning method, we need to distinguish between two kinds of error:

• Test error: the average error that results from predicting the response for an observation that was not used in model-fitting. This is sometimes called out-of-sample validation. The data used in model-fitting are called training data. The data used to assess the predictive performance are called validation data or test data.
• Training error: the average error that results from predicting the response for an observation that was used in model-fitting. This is called in-sample validation and uses only training data.

It is generally easier to perform in-sample validation because we use the same data to fit and validate the model. In a regression context, common measures of the training error include the residual sum of squares \(SSE\) or, equivalently, the coefficient of determination \(R^2\). However, the most commonly presented measure of training error is the average mean squared error (MSE) over the training data: \[\begin{equation*} MSE = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \frac{1}{n} SSE \end{equation*}\] where the fitted value \(\hat{y}_i\) is given by \[\begin{equation*} \hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_{i1} + \ldots + \hat{\beta}_p x_{ip}, \qquad \text{for $i=1,\ldots,n$.} \end{equation*}\] For example, we can compute the training error associated with the 3-predictor model identified in Section 1.2.1 as follows:

## Fit the three-predictor model:
lsq_fit_3 = lm(lpsa ~ lcavol + lweight + svi, data=ProstateData)
## Compute fitted values:
yhat = predict(lsq_fit_3, ProstateData)
head(yhat)

##         1         2         3         4         5         6 
## 0.7506893 0.8968425 0.7352084 0.7621830 1.8894181 0.8075323

## Compute training error:
training_error = mean((ProstateData$lpsa - yhat)^2)
training_error

## [1] 0.480087

Although easy to compute, we’re typically not very interested in the training error. What we’re really interested in is the test error because this measures how well the method performs on previously unseen data and is therefore a more faithful characterisation of the model’s predictive performance. Unfortunately, the training error is typically an underestimate of the test error, essentially due to its double-use of the data for constructing and testing the model. The test error can be estimated in a number of ways. In the context of linear regression, the methods we considered in the previous section for comparing models with different numbers of predictors – adjusted \(R^2\), Mallow’s \(C_p\) statistic and the BIC – can be regarded as measures of test error; they work by making a mathematical adjustment to the training error rate so that it estimates the test error rate. However, a more common method for estimating the test error, which works more generally for all regression and classification methods, is a class of resampling methods called cross-validation. This is the subject of the following section.

3 Cross-Validation

3.1 The Validation Set Approach

Before introducing the cross-validation approach, we will consider a simpler out-of-sample validation method called the validation set approach. The idea is to split the data into two: the training data and the validation (or test) data. The training data is used to estimate the model parameters to give the fitted model. Then the test data is used to compute the test error. For ease of explanation, suppose we are fitting a simple linear regression model: \[\begin{equation*} Y = \beta_0 + \beta_1 x + \epsilon. \end{equation*}\] Suppose further that our training data comprise \((x_1, y_1), \ldots, (x_{n_1}, y_{n_1})\) where \(n_1 < n\) and that our test data comprise \((x_{n_1+1}, y_{n_1+1}), \ldots, (x_n, y_{n})\). By fitting the model using the training data, we obtain estimates \(\hat{\beta}_0\) and \(\hat{\beta}_1\) of the regression coefficients, and then make predictions over the test set using \[\begin{equation*} \hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_{i}, \qquad \text{for $i=n_1+1,\ldots,n$.} \end{equation*}\] Finally, we estimate the test mean-squared-error (\(MSE\)) with \[\begin{equation*} VS = \frac{1}{n-n_1} \sum_{i=n_1+1}^n (y_i - \hat{y}_i)^2 \end{equation*}\] in which \(n-n_1\) is the number of observations in the test set.

For our prostate cancer data, for example, we could sample our training and test sets as follows:

## Set the seed to make the analysis reproducible
set.seed(1)
## Randomly sample a set of indices for the training data
train_set = sample(c(TRUE, FALSE), n, replace=TRUE)
## Print first 9 elements
head(train_set, 9)

## [1]  TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE FALSE

## Deduce indices of test data
test_set = !train_set

So the indices for the training data are the positions where we have TRUE in train_set and the indices for the test data are the positions where we have a FALSE in train_set and hence a TRUE in test_set:

head(which(train_set==TRUE)) ## or, more concisely: head(which(train_set))

## [1] 1 3 4 6 7 8

head(which(test_set==TRUE))  ## or, more concisely: head(which(test_set))

## [1]  2  5  9 10 16 17

We now estimate the test error by fitting the model to the training data and calculating the fitted values for the test data. We begin by considering the full model with 8 predictors:

## Fit full model using training data
lsq_train = lm(lpsa ~ ., data=ProstateData[train_set,])
## Compute fitted values for test data:
yhat_test = predict(lsq_train, ProstateData[test_set,])
head(yhat_test)

##         2         5         9        10        16        17 
## 0.4616526 1.4987918 0.8332913 1.0875066 1.7511600 1.1634700

## Compute test error
test_error = mean((ProstateData[test_set,]$lpsa - yhat_test)^2)
test_error

## [1] 0.6992266

Repeating this procedure for the 3-predictor model identified in Section 1.2.1 we find

## Fit 3-predictor model using training data
lsq_train_3 = lm(lpsa ~ lcavol + lweight + svi, data=ProstateData[train_set,])
## Compute fitted values for test data:
yhat_test_3 = predict(lsq_train_3, ProstateData[test_set,])
## Compute test error
test_error_3 = mean((ProstateData[test_set,]$lpsa - yhat_test_3)^2)
test_error_3

## [1] 0.6014814

The test error for the 3-predictor model is lower than that for the full model, indicating better predictive performance. This is as expected since the model comparison criteria we considered previously, like adjusted-\(R^2\), are also intended to measure test error and they suggested the 3-predictor model was better than the full model. Note that we use the same split of the data into training and validation sets for the 3-predictor model and full model to make the comparison as fair as possible.

Although straightforward to implement, the validation set approach suffers from two drawbacks:

1. If we repeat this procedure using a different split of the data, we will get different results. For example, consider the 3-predictor model where our previous estimate of the test error was 0.6014814:

## Sample a new set of training and test indices
train_set = sample(c(TRUE, FALSE), n, replace=TRUE)
test_set = !train_set
## Fit 3-predictor model using training data
lsq_train_3 = lm(lpsa ~ lcavol + lweight + svi, data=ProstateData[train_set,])
## Compute fitted values for test data
yhat_test_3 = predict(lsq_train_3, ProstateData[test_set,])
## Compute test error
test_error_3 = mean((ProstateData[test_set,]$lpsa - yhat_test_3)^2)
test_error_3

## [1] 0.572272

       Sometimes the test error rate can vary substantially between splits which makes it difficult to draw conclusions.

2. Only a subset of the observations are being used to fit the model which might make its performance appear unduly poor, i.e. the test error is overestimated.

We can address these problems using another out-of-sample validation approach called cross-validation. We will consider two variants in the following sections.

3.2 Leave-One-Out Cross-Validation

Leave-one-out cross-validation (LOOCV) is similar to the validation set approach in that it involves splitting the observations into two parts. However, this splitting procedure is now performed \(n\) times. For ease of explanation, suppose we are, again, fitting a simple linear regression model. The first split takes the single observation \((x_1, y_1)\) as the test data and the remaining \(n-1\) observations as training data: \((x_2, y_2), \ldots, (x_n, y_n)\). After fitting the model using the training data, we make a prediction \(\hat{y}_1\) over the test set and then estimate the test error with \[\begin{equation*} MSE_1 = (y_1 - \hat{y}_1)^2. \end{equation*}\] Next, we repeat the procedure taking \((x_2, y_2)\) as our test data and the remaining \(n-1\) observations as our training data: \((x_1, y_1), (x_3, y_3), \ldots, (x_n, y_n)\). This yields our second estimate of the test error as \[\begin{equation*} MSE_2 = (y_2 - \hat{y}_2)^2. \end{equation*}\] Repeating this procedure \(n\) times generates \(n\) estimates of the test error: \(MSE_1, MSE_2, \ldots, MSE_n\) which are averaged to produced the overall LOOCV estimate of the test \(MSE\): \[\begin{equation*} CV_{(n)} = \frac{1}{n} \sum_{i=1}^n MSE_i. \end{equation*}\]

For example, in the prostate cancer example, we can write some code to produce the LOOCV estimate of the test \(MSE\) for our full model as follows:

## Create a vector to store the test error estimates:
test_errors = numeric(n)
## Estimate the test MSE based on all n splits of the data:
for(i in 1:n) {
  ## Fit the model using the training data:
  lsq_train = lm(lpsa ~ ., data=ProstateData[-i,])
  ## Compute fitted values over the test set:
  yhat_test = predict(lsq_train, ProstateData[i,])
  ## Compute estimate of MSE
  test_errors[i] = (yhat_test - ProstateData[i,]$lpsa)^2
}
## Average MSE_1, ..., MSE_n to produce the overall estimate of test MSE:
(LOOCV = mean(test_errors))

## [1] 0.5413291

Repeating this for our 3-predictor model yields:

## Create a vector to store the test error estimates:
test_errors_3 = numeric(n)
## Estimate the test MSE based on all n splits of the data:
for(i in 1:n) {
  ## Fit the model using the training data:
  lsq_train = lm(lpsa ~ lcavol + lweight + svi, data=ProstateData[-i,])
  ## Compute fitted values over the test set:
  yhat_test = predict(lsq_train, ProstateData[i,])
  ## Compute estimate of MSE
  test_errors_3[i] = (yhat_test - ProstateData[i,]$lpsa)^2
}
## Average MSE_1, ..., MSE_n to produce the overall estimate of test MSE:
(LOOCV_3 = mean(test_errors_3))

## [1] 0.5255275

Again, the test error estimated using LOOCV suggests the 3-predictor model is better than the full model.

The main advantage of LOOCV over the validation-set approach is that each set of training data contains \(n-1\) observations and so we typically estimate the regression coefficients more precisely than we did in the validation-set approach where our (single) training set was smaller. This means we can typically estimate the test error with less bias, i.e. it tends to be less of an overestimate.

However, there are two major disadvantages with LOOCV:

1. It can be computationally expensive to implement because we have to fit the model \(n\) times. Obviously, this will be a problem if \(n\) is large or if each individual model is slow to fit. For some supervised learning methods, the time taken to fit an individual model can take minutes, hours, or even days, which can render LOOCV computationally infeasible. (Linear regression can actually be regarded as an exception here. Although we will not dwell on the mathematical details and did not use it above, there is actually a formula for \(CV_{(n)}\) which makes the cost of calculating the LOOCV estimate of the test error the same as that of a single model-fit. However, it does not work for other supervised learning methods and so we will not consider it further.)

2. As a method of estimating the test error, LOOCV has a high variance. This is because the \(n\) training sets used to generate the \(n\) estimates of the test error are almost identical and so these individual estimates are highly positively correlated.

We can address both of these limitations using another cross-validation method called \(k\)-fold cross-validation.

3.3 \(k\)-fold Cross-Validation

In \(k\)-fold cross validation we randomly divide the data into \(k\) groups or folds of approximately equal size. The last \(k-1\) folds are used as the training data then the first fold is used as a test set. We compute the test error rate based on this first fold. The process is then repeated using the second fold as the test set, then the third fold, and so on.

Eventually this procedure gives us \(k\) estimates of the test error rate which are averaged to give the overall test error. In linear regression, for example, we would obtain \(k\) estimates of the test mean-squared error \(MSE_1, \ldots, MSE_k\) and then compute the overall \(k\)-fold cross-validation estimate of the test MSE through \[\begin{equation*} CV_{(k)} = \frac{1}{k} \sum_{i=1}^k MSE_i. \end{equation*}\] It should be clear that LOOCV is a special case of \(k\)-fold cross-validation when \(k=n\). However, typical choices for the number of folds are \(k=5\) or \(k=10\) and not \(k=n\). Why is this? First, there are significant computational benefits to choosing \(k\) to be a reasonably small number like \(k=5\) or \(k=10\), namely that this only requires fitting the model to the data \(5\) or \(10\) times, respectively. This can often be computationally feasible in cases when LOOCV is not.

In addition to this computational benefit, there are also mathematical arguments to suggest that \(k\)-fold cross validation with \(k=5\) or \(k=10\) can lead to more accurate estimates of the test error than LOOCV. As explained in the previous section, the \(n\) estimates of the test error in LOOCV tend to be highly correlated because the \(n\) training data sets are almost identical. The overlap between training sets is substantially smaller for \(k\)-fold cross-validation and so the \(k\) estimates of the test error tend to be less positively correlated. The mean of highly correlated quantities has a higher variance than the mean of quantities that are less highly correlated and so the the method of estimating the test error using LOOCV tends to have a higher variance than the method of estimating the test error using \(k\)-fold cross-validation. On the other hand, because each training set in \(k\)-fold cross-validation contains fewer observations than each training set in LOOCV, for each split of the data, \(k\)-fold cross validation can produce slightly biased estimates of the test error.

The choice of \(k\) in \(k\)-fold cross-validation is therefore said to be a bias-variance-trade-off. There is some empirical evidence to suggest that the choices \(k=5\) or \(k=10\) yield estimates of the test error that suffer neither from excessively high bias nor from very high variance.

In the computer labs we will write our own R code to perform \(k\)-fold cross-validation for linear regression models. We will also use it as an alternative to the statistics proposed in Section 1.2 for choosing the number of predictors \(0,1,\ldots,p\) during best subset selection.

4 The Bootstrap

4.1 Key Ideas

Cross-validation, considered in the previous section, is an example of a method from a broader class of techniques called resampling methods. These methods involve repeatedly drawing samples from a training set and refitting a model of interest to each sample in order to obtain additional information about the fitted model. Another example of a resampling technique is the bootstrap.

The bootstrap is a method for estimating standard errors, confidence intervals, and other measures of uncertainty for a wide variety of problems. The key idea is to resample from the original data to create replicate datasets, from which the variability of the quantities of interest can be assessed, without the need to perform analytical calculation.

The basic bootstrap algorithm can be summarized as follows:

1. Start with a sample \(S\) of size \(n\).
2. Draw a sample of size \(n\) with replacement from \(S\). This is called a bootstrap sample. (With replacement means that when an observation is drawn from the sample, it is returned to the sample before another draw is made. As such, any given observation may be sampled more than once).
3. Repeat step 2 \(B\) times (\(B\) large).
4. Calculate the statistic of interest (e.g. mean, median, variance) for each bootstrap sample – this is called a bootstrap replication of the statistic of interest.
5. Investigate the approximate sampling distribution of the statistic using the \(B\) bootstrap replications you computed in 4.

Let’s start with a simulated dataset as an example, we will take a sample of size 100 from the standard normal distribution, i.e. the normal distribution with mean 0 and variance 1.

## Set the seed to make the analysis reproducible:
set.seed(1)
## Generate a sample of size 100 from the standard normal distribution:
n = 100
vec = rnorm(n)
## Calculate the mean and variance:
mean(vec)

## [1] 0.1088874

var(vec)

## [1] 0.8067621

We compute the mean and the variance of our sample and obtain 0.1089 and 0.8068 respectively. Our sample estimates are not very close to the population values of 0 and 1, but, if we were to compute confidence intervals for the population mean and population variance, both intervals would be quite wide. Let’s look at the 95% confidence interval for the population mean. In the first part of the module, we saw that if we have a sample from a normal population with unknown population parameters, we can calculate a 95% confidence intervals for the population mean using the formula: \[\begin{equation} \bar{x} \pm t_{n-1,0.025} (s / \sqrt{n}) \tag{4.1} \end{equation}\] where \(n\) is the sample size, \(\bar{x}\) is the sample mean, \(s\) is the sample standard deviation and the term in parentheses (\(s / \sqrt{n}\)) is our estimate of the standard error of the sample mean. In R, we have

xbar = mean(vec)
s = sd(vec)
(std_err = s / sqrt(n))

## [1] 0.08981994

tval = qt(1-0.025, df=99)

## [1] -0.06933487  0.28710961

Now let’s try to apply the bootstrap process described above. We will set \(B=1000\) here. We will take \(1000\) bootstrap samples of size 100 with replacement from our vector vec, calculate their means and variances, and store the output to bmeans and bvars respectively.

## Set number of bootstrap samples:
B = 1000
## Set up vectors to store the bootstrap replications of the sample mean and variance:
bmeans = numeric(B)
bvars = numeric(B)
for (b in 1:B){
  ## Draw bootstrap sample:
  bsample = sample(vec, 100, replace=TRUE)
  ## Calculate bootstrap replications:
  bmeans[b] = mean(bsample)
  bvars[b] = var(bsample)
}

Making a histogram of the bootstrap replications of the sample mean:

hist(bmeans, main="")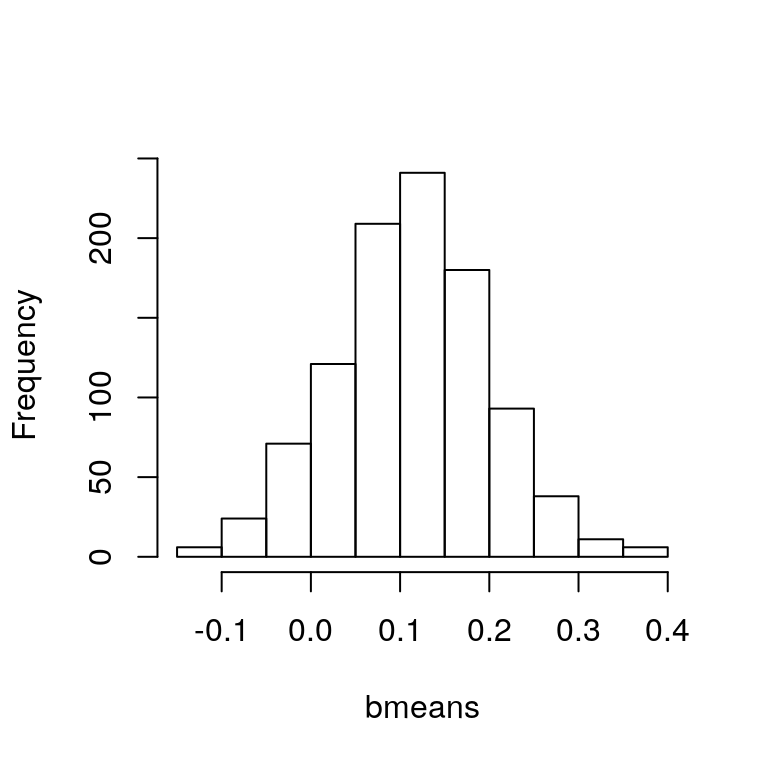

Figure 4.1: Histogram of bootstrapped sample means.

yields the plot in Figure 4.1. Computing their standard deviation gives the bootstrap estimate of the standard error of the sample mean estimator:

sd(bmeans)

## [1] 0.08645806

which is very close to the value we calculated above using the direct formula \(s / \sqrt{n}\). Similarly, we can make a histogram of the bootstrap replications of the sample variance:

hist(bvars, main="")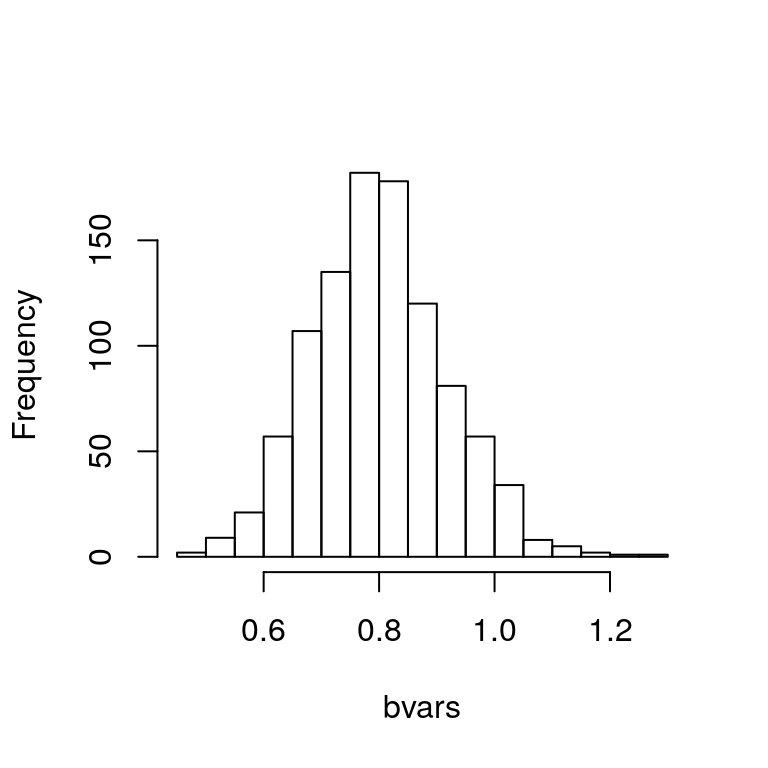

Figure 4.2: Histogram of bootstrapped sample variances.

which yields the plot in Figure 4.2.

If we compute the 2.5% and 97.5% percentiles from bmeans, we can produce an approximation of the 95% confidence interval for the population mean that we produced earlier:

quantile(bmeans, c(0.025, 0.975))

##        2.5%       97.5% 
## -0.05815818  0.27701803

which is very close to our confidence interval that was derived using the direct formula (4.1). Bootstrapping is particularly useful for cases where deriving a formula for the confidence interval is difficult or impossible. In the case of the population variance, we saw in the first part of the course that we can use a Chi-squared distribution to compute a 95% confidence interval. Alternatively, we could produce an estimate using our bootstrap replications of the sample variance:

quantile(bvars, c(0.025, 0.975))

##     2.5%    97.5% 
## 0.587580 1.024373

The computations we have carried out so far can be reproduced using the boot function from the R package of the same name. The function has three arguments:

1. The original data stored as a vector, matrix or data frame. (If the data are stored in a matrix or data frame then each row is considered as one multivariate observation).
2. A function which returns a vector containing the statistic(s) of interest. This function should have two arguments: the data and a vector of indices that define the bootstrap sample.
3. The number of bootstrap samples to be drawn, i.e. \(B\).

This is best understood in the context of an example. To calculate the bootstrap replications of the sample mean and variance for our vector vec we proceed as follows:

## Load the boot package:
library(boot)
## Define functions for calculating the statistics of interest:
samplemean = function(x, d){
  return(mean(x[d]))
}
samplevar = function(x, d){
  return(var(x[d]))
}
## Use the boot function to create the bootstrap replications:
(bootMean = boot(vec, samplemean, B))

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = vec, statistic = samplemean, R = B)
## 
## 
## Bootstrap Statistics :
##      original      bias    std. error
## t1* 0.1088874 0.002525678   0.0862961

(bootVar = boot(vec, samplevar, B))

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = vec, statistic = samplevar, R = B)
## 
## 
## Bootstrap Statistics :
##      original       bias    std. error
## t1* 0.8067621 -0.009308139    0.114134

We can then generate confidence intervals, for example 95% confidence intervals using:

boot.ci(bootMean, type="basic", conf = 0.95)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bootMean, conf = 0.95, type = "basic")
## 
## Intervals : 
## Level      Basic         
## 95%   (-0.0545,  0.2685 )  
## Calculations and Intervals on Original Scale

boot.ci(bootVar, type="basic", conf = 0.95)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bootVar, conf = 0.95, type = "basic")
## 
## Intervals : 
## Level      Basic         
## 95%   ( 0.5799,  1.0288 )  
## Calculations and Intervals on Original Scale

4.2 Estimating the Accuracy of a Linear Regression Model

The bootstrap approach can also be used to assess the variability of the coefficient estimates and predictions from a statistical learning method. Here we use the bootstrap approach in order to assess the variability of the estimates for \(\beta_0\) and \(\beta_1\), the intercept and slope terms, for a linear regression model that uses lcavol to predict lpsa in the prostate cancer data set. In the first half of the module, formulae for the variances of \(\hat{\beta}_0\) and \(\hat{\beta}_1\) were presented. Taking square roots gives the standard errors of \(\hat{\beta}_0\) and \(\hat{\beta}_1\). We will compare the estimates obtained using the bootstrap to those obtained using these formulae.

We first create a simple function, boot.fn, which takes in the data as well as a set of indices for the observations, and returns the coefficient estimates for the linear regression model. We then apply this function to the full set of n=97 observations in order to compute the estimates of \(\beta_0\) and \(\beta_1\) from the entire data set using the usual lm function you have seen previously:

boot.fn = function(Xy, index) {
  ## Make sure the response variable is called y:
  colnames(Xy)[ncol(Xy)] = "y"
  ## Fit the model:
  lsq_fit = lm(y ~ ., data=Xy[index,])
  ## Extract and return the estimated coefficients:
  return(coef(lsq_fit))
}
n = nrow(ProstateData)
boot.fn(ProstateData[, c("lcavol", "lpsa")], 1:n)

## (Intercept)      lcavol 
##   1.5072975   0.7193204

boot.fn function can also be used to create bootstrap estimates for the intercept and slope terms by randomly sampling from among the observations with replacement. Here we give two examples.

set.seed(1)
boot.fn(ProstateData[, c("lcavol", "lpsa")], sample(n, n, replace=TRUE))

## (Intercept)      lcavol 
##   1.4650652   0.7760488

boot.fn(ProstateData[, c("lcavol", "lpsa")], sample(n, n, replace=TRUE))

## (Intercept)      lcavol 
##   1.4916758   0.7174135

Next, we use the boot function to compute the standard errors of 1000 bootstrap estimates for the intercept and slope terms.

(bootCoefs = boot(ProstateData[, c("lcavol", "lpsa")], boot.fn, 1000))

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = ProstateData[, c("lcavol", "lpsa")], statistic = boot.fn, 
##     R = 1000)
## 
## 
## Bootstrap Statistics :
##      original       bias    std. error
## t1* 1.5072975 -0.002533400  0.12644541
## t2* 0.7193204  0.001322689  0.07636109

We can then use the boot.ci function to compute confidence intervals for the intercept (index=1) and slope (index=2)

## 95% confidence interval for the intercept
boot.ci(bootCoefs, type="basic", conf = 0.95, index=1)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bootCoefs, conf = 0.95, type = "basic", index = 1)
## 
## Intervals : 
## Level      Basic         
## 95%   ( 1.262,  1.776 )  
## Calculations and Intervals on Original Scale

## 95% confidence interval for the slope
boot.ci(bootCoefs, type="basic", conf = 0.95, index=2)

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = bootCoefs, conf = 0.95, type = "basic", index = 2)
## 
## Intervals : 
## Level      Basic         
## 95%   ( 0.5739,  0.8741 )  
## Calculations and Intervals on Original Scale

This indicates that the bootstrap estimate for the standard error of \(\hat{\beta}_0\) is 0.1264, with 95% confidence interval \((1.262, 1.776)\), and that the bootstrap estimate for standard error of \(\hat{\beta}_1\) is 0.0764, with 95% confidence interval \((0.5739, 0.8741)\). If instead we use the standard formulae to compute the standard errors and confidence intervals for the regression coefficients in a linear model, we get:

lsq_fit = lm(lpsa ~ lcavol, data=ProstateData)
summary(lsq_fit)$coef

##              Estimate Std. Error  t value                      Pr(>|t|)
## (Intercept) 1.5072975 0.12193685 12.36130 0.000000000000000000001722289
## lcavol      0.7193204 0.06819289 10.54832 0.000000000000000011186085585

confint(lsq_fit)

##                 2.5 %    97.5 %
## (Intercept) 1.2652222 1.7493727
## lcavol      0.5839404 0.8547004

The standard error estimates for \(\hat{\beta}_0\) and \(\hat{\beta}_1\) obtained using the standard formulas are 0.1219 for the intercept, with 95% confidence interval \((1.2652, 1.7494)\), and 0.0682 for the slope, with 95% confidence interval \((0.5839, 0.8547)\). These are somewhat different from the estimates obtained using the bootstrap. Does this indicate a problem with the bootstrap? In fact, it suggests the opposite.

The standard formulae for computing the standard errors for regression coefficients rely on certain assumptions. For example, they depend on the unknown error standard deviation \(\sqrt{\text{Var}(\epsilon)}=\sigma\). We then estimate \(\sigma\) using the residual standard error \(s_e\). Now, although the formulae for the standard errors do not rely on the linearity assumption that underpins the regression model being correct, the estimate for \(\sigma\) does. Similarly, the assumptions underpinning the formulae for confidence intervals for regression coefficients rely on the assumption that the errors \(\epsilon\) have a normal distribution. Let us investigate whether there is any evidence to contradict the model assumptions using the regression diagnostics you saw earlier in the module:

## Make multipanel plotting device
par(mfrow=c(1,2))
## Plot regression diagnostics
plot(lsq_fit, which=1)
plot(lsq_fit, which=2)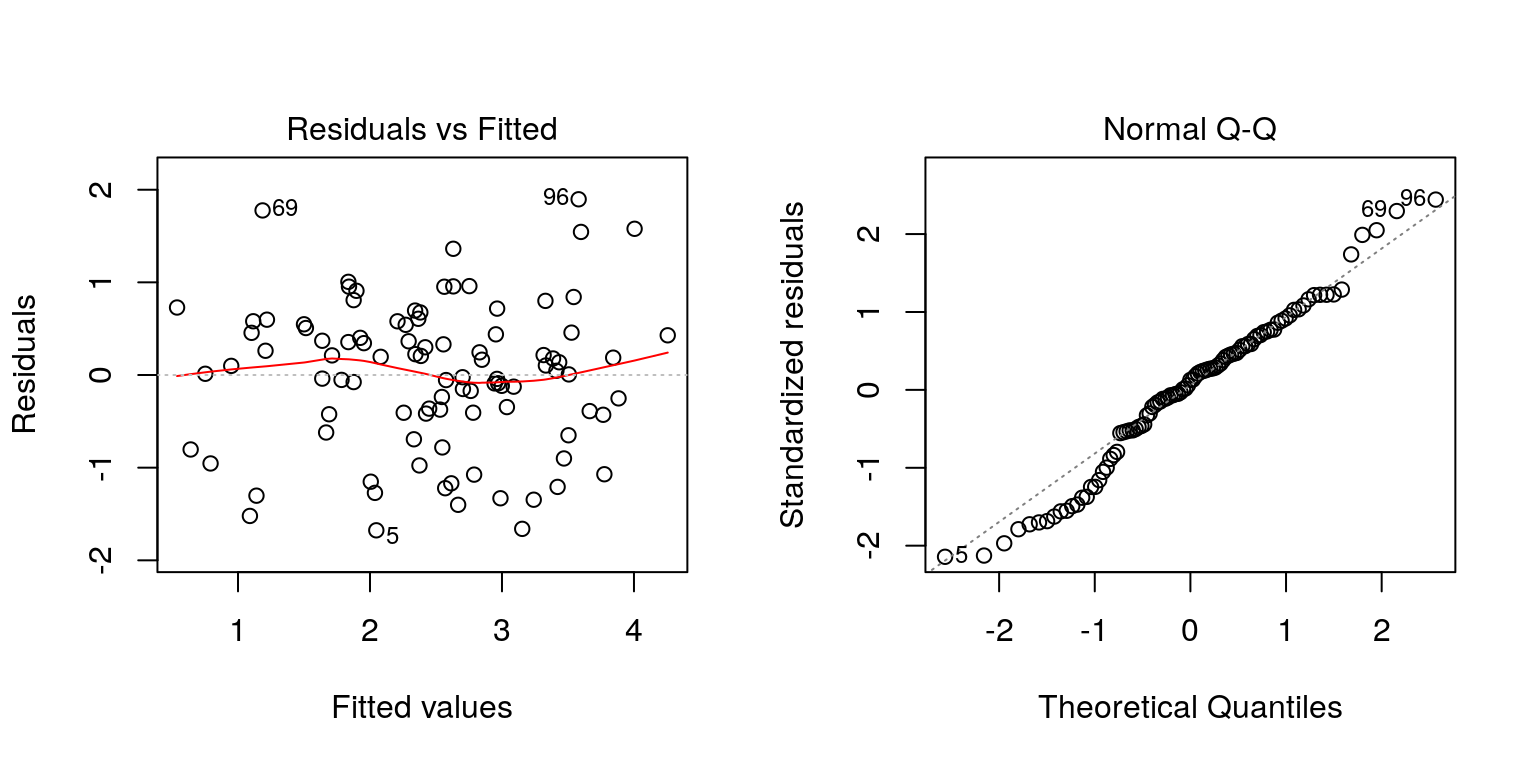

Figure 4.3: Regression diagnostic plots.

This yields the plot in Figure 4.3. The plot of the residuals against the fitted values shows random scatter and so does not suggest any problems with the linearity assumption of the model or the assumption of equal variance of the error terms. However, the normal quantile plot shows substantial deviations from the best-fitting line in the upper right and lower left corners, indicating the assumption of normality is questionable. The bootstrap approach does not rely on these normality assumptions, and so it is likely giving a more accurate estimate of the confidence intervals for \(\hat{\beta}_0\) and \(\hat{\beta}_0\) than the standard formulae.